meetkunde problemen 6 t/m 10

vorige volgende

6.



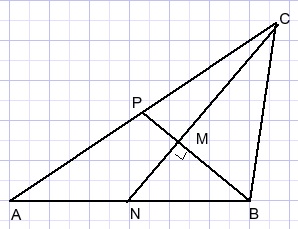
AB = 6; AC = 8
BP en CN zijn zwaartelijnen en staan loodrecht op elkaar.

Opgave: bereken BC.



7.



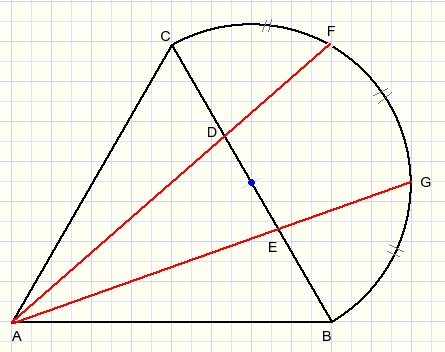
Gegeven:
Gelijkzijdige driehoek ABC .
M is het middelpunt van BC en van een halve cirkelboog.
De bogen CF, FG en GB zijn gelijk.
Te bewijzen:
CD = DE = EB.



8.



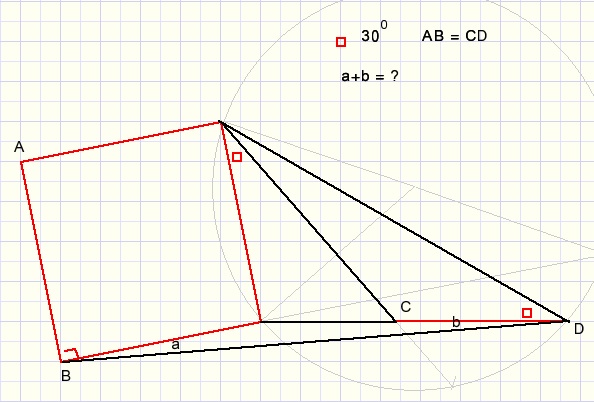
Gegeven is een vierkant en lijnstuk CD = AB.
De met een rood rechthoekje aangegeven hoeken zijn 300
Gevraagd wordt de hoeken a+b te berekenen.



9.
Gegeven zijn punten A en B en cirkel c.
Construeer een cirkel door A en B die c snijdt in diametraal tegengestelde punten.



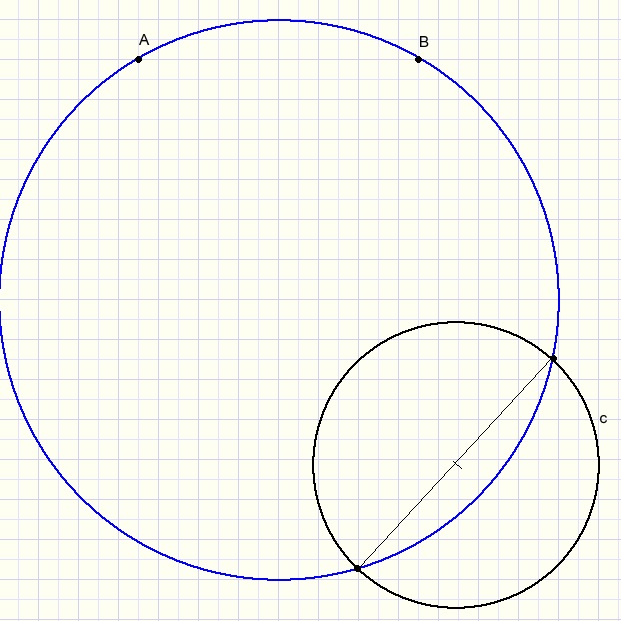
(In de tekening hierboven is de blauwe cirkel de oplossing)



10.



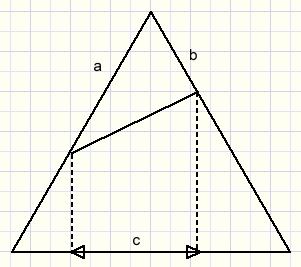
We zien een gelijkzijdige driehoek.
Te bewijzen is dat:
    a + b = 2c




volgende