

| Een meetkunde puzzel (9) |  |
Deze meetkunde puzzel werd 14-09-2018 op facebook geplaatst door Tungsteno.
De oplossing is van mijzelf.
Gegeven zijn punten A en B en cirkel c.
Construeer een cirkel door A en B die c snijdt in diametraal tegengestelde punten.
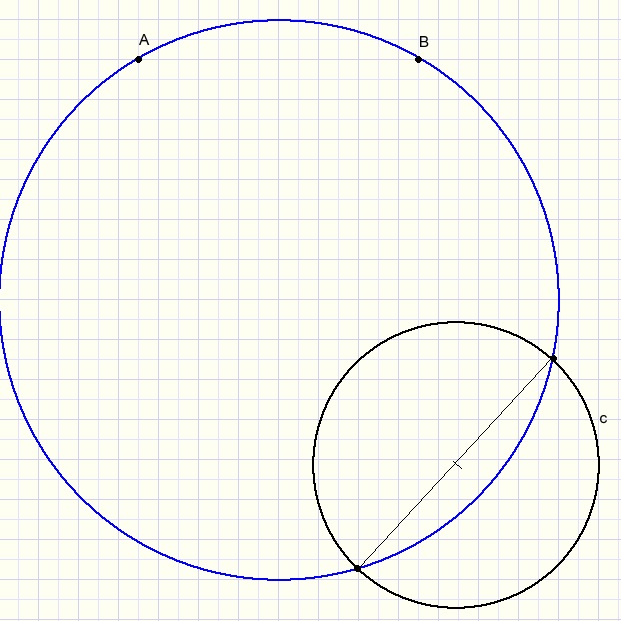
In de tekening hierboven is de blauwe cirkel de oplossing.
Bekijk nu het volgende plaatje:
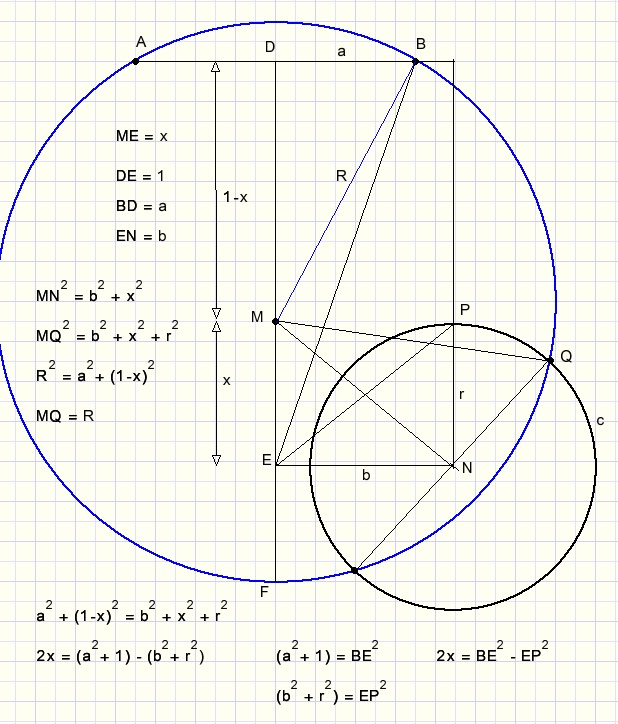
Middelpunt N van cirkel c stellen we op afstand 1 van lijn AB.
Middelpunt M van de te construeren cirkel moet op de middelloodlijn van AB liggen.
Punt N heeft afstand b tot deze middelloodlijn.
Dus: 2x= BE2 - EP2.
We gaan verder:
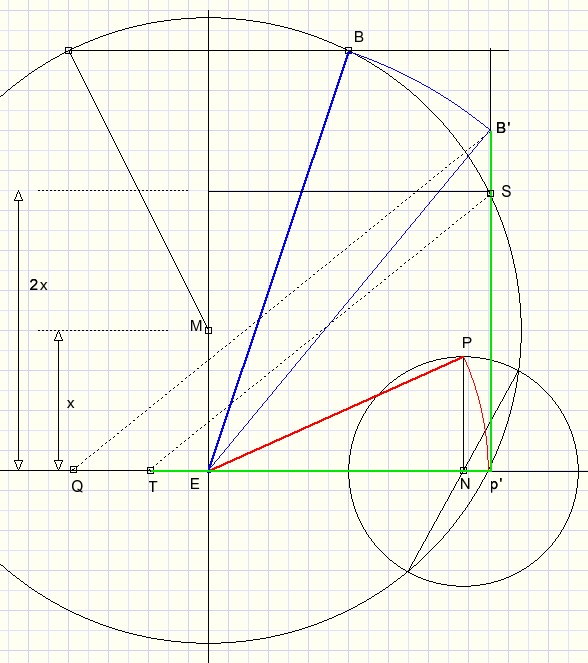
Neem E als middelpunt.
Cirkel EP om naar EP'
Teken lijn vanuit P' loodrecht op EN.
Cirkel EB om , B' is het snijpunt met voorgaande lijn vanuit P'.
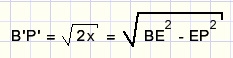
Nu moet voorgaande formule nog gekwadrateerd worden om 2x te verkrijgen.
Verleng P'E zo, dat P'Q = 1.
Teken P'T = P'B'
Teken TS parallel aan QB'.
P'S = 2x
Opmerking:

Zo te zien ligt punt S op cirkel M.
Is dit toeval?
Nee, dat is het niet.
Het bewijs laat ik over aan de lezer.
Hiermee besluit ik de oplossing van dit fraaie meetkunde probleem.
Hoewel.....
Het leuke van meetkunde is dat er met logisch redeneren enorm veel rekenwerk kan worden vermeden.
Bij de oplossing van voorgaand probleem paste ik alleen wat basisregels van de meetkunde toe wat een
hoop aanvullende algebra vereiste.
Wat extra denkwerk leverde later het inzicht om de oplossing met alleen meetkunde te bereiken.
Dat vergt wel de toepassing van een krachtige stelling.
Eerst dus die stelling met het bewijs.
Neem eens 1 punt A en een cirkel.
Dan zijn er heel veel cirkels te tekenen die door dat punt A gaan
en de cirkel snijden in diagonaal liggende punten (P and Q).
(kies steeds P en Q anders)
Zie het volgende plaatje:
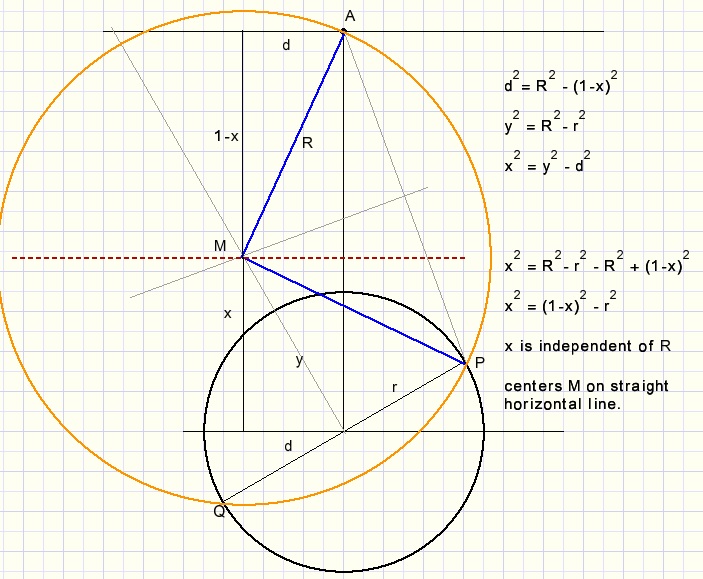
We nemen aan dat A afstand 1 heeft tot het middelpunt van de cirkel met P en Q.
Het blijkt dat x onafhankelijk is van straal R van de cirkel door A,P,Q.
De middelpunten M liggen dus allemaal op een rechte lijn, die loodrecht op AN moet staan.
De nieuwe stelling luidt:
-
De middelpunten van alle cirkels die door een punt gaan en een andere cirkel
snijden in diametraal gelegen punten, liggen op een rechte lijn.
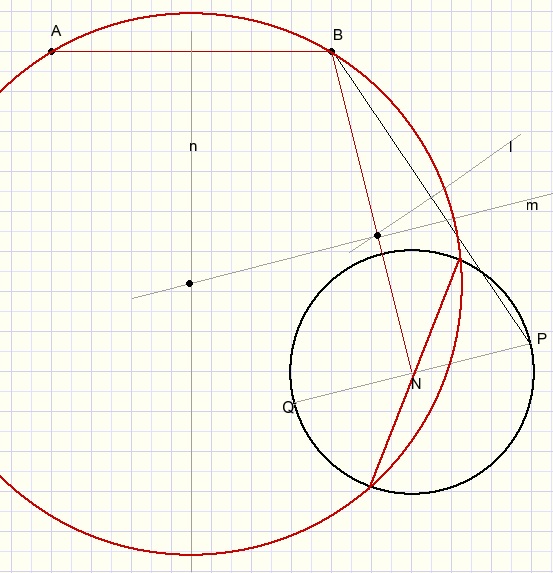
- teken BN.
- teken PQ loodrecht op BN.
- teken BP.
- teken lijn l , middelloodlijn van BP.
- teken lijn m door het snijpunt van l en BN, parallel aan PQ.
- teken lijn n, middelloodlijn van AB
- middelpunt M van de gevraagde cirkel is het snijpunt van m en n.
Opmerking: lijn m bestaat uit alle middelpunten van cikels door punten B, P en Q.
(als P en Q verdraaien)
Lijn n bestaat uit alle middelpunten van de cirkels door A en B.

