

| Meetkunde puzzel (7) |  |
De volgende meetkunde puzzel is van Omid Motahed, docent wiskunde in Beijing.
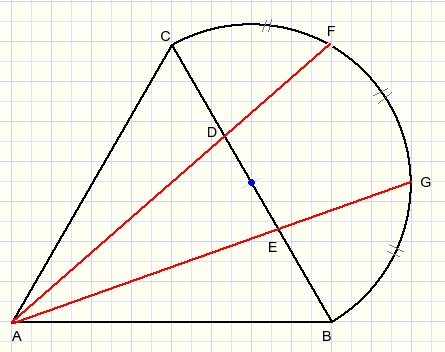
Gegeven:
Gelijkzijdige driehoek ABC .
M is het middelpunt van BC en van een halve cirkelboog.
De bogen CF, FG en GB zijn gelijk.
Te bewijzen:
CD = DE = EB.
Bewijs:
Wegens symmetrie geldt: CD = EB.
Verleng lijnstukken AB en FG, snijpunt is H.
Trek lijnstukken FM, MG, GB.
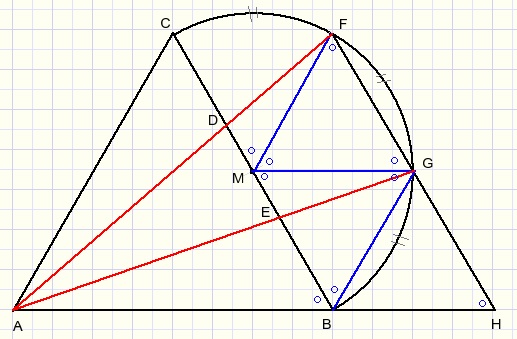
LFMG = 600.....zesde deel van 3600
FM = GM, dus LMFG = LMGF = 600
Evenzo:
LGMB=LMGB=LGBM=600.
LBGH=1800-600-600= 600
Daaruit volgt:
FH||BC..............(1)
Driehoeken FMG en BMG zijn gelijkzijdig met gemeenschappelijke zijde MG.
Driehoeken BMG en BHG zijn gelijkzijdig met gemeenschappelijke zijde BG.
Daarom is: FG = GH............(2)
(1) en (2) gecombineerd:
DE = EB
Toelichting
Wegens gelijkvormigheid van driehoeken ADE en AFG geldt:
DE / FG = AE / AG
Wegens gelijkvormigheid van driehoeken AEB en AGH geldt:
EB / GH = AE / AG = EB / FG

