

| meetkunde problemen 1 t/m 5 |  |
1.
Hieronder staat getekend een vierkant met vier overlappende cirkelsegmenten.
De hoekpunten zijn de middens van de cirkelbogen.
De afmetingen van het vierkant zijn 1 * 1.
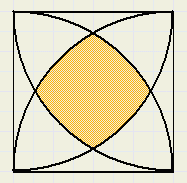
Bereken de oppervlakte van het middelste (gekleurde) deel.
Laat in het antwoord de constante π en wortels staan.
2.
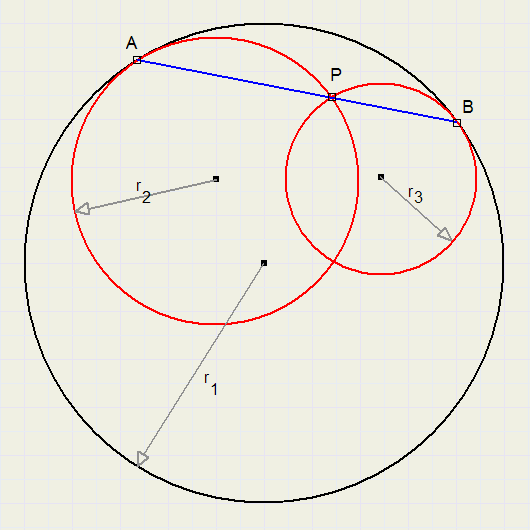
Gegeven is een cirkel met straal r1 met daarbinnen twee inwendig rakende cirkels met straal r2 en r3
Van elke cirkel is ook het middelpunt bekend.
Punten A en B zijn de raakpunten van cirkels 2 en 3 aan cirkel 1.
P is het snijpunt van cirkels 2 en 3.
bewijs dat:
Als P op de lijn AB ligt, dan moet gelden : r1 = r2 + r3
3.
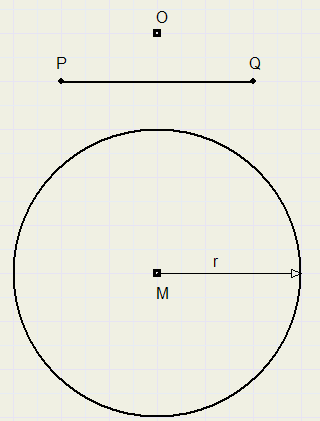
Gegeven zijn een cirkel met straal r en middelpunt M,
een punt O buiten de cirkel en een lijnstuk PQ < 2r
Gevraagd:
Construeer een lijn door O, die de cirkel snijdt in de punten R en S zo, dat RS = PQ
4.
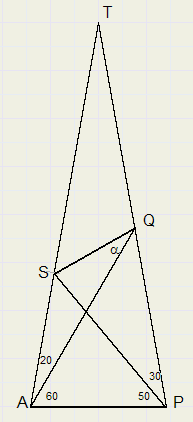
Gegeven is deze driehoek met de aangegeven hoeken.
Gevraagd wordt de grootte van hoek α .
Er mag alleen gebruik worden gemaakt van meetkunde, geen goniometrie of vectormeetkunde.
5.
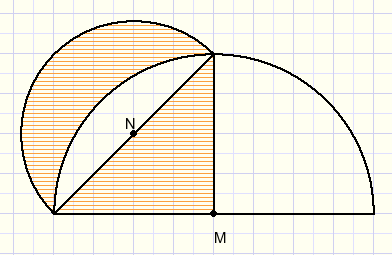
De twee cirkelbogen hebben M,N als middelpunten.
Bewijs dat de gearceerde oppervlakten gelijk zijn.

