|
 |
Meetkunde Puzzel + 3 oplossingen |
 |
 |
Opgave
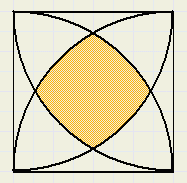
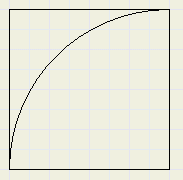
Hieronder staat getekend een vierkant met vier overlappende cirkelsegmenten.
De hoekpunten zijn de middens van de cirkelbogen.
De afmetingen van het vierkant zijn 1 * 1.
Bereken de oppervlakte van het middelste (gekleurde) deel.
Laat in het antwoord de constante p en wortels staan.
Oplossing 1.
We schieten met kanonnen op muggen en gebruiken de integraalrekening.
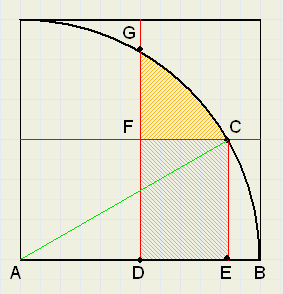
Een kwart van de gevraagde oppervlakte is het gebied FCG, dat gelijk is aan
gebied DECG - DECF.
Met de oorsprong in A is de functie van de cirkelboog:
Nu is AD =
En AE =
zodat: (verschil boven- en ondergrens, AE - AD)
oppervlakte DECG =
oppervlakte DECG = + · − − · =
met
DE = −
FD =
is
oppervlakte DECF = −
zodat oppervlakte gebied FCG = − +
en het oorspronkelijk te berekenen gebied is het viervoudige:
Oplossing 2.
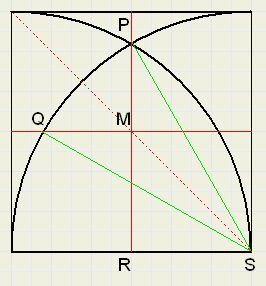
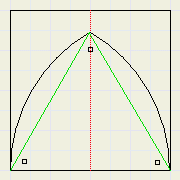
Bekijk de figuur hieronder:
LRSM = 450
LRSP = 600, want P en S vormen gelijkzijdige driehoek met hoekpunt linksonder
zodat
LMSP = 150
LQSP = 300
De oppervlakte van cirkelsegment QSP = p =
Oppervlakte DMSP = 0,5*PM * RS
met RS =
.....en PM = −
......is
oppervlakte DMSP = −
en
oppervlakte DMSP + DMSQ = −
Een kwart van de gevraagde oppervlakte is nu
De gehele oppervlakte, omsloten door de 4 cirkelbogen:
Oplossing 3.
(oplossing E.C.Buissant des Amorie)
 |
 |
 |
| 4x+4y+z=1 |
2x+3y+z=
|
x+2y+z=2 · − |
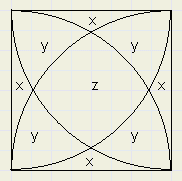
Opmerking : in de rechter figuur is
...de oppervlakte van de gelijkzijdige driehoek.
Deze is dubbel gerekend bij optelling van de cirkelsegmenten.
Het volgende stelsel vergelijkingen moet dus worden opgelost:
| | | x + 2 y + z = −
2 x + 3 y + z =
4 x + 4 y + z = 1 | | |
Regel (1) *4 , regel (3)*-1 en optellen:
Regel (2)*2, regel (3)*-1 en optellen:
| | | 4 y + 3 z = p − − 1
2 y + z = | | |
Nu regel (2)*-2 en optellen:

|
|