meetkunde probleem

Gegeven zijn een cirkel met straal r en middelpunt M,
een punt O buiten de cirkel en een lijnstuk PQ < 2r

Gevraagd:
Construeer een lijn door O, die de cirkel snijdt in de punten R en S zo, dat RS = PQ

Oplossing 1 (van mijzelf)

Teken de cirkel (M,MO)........................{cirkel met middelpunt M en straal MO}
Trek de lijn door M en O.
Deze lijn snijdt cirkel(M,r) in het punt T.
Cirkel de afstand PQ om vanuit T, snijpunt met cirkel(M,r) is U.........{TU = PQ}
Verleng het lijnstuk TU, snijpunten met cirkel(M,MO) zijn V en W.
Cirkel de afstand VO om vanuit W, snijpunt met cirkel(M,MO) is X.
Trek de lijn door O en X, deze snijdt cirkel(M,r) in Y en Z.
YZ is het gevraagde lijnstuk.

Toelichting:
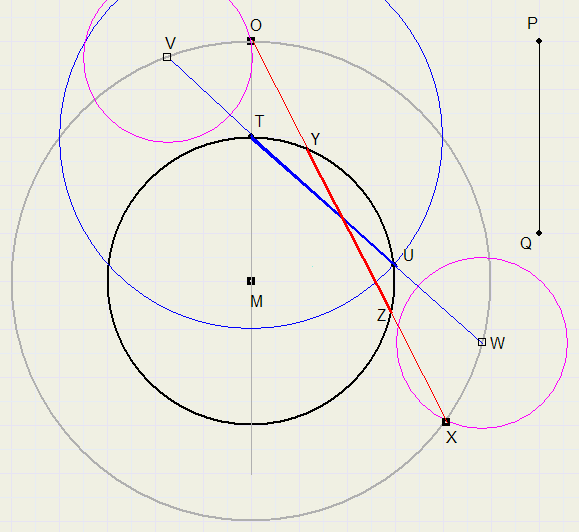
YZ is een rotatie van lijnstuk TU om M.

Oplossing 2 (E.C.Buissant des Amorie)

Stel PQ = 2d.
Bepaal midden van PQ, dus een afstand d.
Trek de lijn door M en O, deze snijdt de cirkel in T.
Construeer de cirkel door punten M en T met straal MT/2.
Cirkel de afstand d om vanuit T, snijpunt met vorige cirkel is U.
Teken cirkel(M,MU).
Construeer de raaklijn door O aan cirkel(M,MU), raakpunt is X.
Deze raaklijn snijdt cirkel(M,r) in punten Y en Z.
YZ is het gevraagde lijnstuk.

Toelichting:
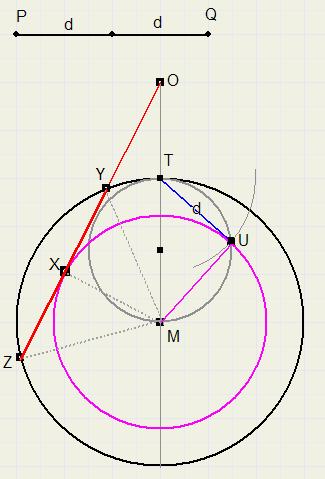
DMUT is congruent met DMXY want
MY = MT = r, MU=MX, LMUT = LMXY = 90^o
zodat :
XY = d, YZ = 2d = PQ

Oplossing 3

(W. de Rijke)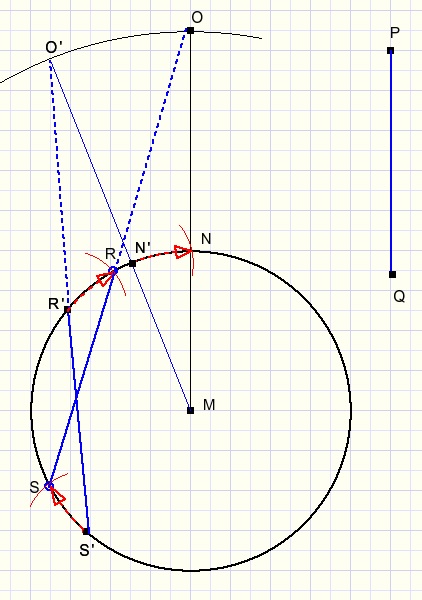

Kies een punt R' op de cirkel.
Cirkel de lengte PQ om vanuit R' en vind S'.
Cirkel nu OM om naar het verlengde van S'R' en vind O'.
De lijnen O'M en OM snijden de cirkel in resp N' en N.
R' en S' verplaatsen over de afstand N'N geeft R en S.

Kijk [hier] voor meetkundige basisconstructies.

Een andere oplossing gevonden?
Laat het weten en uw oplossing wordt toegevoegd.