

 |
Meetkunde puzzel (2) |  |
 |
Oplossing 1 , Oplossing 2
Beschrijving
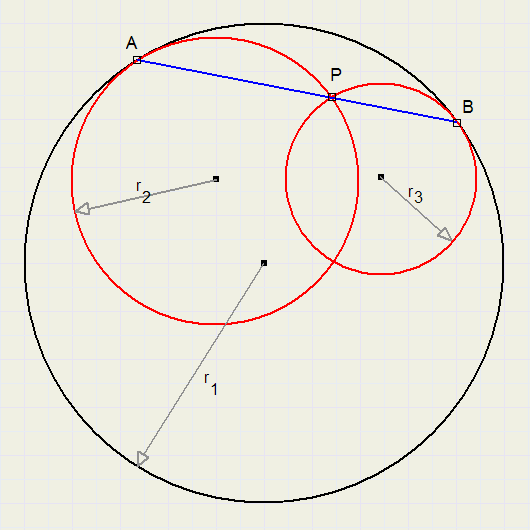
Gegeven is een cirkel met straal r1 met daarbinnen twee inwendig rakende cirkels met straal r2 en r3
Van elke cirkel is ook het middelpunt bekend.
Punten A en B zijn de raakpunten van cirkels 2 en 3 aan cirkel 1.
P is het snijpunt van cirkels 2 en 3.
bewijs nu het volgende:
-
Als P op de lijn AB ligt, dan moet gelden : r1 = r2 + r3
 |
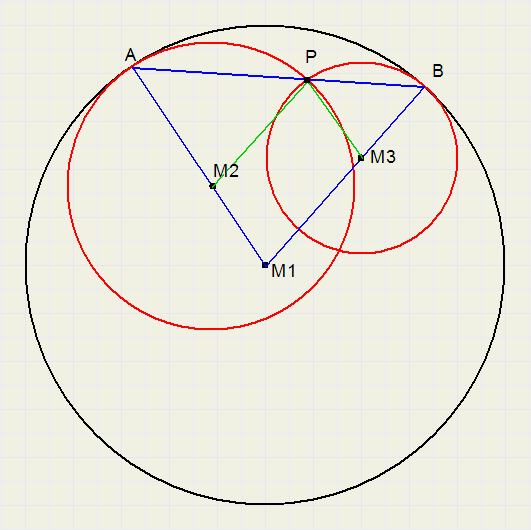
Oplossing van Wim de Rijke
Noem de middelpunten M1, M2 en M3.
Trek AM1 en BM1.
AM1 en AM2 vallen samen, want ze staan loodrecht op dezelfde raaklijn in A.
Evenzo BM1 en BM3. Trek ook PM2 en PM3.
De driehoeken APM2, BPM3 en ABM1 zijn gelijkbenig
en wegens de gemeenschappelijke hoeken bij A en B ook gelijkvormig.
Door de gelijke tophoeken bij M1, M2 en M3 vormt M1M2PM3 een parallellogram.
M1M2 (= r1-r2) is dan gelijk aan PM3 (=r3). Dus r1 = r2+r3.
 |
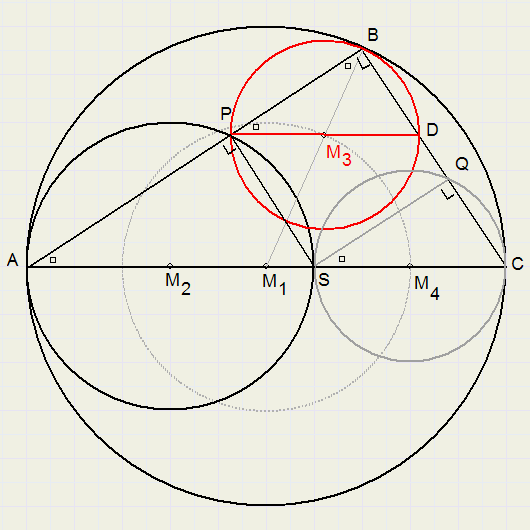
Oplossing van mijzelf
Teken cirkel M4 met middellijn SC op AC.
De hoeken bij P,B en Q zijn 90 graden wegens de stelling van Thales: ze staan op de halve omtrek van de cirkels.
PSQB is een rechthoek. AB en SQ zijn evenwijdig.
Daarom zijn de, met een klein rechthoekje gemerkte, hoeken bij A en S gelijk.
Ook de gemerkte hoeken bij A, P en B zijn gelijk omdat ze bij gelijkbenige driehoeken horen.
(in een driehoek liggen tegenover gelijke zijden gelijke hoeken).
Wegens gelijke hoeken zijn de driehoeken PDB en SCQ gelijkvormig, maar omdat ook PB = SQ zijn ze gelijk (congruent).
Cirkel M3 is daarom gelijk aan cirkel M4
2r1 = 2r2 + 2r3..........{middellijnen}
r1 = r2 + r3
 |


