

| Meetkunde puzzel (8) |  |
Deze puzzel werd onder mijn aandacht gebracht door Omid Motahed, wiskunde docent in Beijing.
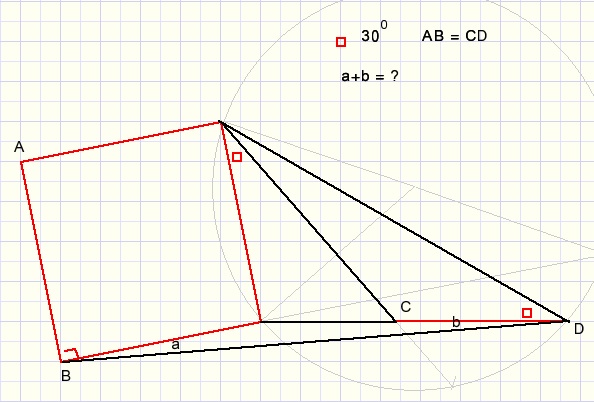
Gegeven is een vierkant en lijnstuk CD = AB.
De met een rood rechthoekje aangegeven hoeken zijn 300
Gevraagd wordt de hoeken a+b te berekenen.
De eerste vraag die opkomt is hoe je deze figuur construeert.
De gelijke hoeken moeten (stelling van Thales) op gelijke cirkelbogen staan.
Het ligt dus voor de hand om een cirkel te construeren door deze hoekpunten met straal AB.
Zet daarvoor op de zijde tegenover AB een gelijkzijdige driehoek.
De tophoek hiervan de het middelpunt van een cirkel met straal AB.
De 300 hoeken staan op cirkelbogen van 600, dus we maken binnen de cirkel
een regelmatige zeshoek, die de cirkel in bogen van 600 verdeelt.
Cirkel lengte AB om vanuit hoekpunten op de cirkel om de hoekpunten van de zeshoek te vinden.
Zie de grijze lijntjes in de tekening hiervoor.
Gevraagd wordt a+b te berekenen.
Bedenkend dat de buitenhoek van een driehoek gelijk is aan de som van de niet aanliggende
binnenhoeken kunnen we het probleem dus ook als volgt stellen:
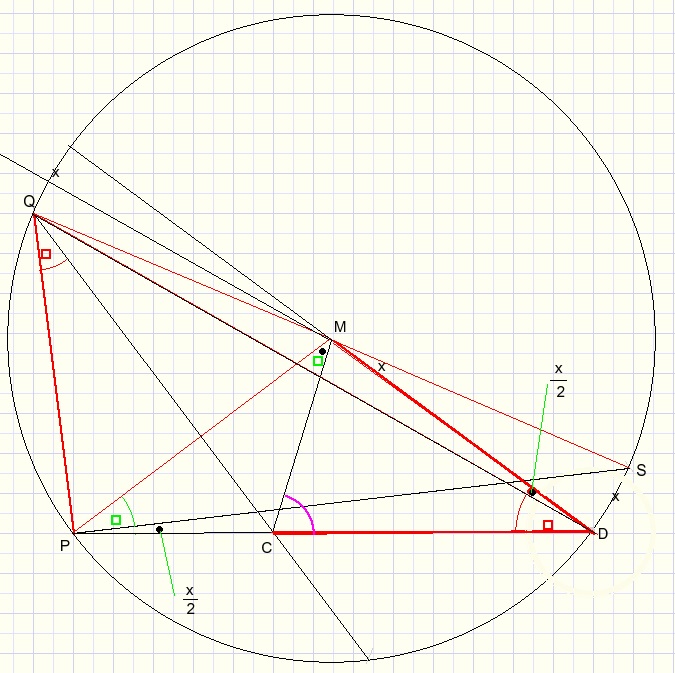
Stel boog DS = x, zodat (a+b) = LSPD = x/2
Het gaat er dus om boog x te berekenen.
Daartoe bekijken we LMCD.
Die is buitenhoek van driehoek PCM maar ook basishoek van gelijkbenige driehoek MCD.
LPQC=300...{gegeven}
LQPS=900...{staat op halve cirkelboog}
zodat
LMPS=90-60=300
2.LMCD + LCDM = 1800
LCDQ=300...{gegeven}
Wegens gelijkbenigheid van driehoek MPC...{C op middelloodlijn van MP} :
kunnen we nu de vergelijking opstellen:
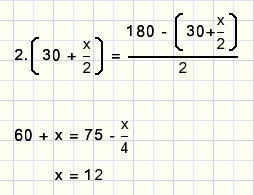
zodat (a+b) = 60

