cursus goniometrie (4)

Inhoud

gonio1Inleiding. sin, cos, tan
gonio2grafieken en trillingen
gonio3sinusregel en cosinusregel
gonio4formules
gonio5vergelijkingen

Inleiding

In dit deel 4 worden de bekendste formules met sin, cos en tan behandeld.
We zetten voor de volledigheid ook eerdere resultaten op een rijtje.
Hieronder staan de grafieken van sin(x), cos(x) en tan(x) bij elkaar

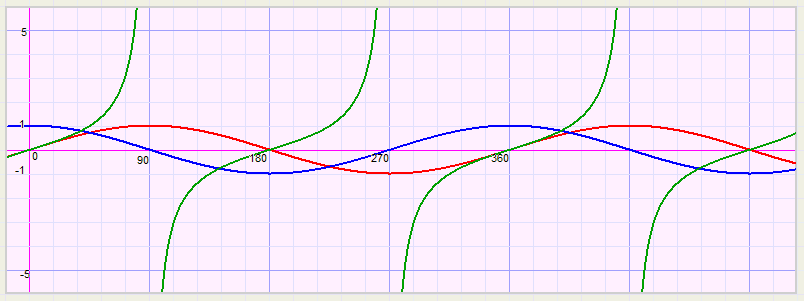
Betrekkingen tussen sin, cos en tan

x is een hoek in graden.
Eerder leidden we af
    sin2(x) + cos2(x) = 1
    tan(x) =
    sin x
    cos x
Binnen een rechthoekige driehoek is te zien dat:
    sin(x) = cos(90 - x)
    cos(x) = sin(90 - x)
    tan(x) = cotg(90 - x)

Periodiciteit

Uit de grafieken lezen we af
    sin(x) = sin(x + k.360)...........................k = ......-3,-2,-1,0,1,2,3,........
    cos(x) = cos(x + k.360)
    tan(x) = tan(x + k.180)

Betrekkingen die volgen uit symmetrie

1. lijnsymmetrie om de Y-as:
    cos(x) = cos(-x)
2. lijnsymmetrie om x = 90
    sin(90 - x) = sin(90 + x)
3. lijnsymmetrie om x = 180
    cos(180 - x) = cos(180 + x)
4. puntsummetrie in (0,0)
    sin(-x) = - sin(x)
    tan(-x) = - tan(x)
5. puntsymmetrie in (90,0)
    cos(90 - x) = - cos(90 + x)
    tan(90 - x) = - tan(90 +x)...............................x ¹ 0
6. puntsymmetrie in (180,0)
    sin(180 - x) = - sin(180 + x)
    tan(180 - x) = - tan(180 + x)

Hoeken die 90 graden verschillen

    sin(x + 90) = cos(x)

bewijs:
sin(x + 90) = cos(90 -(x + 90)) = cos(-x) = cos(x)


    cos(x + 90) = - sin(x)
    tan(x + 90) = - cotg(x)

Hoeken die 180 graden verschillen

    sin(x + 180) = - sin(x)
    cos(x + 180) = - cos(x)
    tan(x + 180) = tan(x)

Voorbeelden
In sin(x), cos(x) of tan(x) kunnen we x omrekenen naar een scherpe hoek
1.
sin(240) = sin(60 + 180) = - sin(60)

2.
cos(290) = cos(180 + 110) = - cos(110) = - cos(90 + 20) = sin(20)



sin(a + b)

    sin(a + b) = sin(a).cos(b) + cos(a).sin(b)

bewijs

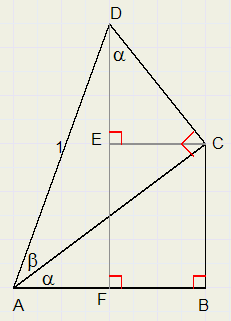
Stel AD = 1.
Dat mag, want het gaat om verhoudingen en niet om absolute afstanden.
In de figuur zien we dan:

    LCDE = a
    CD = sin(b).................zodat
    DE = sin(b).cos(a)
    AC = cos(b)...............zodat
    EF = BC = sin(a).cos(b)
    sin(a + b) = DE + EF = sin(a).cos(b) + cos(a).sin(b)
Veelgebruikte formule voor dubbele hoek:
    sin(2a) = 2sin(a).cos(a)
De sinus van het verschil van twee hoeken:
    sin(a - b) = sin(a).cos(b) - cos(a).sin(b)

bewijs

    sin(a - b) = sin(a +(- b)) = sin(a).cos(- b) + cos(a).sin(- b) = sin(a).cos(b) - cos(a).sin(b)

cos(a + b)

    cos(a + b) = cos(a).cos(b) - sin(a).sin(b)

bewijs

    cos(a + b) = sin((90 - a) - b) =
    sin(90 - a).cos(b) - cos(90 - a).sin(b) =
    cos(a).cos(b) - sin(a).sin(b)
Veelgebruikte formule voor dubbele hoek:
    cos(2a) = cos2(a) - sin2(a)
De cosinus van het verschil van twee hoeken:
    cos(a - b) = cos(a).cos(b) + sin(a).sin(b)

bewijs

    cos(a - b) = cos(a + (- b)) =
    cos(a).cos(- b) - sin(a).sin(- b) =
    cos(a).cos(b) + sin(a).sin(b)

tan(a + b)




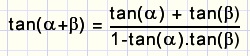
bewijs




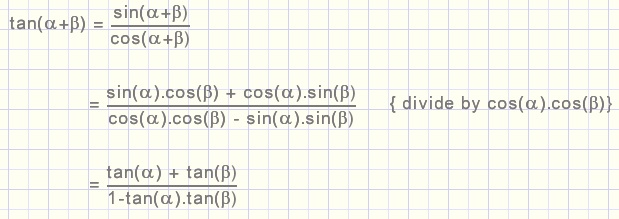
Veelgebruikte formule voor dubbele hoek:



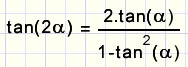
Formule voor de tangens van het verschil van twee hoeken



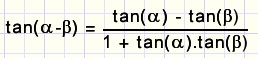
het bewijs laat ik aan de lezer over


sin(a) + sin(b)




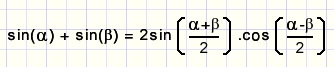
bewijs:
Uit de formules voor de sinus van som en verschil van twee hoeken volgt:

    sin (p + q) +  sin (p − q) = 2 ·  sin p ·  cos p

stel nu

    p + q = a
    p − q = b ......dan is.....
    2 p = a + b ....zodat....



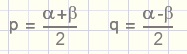
Formule voor het verschil van twee sinussen



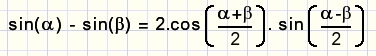
Het bewijs laat ik aan de lezer over


cos(a) + cos(b)




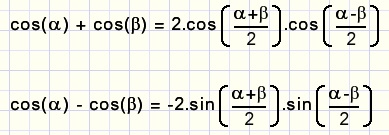
het bewijs is voor de lezer


De laatste vier formules maken het mogelijk de som (verschil) van twee sinus- of cosinus functies om te zetten
in een product (en omgekeerd).

Voorbeeld
1.
sin(40) + sin(20) = 2.sin(30).cos(10) = cos(10)
2.
sin(50).sin(60) = 0,5*2*sin(50).cos(20) = 0,5*(sin(70)+sin(30))



Met wat algebraïsch gegoochel zijn allerlei formules op te stellen.

Opgaven

1.
bewijs dat in een driehoek met hoeken a,b,c geldt:



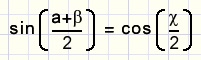
2.
In een driehoek ligt zijde a tegenover hoek a.
De hoekpunten van de driehoek liggen op een cirkel met straal R.
bewijs dat



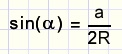
(denk aan de stelling van Thales)


3.
bewijs, dat
a.
sin (3 a) = 3 ·  sin a − 4 ( sin a) 3
b.



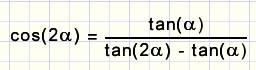
4.
bewijs dat
cos (2 a) = 1 − 2 ( sin a) 2

5.
Gegeven is : a+b+c = 180.
bewijs dat:.... tan(a) + tan(b) + tan(c) = tan(a).tan(b).tan(c)

6.
bewijs, dat



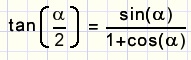
7.
bewijs dat
sin (2 a) +  tan (2 a) = 2 ·  tan (2 a) ( cos a) 2

8.
bewijs dat



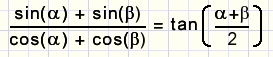
9.
schrijf als product:
a. sin (3 a) +  sin a
b. sin a −  cos a
c. sin a +  sin (3 a) +  sin (5 a) +  sin (7 a)

10.
schrijf als som of verschil:
a. 2 ·  sin (2 a) ·  cos a
b. sin (2 a) ·  sin a
c. sin (3 a) ·  cos (4 a)


succes!



Antwoorden
1.
stel (a + b)/2 = p, dan c/2 = 90 - p
sin(p) = cos(90 - p)

2.
Stel hoek a staat op cirkelboog AB
Teken middellijn AC, C op cirkel.
Teken BC .
LBCA = a LCBA = 90 graden (Thales)
enz.

Vooraf:
Bij de volgende opgaven moet een gelijkheid worden bewezen.
Of die klopt kan eenvoudig worden nagegaan door de formules links en rechts
van het = teken te plotten. De grafieken moeten samenvallen.
Gebruik Graphics Explorer met letter x voor de hoek.
Selecteer graden, vervangen en stel de x as in op zo'n 10..30 graden per schaaldeel.

3.
sin (3 a) =
sin (2 a + a) =
sin a ·  cos (2 a) +  cos a ·  sin (2 a)
enz.

4.
tan (2 a) schrijven als tan a
dan



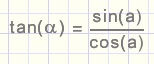
en vereenvoudigen.

5.
tan c schrijven als − tan (a + b) dat weer schrijven als tan a en tan b en uitwerken.

6.



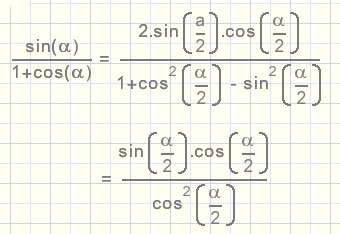
etc.

7.
NB: sin (2 a) =  tan (2 a) ·  cos (2 a)
sin (2 a) +  tan (2 a) = tan (2 a) ·  cos (2 a) +  tan (2 a) =
tan (2 a) · ( cos (2 a) + 1) =
tan (2 a) · (( cos a) 2 − ( sin a) 2 + 1) =
2 ·  tan (2 a) ( cos a) 2

8.



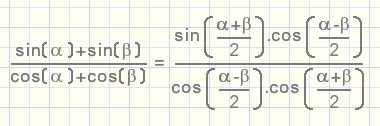
etc.

9.
a.
sin (3 a) +  sin a = 2 ·  sin (2 a) ·  cos a
b.
sin a −  cos a =
sin a −  sin (90 − a) =
sin a +  sin (a − 90) =
2 ·  sin (a − 45) ·  cos 45
c.
sin a +  sin (3 a) +  sin (5 a) +  sin (7 a) =
2 ·  sin (4 a) ·  cos (3 a) + 2 ·  sin (4 a) ·  cos a =
2 ·  sin (4 a) ( cos (3 a) +  cos a) =
2 ·  sin (4 a) (2 ·  cos (2 a) ·  cos a) =
4 ·  sin (4 a) ·  cos (2 a) ·  cos a

10.
a.
sin (3 a) +  sin a
b.



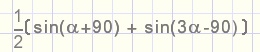
c.