

 |
cursus goniometrie (3) |  |
 |
Inhoud
| gonio1 | Inleiding. sin, cos, tan | |
| gonio2 | grafieken en trillingen | |
| gonio3 | sinusregel en cosinusregel | |
| gonio4 | formules | |
| gonio5 | vergelijkingen |
Inleiding
Hiervoor rekenden we met rechthoekige driehoeken.Maar de goniometrie kan ook worden toegepast op willekeurige driehoeken.
Wel zijn dan twee extra formules nodig.
Die behandel ik hier in deel 3.
de sinusregel
Bekijk de figuur hieronder: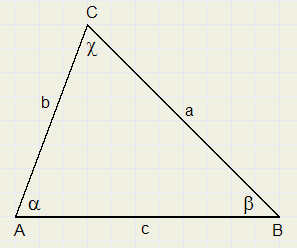
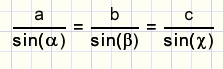
bewijs
-
h = b.sin(a)...................en ook
h = a.sin(b)
zodat.........
a.sin(b) = b.sin(a)
dus
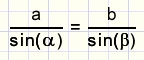
enzovoorts. (we hadden ook een hoogtelijn uit een ander hoekpunt kunnen trekken)
-
In een willekeurige driehoek geldt:
Een zijde gedeeld door de sinus van de overstaande hoek levert steeds een zelfde waarde op.
Voorbeeld (1)
Twee landmeters, A en B, meten de hoek tussen een toren T en de ander.
Zie het plaatje hieronder.
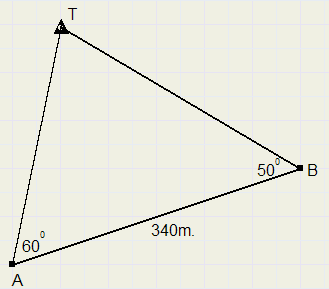
De afstand tussen de landmeters is 340 meter.
Bereken de afstanden AT en BT.
De hoek bij T is : 180 - 50 - 60 = 70 graden.
Nu weten we in driehoek ABT een hoek en ook de lengte van de zijde ertegenover.
Daarom kunnen we van de sinusregel gebruik maken.

We merken op, dat de sinusregel niet werkt als alleen de zijden van een driehoek bekend zijn.
Daarvoor is de volgende regel nodig.
de cosinusregel
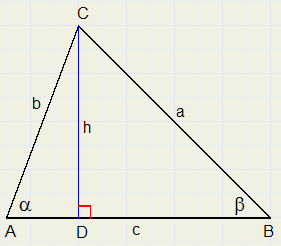
Die luidt: (zie plaatje bovenaan deze pagina)-
a 2 = b 2 + c 2 − 2 b c · cos a
bewijs
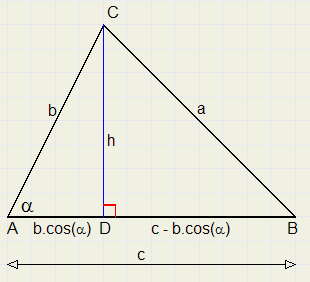
BD = c - b.cos(a)
Pythagoras toepassen in driehoeken ADC en DBC levert
-
h2 = b2 - (b.cos(a))2
h2 = a2 - (c - b.cos(a))2
zodat
a2 - (c - b.cos(a))2 = b2 - (b.cos(a))2......haakjes wegwerken.....
a2 - c2 + 2bc.cos(a) - b2.cos2(a) = b2 - b2.cos2(a)
a2 = b2 + c2 - 2bc.cos(a)
Als LB = b en LC = c dan geldt:
-
b2 = a2 + c2 - 2ac.cos(b)
en ook
c2 = a2 + b2 - 2ab.cos(c)
Voorbeeld (2)
We berekenen BC in driehoek ABC, zie plaatje hieronder
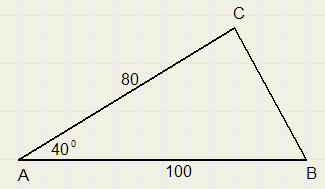
Aan de sinusregel hebben we hier niets, omdat er geen hoek met tegenoverliggende zijde bekend is.
cosinusregel:
-
BC2 = 802 + 1002 - 2*80*100*cos(40) = 4143
BC = 64,37
Voorbeeld (3)
We berekenen de hoeken van een driehoek als alle zijden bekend zijn.
Van driehoek PQR is.....PQ = 5, QR = 8, RP = 7.
QR is de zijde tegenover LP, zodat (cosinusregel)
-
82 = 72 + 52 - 2*7*5*cos(LP)
cos(LP) = 0,142285
LP = bgcos(0,142285) = 81,8 graden
Nu is er een zijde met tegenoverliggende hoek bekend, zodat de overige hoeken
eenvoudiger met de sinusregel berekend kunnen worden:
-
sin(LQ) = (7.sin(81,8) / 8 = 0,866
LQ = bgsin(0,866) = 60 graden
Vectoren
Even een aanloopje naar andere toepassingen van de goniometrie.Sommige grootheden, zoals gewichten of secondes, kunnen we optellen.
Maar dat kan niet bij grootheden die behalve een grootte ook een richting hebben.
Dat laatste is het geval bij
- afstanden
- snelheden
- krachten
- trillingen die niet in fase zijn
Dit soort grootheden heten "vectoren".
Met behulp van de goniometrie kunnen we wel vectoren optellen.
Het aardige is, dat voor alle bovenstaande gevallen het rekenwerk gelijk is.
Optellen van krachten
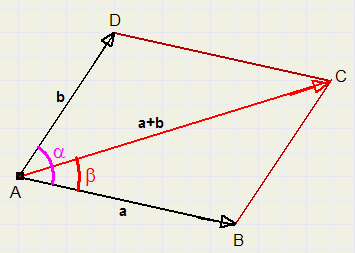
Dat zijn vectoren, wat we aangeven door de letters dik te drukken.
De lengtes van AB en AD geven de grootte van die krachten aan.
Die grootte, ongeacht de richting, heet de absolute waarde van een vector en die wordt aangegeven
door vertikale streepjes te zetten.
Zo is |a| de absolute waarde van vector a, dat is hetzelfde als de lengte van AB.
AC is de optelling van a en b.
AC is ontstaan door AD evenwijdig te verschuiven totdat punt A op punt B ligt, dus punt D ligt dan op C.
Zo ontstaat een zogenaamd parallellogram van krachten ABCD.
De vraag is nu wat (gegeven AB, AD en hoek a) de lengte is van AC = a + b en de grootte van hoek b
De cosinusregel biedt de oplossing.
LCDA = 180 - a, laten we die even c noemen.
Bekijk nu driehoek ACD, waarin CD = AB (eigenschap parallellogram):
-
AC2 = AB2 + AD2 - 2*AB*AD*cos(c)
en omdat geldt..............cos(180-a) = -cos(a):
AC2 = AB2 + AD2 + 2*AB*AD*cos(a) ............anders geschreven...........
|a+b|2 = |a2| + |b2| + 2.|a|.|b|.cos(a)
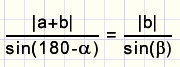
en omdat sin(180-a) = sin(a)................
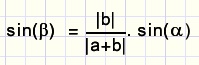
De krachten AB en AD mogen dus worden vervangen door kracht AC.
Als AB en AD bijvoorbeeld krachten zijn die worden uitgeoefend op een tentstok A,
dan kan evenwicht worden bereikt door in A een derde kracht (scheerlijn) even groot als AC
maar met tegengestelde richting aan te brengen.
Merk op:
Uitgaande van AC, kan AC worden vervangen door de krachten AB en AD.
Dat heet : ontbinden van krachten
Voorbeeld (4)
Boven een straat is een reclamebord opgehangen aan kabels, die aan de gevels van huizen zijn bevestigd.
Het bord weegt 25kg.
Bereken de kracht in elke kabel.
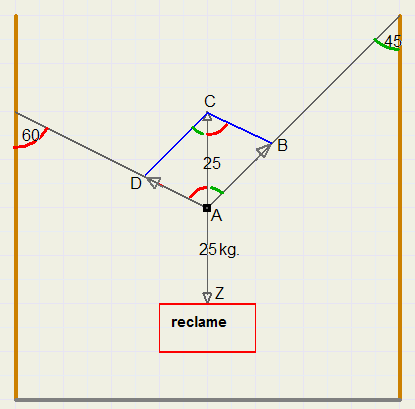
De kracht omlaag (AZ) van 25kg. moet worden opgeheven door een evengrote kracht omhoog (AC).
Vanuit punt C zijn lijnen getrokken evenwijdig aan de kabels, zodat parallellogram ABCD ontstaat,
waarin kracht AC wordt ontbonden in krachten AB en AD, die in de kabels werken (AC = AB + AD).
In de figuur hebben evengrote hoeken eenzelfde kleur gekregen.
We zien, dat LABC = 180 - 60 - 45 = 75 graden.
Sinusregel:
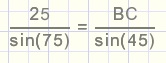
BC = AD = 18,3kg.....de kracht in de linker kabel.
net zo:
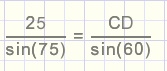
AB = CD = 22,4kg. .....de kracht in de rechter kabel
Interessant is nog om de krachten in de kabels te ontbinden in een horizontale- en een vertikale kracht.
De horizontale kracht kan namelijk zorgen voor het uit de muur trekken van de bout waaraan de kabel vastzit.
In onderstaande figuur wordt de kracht F ontbonden.
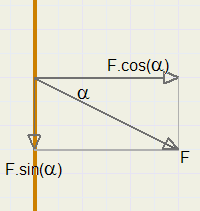
Voor de linker muur geldt Fhor = 18,3cos(30) = 15,85kg.
Voorbeeld (5)
Een pont vaart een rivier over van A naar B, zie plaatje hieronder.
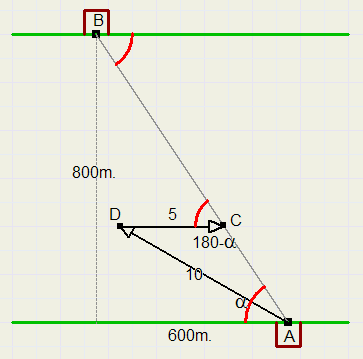
De rivier stroomt met een snelheid van 5km per uur.( = vector DC)
De pont vaart met een snelheid van 10km. per uur over het water.(= vector AD)
De echte beweging (AC) van de pont t.o.v. de grond is de (vector) optelling van deze snelheden.
C moet op de lijn AB liggen.
Vraag: bereken de richting (hoek met de oever) waaronder de pont moet varen om in B aan te komen.
In de figuur hierboven hebben gelijke hoeken eenzelfde kleur gekregen.
a = bgtan(800/600) = 53 graden.
Omdat sin(a) = sin(180-a) geldt: (sinusregel in driehoek ACD)
(stel LCAD = b)
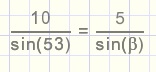
sin b = 0.4
b = 23.5 graden
De pont moet dus varen onder een hoek van 53 - 23,5 = 29,5 graden met de oever.
Voorbeeld (6)
Een hijsinrichting bestaat uit een boom (ST, scharnierpunt S en top T),
die een hoek van 60 graden maakt met de grond. De lengte van de boom is 40m.
De boom wordt omhooggehouden door een kabel AT, waarbij AS = 25m.
(verwaarloos het gewicht van de boom)
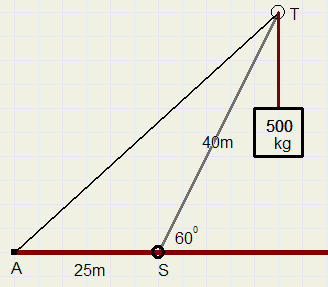
Als de kraan een gewicht tilt van 500kg. , bereken dan de kracht in de kabel.
De kracht van de last die wordt opgetild is de (vector) optelling van de krachten die in boom ST en kabel AT optreden.
Die krachten hebben een tegengestelde richting want
- Boom ST wordt ingedrukt
- kabel AT wordt uitgerekt
We ontbinden dus de kracht van 500kg. in tegengestelde krachten in richtingen AT en ST.
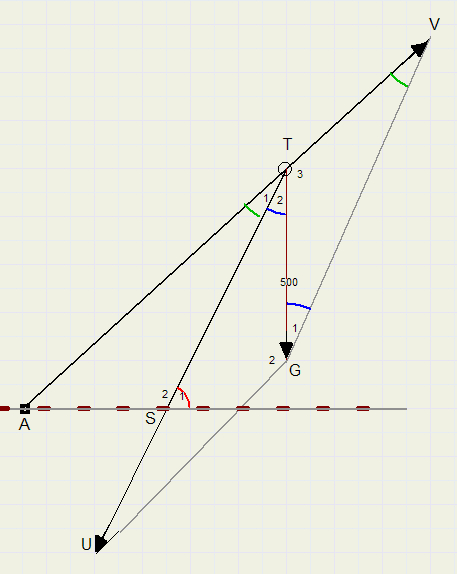
In de figuur hierboven is (vector) TG = TU + TV.
UGVT is een parallellogram.
Te berekenen is dus de lengte van TV.
Toepassen van de sinusregel in driehoek GVT ligt voor de hand.
Daarvoor moet bijvoorbeeld eerst LV = LT1 worden berekend.
De sinusregel in driehoek AST kan LT1 leveren als tenminste AT bekend is.
Die is met de cosinusregel te berekenen.
LS2= 120 graden, zodat (cosinusregel in driehoek AST)
-
AT2 = 252 + 402 - 2*25*40*cos(120) = 3225.
AT = 57
sinusregel in driehoek AST
-
sin(LT1) = (25/57)*sin(120) = 0,38
LT1 = 22 graden
sinusregel in driehoek GVT (LG1 = LT2 = 30 graden)
-
TV = 500*sin(30)/sin(22) = 667 kg.
Opgaven
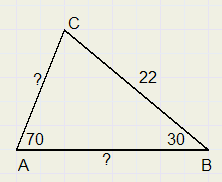
1.
2.
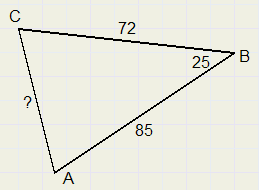
3.
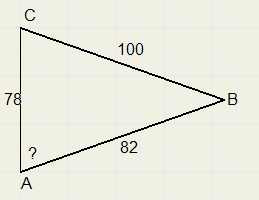
4.
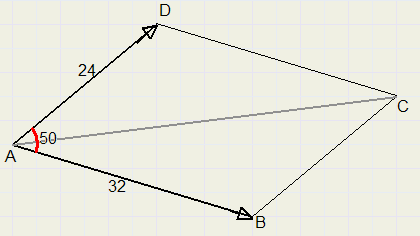
Bereken AC
5.
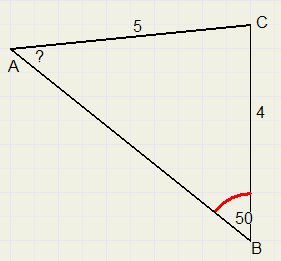
6.
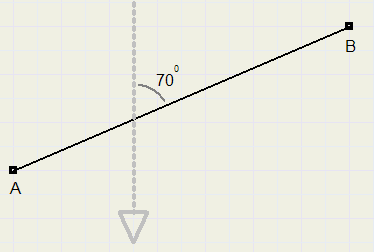
De straalstroom (luchtstroom op grote hoogte) bedraagt 150 km/uur.
De snelheid van het vliegtuig is 800km/uur.
Zie plaatje voor de richting van de straalstroom.
Welke richting moet het vliegtuig aanhouden om rechtstreeks naar B te vliegen?
Hoe lang duurt de vlucht?
7.
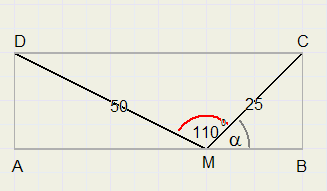
Bereken hoek a
8.
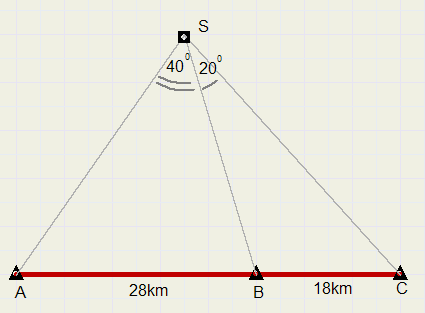
Zie plaatje.
Bereken de afstanden AS,BS en CS.
9.
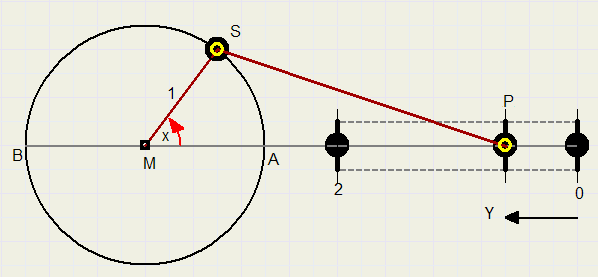
P en S zijn scharnierende koppelingen.
PS heeft lengte L.
S draait rond op het wiel met middelpunt M.
P beweegt heen en weer.
Als S in punt A staat, bereikt P de meest rechtse stand. (y = 0)
Bij S in punt B wordt de meest linkse stand bereikt (y = 2).
x is de hoek waarover S is gedraaid.
Bereken de functie y = f(x)
Is de grootte van L van invloed?
10.
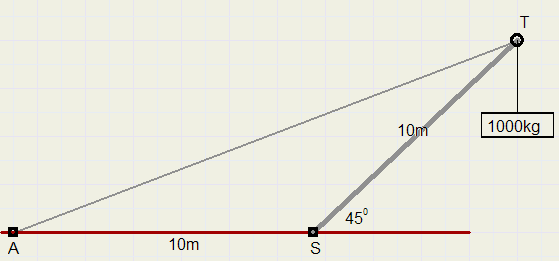
Een kraan bestaat uit een hefboom ST, die door een kabel AT omhoog wordt gehouden.
Bereken de kracht in de kabel als de kraan een gewicht heft van 1000kg.
 succes!
succes!Antwoorden
1.
AB=23,05
AC=11,7
2.
AC=36,27
3.
LA = 77,3 graden
4.
AC = 50,88
5.
La = 37,79 graden
6.
afwijkende hoek 10,15 graden noordelijk.
tijd = 3 uur, 16 min.
7.
a = 48,14 graden
8.
AS = 41,12
BS = 40,73
CS = 49,68
9.
y = L + 1 - cos(x) - W(L2 - sin2(x) ).........................W is wortel
10.
1848 kg

