

 |
cursus goniometrie (2) |  |
 |
Inhoud
| gonio1 | Inleiding. sin, cos, tan | |
| gonio2 | grafieken en trillingen | |
| gonio3 | sinusregel en cosinusregel | |
| gonio4 | formules | |
| gonio5 | vergelijkingen |
de grafiek van de functie y = sin(x)
Hierin is x de hoek in graden en y is de functiewaarde.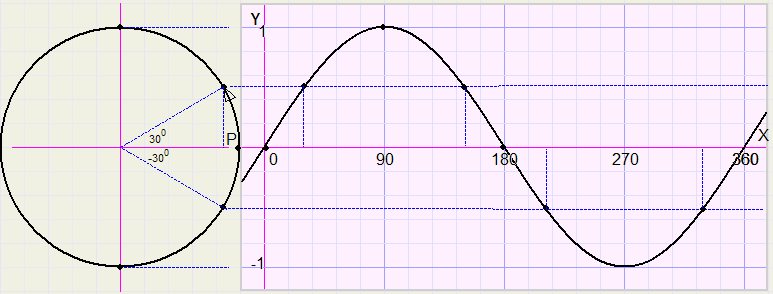
gelijk is aan sin(x), waarbij x de hoek is waarover P is gedraaid.
Bij x = 90 graden wordt de grootste waarde (1) bereikt en bij x = 270 de kleinste waarde (-1).
Nulpunten treden op voor x = 0 en x = 180 graden.
Verder zien we verschillende symmetrieŽn
-
- puntsymmetrie ten opzichte van de oorsprong (0,0)
- symmetrie om de verticale lijnen x = 90 en x = 270
sin(x) is negatief in kwadranten 3 en 4 (180 < x < 360 graden).
Uit de symmetrie volgt nog dat
-
1............sin(x) = sin(180 - x)
2............sin(90 - x) = sin(90 + x)
Na 360 graden herhaalt de grafiek zichzelf : de periode is 360 graden, zodat
-
sin(x) = sin(x + k.360)..............waarbij k = 0,1,2,3,4,.........
-
sin(-x) = - sin(x) ......................het gevolg van de puntsymmetrie
Linkom draaien levert een positieve-, rechtsom een negatieve hoek op.
Trillingen
Trillingen hebben (vaak) een sinusvorm: trillende veren, de slinger van een uurwerk, luidsprekers.y is dan de uitslag of de luchtdruk.
De netspanning is ook sinusvormig omdat die het gevolg is van draaiende spoelen in een magnetisch veld.
Amplitude
Dit is de maximale functiewaarde - de evenwichtsstand.De sinusfunctie hierboven heeft een amplitude van 1 en een evenwichtsstand van 0.
Als de amplitude A is en de evenwichtsstand B, dan wordt de functie
-
y = A.sin(x) + B
Periode en frequentie
De functie y = sin(x) heeft een periode van 360 graden.Vervangen we x door x/2 , dan verdubbelt de periode.
Vervangen we x door 2x, dan halveert de periode, immers: 2x heeft nu een periode van 360, dus x van 180.
Bij een periode p is de oorspronkelijke periode vermenigvuldigd met p/360,
zodat x moet worden vermenigvuldigd met het omgekeerde:
-
y = sin(360/p . x) ................heeft een periode van p graden, immers....x = p levert op ....sin(360)
De trilling
-
U = 5sin(t)
heeft een amplitude van 5 en een periode van 360 seconde.
Voor een periode van T wordt de functie
-
U = 5sin(360 * t / T)
-
f = 1 / T
-
U = 5sin(360*f*t)
- U : de momentele spanning in Volt
- 50: de frequentie (trillingen per seconde)
Opmerking: 220 is de effectieve waarde van de netspanning, niet de amplitude
Fase
als in y = sin(x) ......x wordt vervangen door x-1 dan schuift de grafiek 1 graad naar rechts.Zo'n verschuiving heet bij trillingen een faseverschuiving.
Een algemene formule van een trilling met
- amplitude A
- evenwichtsstand B
- frequentie f
- faseverschuiving P
luidt
-
U = A.sin(360.f.t - P) + B....of bij periode T....
U = Asin(360.t/T - P) + B
P is de verschuiving ten opzichte van een hele periode.
Als er een verschuiving v plaatsvindt (naar rechts) op de schaal van t, dan moet t worden vervangen door (t - v)
en de verschuiving t.o.v. een hele fase wordt dan ......360.f.v
......immers.... sin(360.f(t - v)) = sin(360.f.t - 360.f.v)
Voorbeeld (1)
We bedenken de functie van de trilling hieronder:
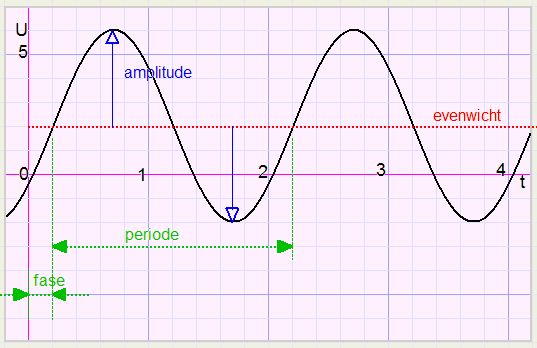
we zien:
- een evenwichtsstand van 2
- een amplitude van 4
- een periode van 2
- een verschuiving van 0,2 op de schaal van t
Uitgaande van..............U = 4sin(....t...) + 2 ........met een periode van 360.............is dus
t vermenigvuldigd met..............360/2 = 180 om een periode van 2 te krijgen.
zodat
U = 4sin(180t - ...) + 2
De faseverschuiving is 0,2 (naar rechts, dus later in de tijd) .....zodat t moet worden vervangen door (t - 0,2)
en de functie wordt:
-
U = 4sin(180(t - 0,2)) + 2...........of
U = 4sin(180t - 36) + 2
Voorbeeld (2)
Een reuzenrad draait (tegen de klok) rond in 50 seconden.
Het rad heeft een diameter van 24 meter. Zie het plaatje hieronder.
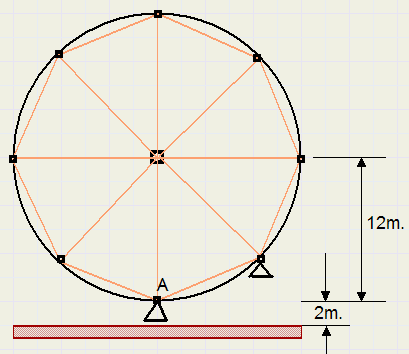
Passagiers stappen in bij punt A.
Bereken de hoogte van A boven de grond t seconden nadat het rad is gaan draaien.
De evenwichtsstand is 12 + 2 = 14 meter boven de grond.
de amplitude is 12 meter.
Daarmee wordt de functie H = 12sin(...t...) + 14
Maar de priode is geen 360, maar 50 seconden, zodat (t vermenigvuldigen met 360/50 = 7,2)........
-
H = 12sin(7,2t........) + 14
Maar de passagiers stappen 1/4 * 50 = 12,5 seconden in vůůr de evenwichtsstand (of 1/4 deel van een periode)
t moet dus worden vervangen door (t - 12,5)...........zodat
-
H = 12sin(7,2(t-12,5)) + 14 ...............of
H = 12sin(7,2t - 90)
de grafiek van de functie y = cos(x)
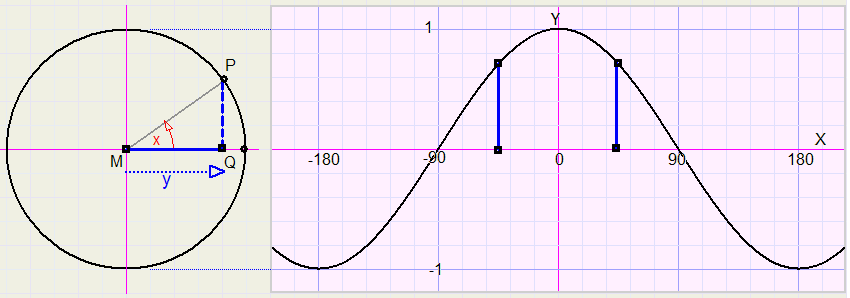
Bij een straal van 1 van de cirkel is de cosinus van hoek x de projectie van MP op de horizontale as,
dus de afstand MQ.
In de grafiek zien we de volgende symmetrieŽn
-
- om de y-as....................dus...........cos(-x) = cos(x)
- om de lijn y = 180..........dus...........cos(180-x) = cos(180 + x)
- om punt (90 , 0).............dus...........cos(90 - x) = - cos(90 + x)
-
cos(x) positief is in de kwadranten 1 en 4................(-90 < x < 90)
cos(x) negatief is in kwadranten 2 en 3...................(90 < x < 270)
-
cos(x) = cos(x + k.360).............waarbij k= 0,1,2,3,........
ontstaat door sin(x) 90 graden naar links te schuiven, zodat
-
cos(x) = sin(x + 90)
Wegens lijnsymmetrie geldt........sin(90 - x) = sin(90 + x), zodat ook...........cos(x) = sin(90 - x)
Cos(x) heeft als grootste waarde 1 en als kleinste waarde -1.
Nulpunten treden op bij 90 + k.180 graden (k = .....-2, -1, 0, 1, 2,......)
de grafiek van de functie y = tan(x)
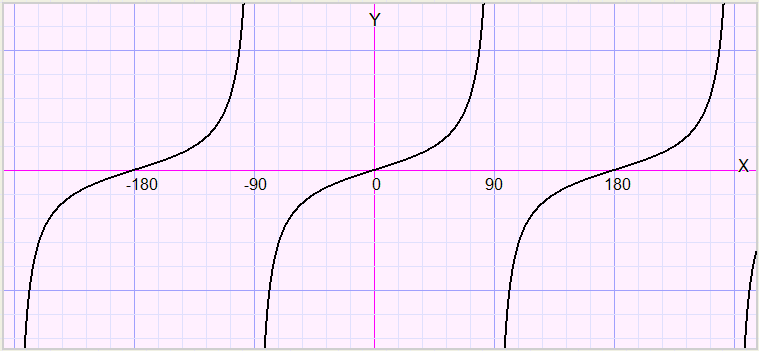
We zien
-
- puntsymmetrie t.o.v.de oorsprong (0,0).................dus tan(-x) = - tan(x)
- asymptoten voor x = 90 en x = -90..................tan(x) wordt oneindig groot (klein) voor x = 90 graden
1..... tan(x) = sin(x) / cos(x)............de asymptoten treden op als cos(x) = 0
2......de tangens is hetzelfde als het hellingsgetal a in lineaire functie y = ax + b
Opgaven (10 punten per opgave)
1.y = 8sin(x) - 5
Bereken de minimale en de maximale waarde van y
2.
y = sin(3x)
wat is de periode (in graden) van y?
3.
bekijk de twee functies
-
y = sin(3x)
y = sin(3x - 30)
b. Hoeveel bedraagt de verschuiving op de x-as?
4.
y = A.sin(x) + B
Op x = 0 geldt: y = 4. Op x = 30 graden geldt y = 1.
bereken A en B
5.
y = sin(p.x)
Op x = 90 graden geldt: y = 0,5
Bereken p
6.
y = 9sin(5x)
Wat is de periode van y?
7.
Een trilling (bijvoorbeeld een bol aan een trekveer) heeft een periode van 1 seconde een amplitude van 5.
Op t= 0 is de positie van de bol 0
Welke functie beschrijft de trilling?
8.
y = A.sin(px) + B heeft een maximale waarde van 10 en een minimale waarde van 2.
Op x = 30 (graden) wordt de maximale waarde bereikt.
bereken A,B en p
9.
Een fietswiel heeft een diameter van 88cm.
Onderop het wiel, waar het de grond raakt, wordt een punt getekend.
Welke functie H = .....sin(.....a....) geeft de hoogte H van het punt boven de grond als de fiets a meter heeft afgelegd?
10.
y = sin(x) + sin(x+60)
Schrijf bovenstaande functie als y = ...sin(....x...) , dus ťťn sinusfunctie en geen optelling van twee.
(denk aan een cirkel met ronddraaiende pijlen)
succes!
Antwoorden
1.
-13 , 3
2.
120 graden
3.
a. 30 graden
b. 10 graden
4.
A= -6
B= 4
5.
p = 1/3
6.
72 graden
7.
y = 5sin(360t)
8.
p = 3
A = 4
B = 6
9.
H = 44(1 - cos(1,3a))
10.
y= W(3) sin(x + 30)......................{W is wortel}


