

 |
cursus goniometrie (1) |  |
 |
Inhoud
| gonio1 | Inleiding. sin, cos, tan | |
| gonio2 | grafieken en trillingen | |
| gonio3 | sinusregel en cosinusregel | |
| gonio4 | formules | |
| gonio5 | vergelijkingen |
Inleiding
Goniometrie heet ook wel driehoeksmeting.Hoewel het alleen lijkt te gaan om meetkunde, is de toepassing van de goniometrie veel breder.
Buiten de landmeetkunde wordt goniometrie ook toegepast bij mechanische- en elektromagnetische trillingen,
dus radio, TV, mobiele telefonie en de elektriciteitsvoorziening.
Daarnaast is er ook ruime toepassing bij sterkteberekeningen.
Goniometrie is gebaseerd op de eigenschappen van gelijkvormige driehoeken.
Twee driehoeken heten gelijkvormig als de één een vergroting is van de ander.
Bij die vergroting blijven de hoeken gelijk.
Twee driehoeken zijn gelijkvormig als ze gelijke hoeken hebben.
Om aan te tonen dat twee driehoeken gelijkvormig zijn is het voldoende om aan te bewijzen dat ze twee
gelijke hoeken hebben: de derde is dan vanzelf ook gelijk.
Er wordt uitgegaan van rechthoekige driehoeken.
Twee rechthoekige driehoeken zijn gelijkvormig als ze één scherpe hoek gelijk hebben.
Dit is de hoofdeigenschap waar de goniometrie op rust:
-
gelijkvormige driehoeken hebben een vaste verhouding van hun overeenkomstige zijden
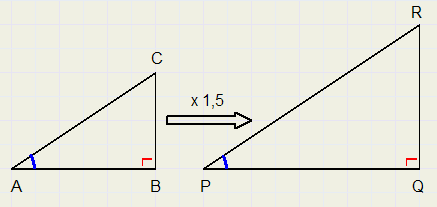
De hoeken bij A en P zijn gelijk en ook die bij C en R.
Overeenkomstige zijden zijn:
- AB en PQ
- BC en QR
- AC en PR
Zodoende is bijvoorbeeld

Bij een bepaalde scherpe hoek (LA) hoort dus een bepaalde verhouding tussen de zijden.
En omgekeerd:
als in een rechthoekige driehoek de verhouding bekend is van twee zijden, dan staan de hoeken vast.
We merken op, dat de verhouding van twee zijden een dimensieloos getal is, het is een factor.
Omdat er drie zijden zijn, zijn er zes verhoudingen van zijden op te stellen.
Bekijk driehoek ABC hieronder met rechthoekszijden a en b en schuine zijde c.
LB = a graden
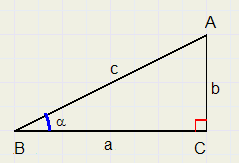

Minder bekende en weinig gebruikte verhoudingen zijn

In een rechthoekige driehoek is dus
-
de sinus van een hoek:........overstaande rechthoekszijde gedeeld door schuine zijde
de cosinus van een hoek:....aanliggende rechthoekszijde gedeeld door schuine zijde
de tangens van een hoek:....overstaande- gedeeld door aanliggende rechthoekszijde
Zo'n berekening zelf maken ligt nog niet in ons bereik, maar hier komt de rekenmachine te hulp.
Die heeft knopjes sin, cos en tan om deze functies te vervullen.
Met bovenstaande kennis zijn al dit soort berekeningen te maken:
Voorbeeld
Zie figuur hieronder.
Gegeven is de rechthoekige driehoek ABC met AC = 12 en LB = 36 graden.
Bereken de andere zijden.
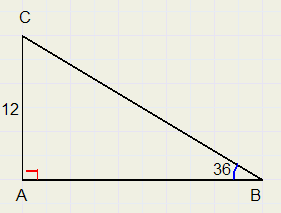
Doordat één scherpe hoek van de rechthoekige driehoek bekend is, liggen de verhoudingen tussen de zijden vast.
Voor de berekening van BC is het handig om van de sinus van LB uit te gaan.
sin LB = sin 36 = 0,588...(volgens rekenmachine) .........zodat
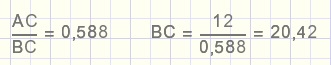
Voor de berekening van AB kunnen we uitgaan van de tangens van LB
tan LB = tan 36 = 0,727..(volgens rekenmachine) ......zodat
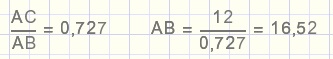
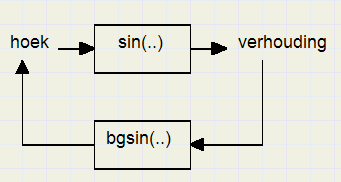
Omgekeerde sinus, cosinus en tangens
Van een gegeven hoek kan de sinus, cosinus of tangens berekend worden.Uit een gegeven sinus, cosinus of tangens kan de hoek worden berekend.
Hieronder staat een tabel met de goniometrische functies, hun omgekeerde en het opschrift van het knopje op de rekenmachine
| functie | omgekeerde | knopje rekenmachine | |
| sin | bgsin | sin-1 | |
| cos | bgcos | cos-1 | |
| tan | bgtan | tan-1 |
Voorbeeld
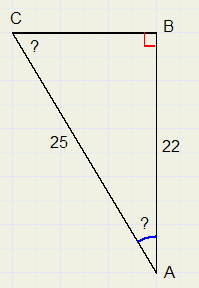
Bereken LA en LC als AB = 22 en AC = 25.
Het is handig om uit te gaan van de cosinus van LA:
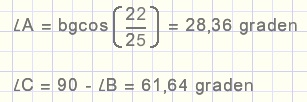
Als sin(a) = x dan geldt:
-
sin(bgsin(x)) = x..........en ook
bgsin(sin(a)) = a
Voorbeeld
Een boer heeft een cirkelvormig stuk land met een straal van 50 meter.
Op de rand plaatst hij twee palen met een onderlinge afstand van 30 meter.
zie figuur hierna.
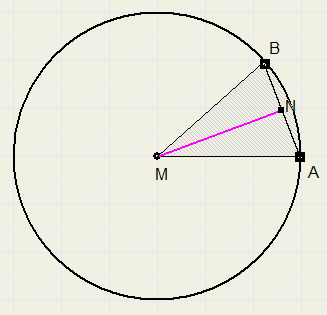
Bereken de oppervlakte van cirkelsegment BMA.
Door een hulplijn te trekken door midden M van de cirkel en midden N van AB, ontstaat rechthoekige driehoek MAN
Wegens symmetrie is AN = 15.
MA = 50.
Dus LNMA = bgsin(15/50) = 17,5 graden................LBMA = 35 graden.
De oppervlakte van segment BMA = (35/360) p502 = 762
Verbanden tussen sin, cos en tan
1.In een rechthoekige driehoek met rechthoekszijden a en b en schuine zijde c geldt (Pythagoras)

2.
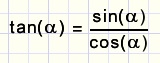
de lezer mag dit zelf nagaan
3.
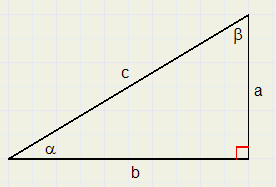
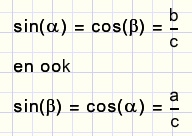
en aangezien a = 90 - b geldt dus:
-
sin (a) = cos (90 − a)
en ook
cos (a) = sin (90 − a)
Voorbeeld
Vereenvoudig de formule ...........sin( bgcos(x) )
bgcos(..) zet een getal (x) om in een hoek, sin(..) zet die hoek weer om in een getal.
Het is handig om een plaatje te tekenen van een rechthoekige driehoek met aanliggende rechthoekszijde x
en schuine zijde 1.
Dat mag, want het gaat om verhoudingen, niet om absolute groottes.
In dit plaatje is de overstaande rechthoekszijde dan gelijk aan de sinus (want schuine zijde = 1).
Volgens Pythagoras is bovenstaande formule dus te vereenvoudigen tot................\ 1 − x 2
"Mooie" hoeken
Teken een gelijkzijdige driehoek met een hoogtelijn.Hierin is te zien:
-
sin(30) = cos(60) = 0,5
-
tan(45) = 1
Aparte hoeken
Teken een rechthoekige driehoek met een hele kleine scherpe hoek en maak die hoek in gedachten steeds kleiner.Dan is te zien:
-
sin(0) = cos(90) = 0
sin(90) = cos(0) = 1
tan(0) = 0
tan(90) = .....kan niet........of: ........oneindig groot
Toepassingen
1.Draaicirkel berekenen. Kijk [ hier ]
2.
Een pont vaart met een snelheid van 8km/h over het water.
Deze pont onderhoudt de verbinding tussen de oevers van een rivier.
Die rivier is 220m. breed en de stroomsnelheid is 5km/h.
vragen:
1. onder welke hoek moet de pont varen om ondanks de stroom rechtstreeks naar de overkant te gaan?
2. hoe lang duurt de overtocht?
De route die de pont in werkelijkheid aflegt is de optelling van de stroomsnelheid en de vaarsnelheid over het water.
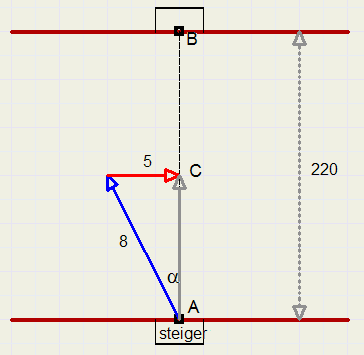
-
a = bgsin(5/8) = 38,68 graden.
AC = 8 . cos(38,68) = 6,25 (km/h)
De overtocht duurt .........0,220 / 6,25 = 0,0352 uur = 2,11 minuten.
Opgaven (10 punten per opgave)
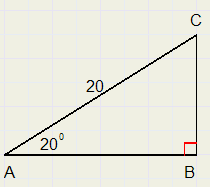
1.
2.
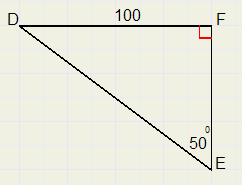
3.
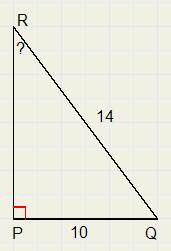
4.
5. Vereenvoudig:
-
sin(bgtan(x))
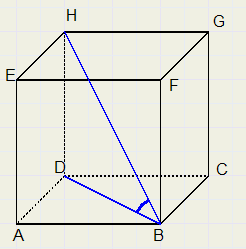
7.
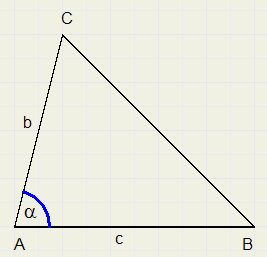
8.
Om een wiel en een paaltje P is een touw gespannen.
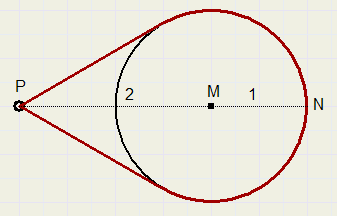
Bereken de lengte van het touw.
9.
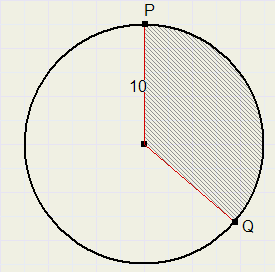
Uit een cirkelvormig stuk karton wordt een segment geknipt met een oppervlakte van 92,73 cm2
De straal van de cirkel is 10cm.
10.
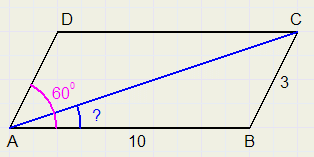
Bereken in onderstaand parallellogram LCAB
succes!
Antwoorden
1.
BC = 6,84
AB = 18,79
2.
DE = 130,5
EF = 83,9
3.
LR = 45,58 graden
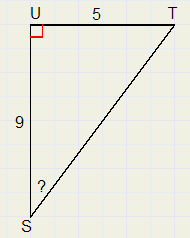
4.
LS = 29,05 graden
5.
x / W (1 + x2).............W( ) betekent wortel
6.
LHBD = 35,26 graden
7.
0,5 bc sin(a)
8.
7,65 cm.
9.
PQ = 16 m
10.
LCAB = 12,73 graden


