
 |
Cursus Algebra (4) |
 Kwadratische Functies
Kwadratische Functies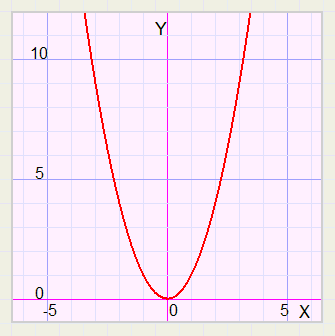 |
 |
 |
| y |
| 0,2 |
| y |
| a |
| y − v |
| a |
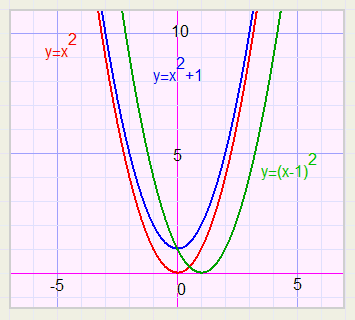
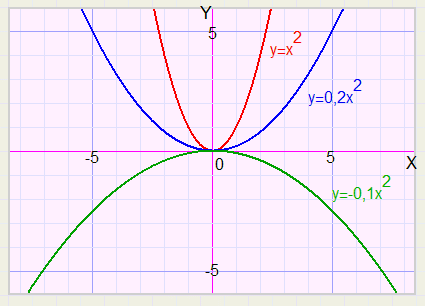
 Algemene Vormen
Algemene Vormen| −b |
| 2 a |
| −b |
| 2 a |
| 1 |
| 3 |
 Nulpunten
Nulpunten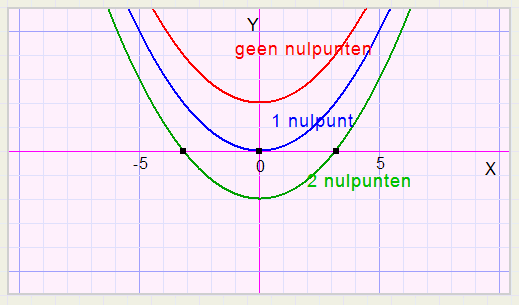 |
| \ | 5 |
| \ | 5 |
| \ | 5 |
| \ | 5 |
| \ | 5 |
 De ABC - formule
De ABC - formule| b |
| a |
| c |
| a |
| b |
| a |
| b |
| 2 a |
| b 2 |
| 4 a 2 |
| b |
| a |
| b 2 |
| 4 a 2 |
| b 2 |
| 4 a 2 |
| c |
| a |
| 2 | |||||||||
| |||||||||
| b 2 |
| 4 a 2 |
| c |
| a |
| b 2 − 4 a c |
| 4 a 2 |
| b |
| 2 a |
| ||
| 2 a |
−b +
| ||
| 2 a |
| b |
| 2 a |
−
| ||
| 2 a |
−b −
| ||
| 2 a |
| \ | d |
| −3.2 − 3.613 |
| 2 · 0.15 |
| −3.2 + 3.613 |
| 2 · 0.15 |
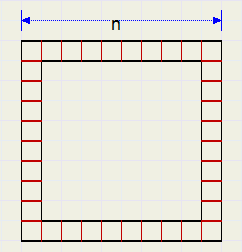 |
 Enkele voorbeelden van kwadratische verbanden
Enkele voorbeelden van kwadratische verbanden| n (n + 1) |
| 2 |
| n (n − 1) |
| 2 |
| a r n (n + 1) |
| 2 |
| K |
| n |
| K r (n + 1) |
| 2 |
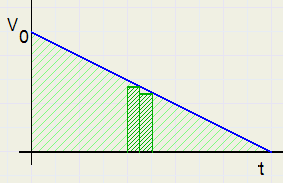 |
| V0 2 |
| 2 a |
 Verborgen Kwadratische Vergelijkingen
Verborgen Kwadratische Vergelijkingen| \ | 3 |
| \ | 7 |
| \ | s |
| \ | s |
| \ | 10 |
| a |
| x 2 |
| b |
| x |
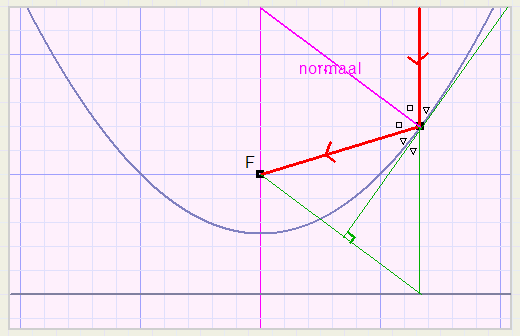
 de Parabool
de Parabool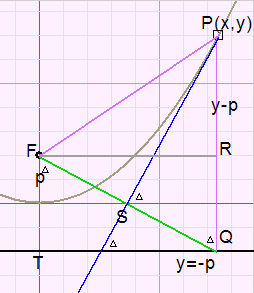 |
| x 2 |
| 4 p |
| h 2 |
| 4 p |
| T Q |
| F T |
| h |
| 2 p |
| h |
| 2 p |
| æ | x −
| ö | | |
| è | ø |
| x 2 |
| 4 p |
| h |
| 2 p |
| æ | x −
| ö | | |
| è | ø |
| h 2 |
| 4 p |
| h |
| 2 |
| h |
| 2 |
| x 2 |
| 4 p |
| x |
| 2 p |
 |
 De Cirkel
De Cirkel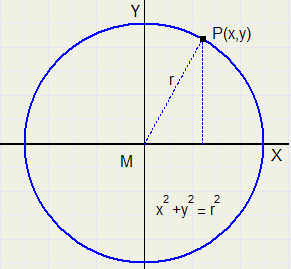 |
| \ | r 2 − x 2 |
| \ | r 2 − x 2 |
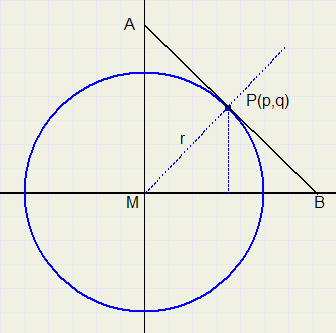 |
| −p |
| q |
| 2 | |||||||||
| |||||||||
| r 2 |
| q |
| −p |
| q |
| r 2 |
| q |
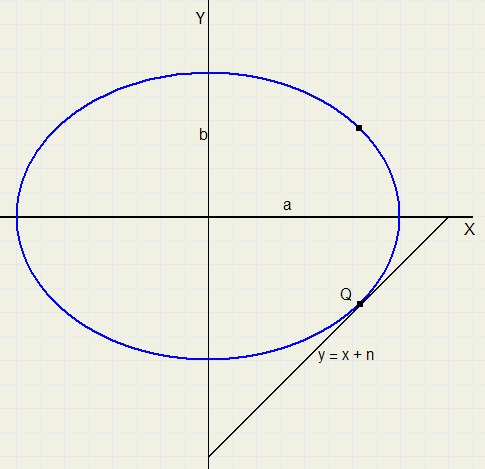
 De Ellips
De Ellips| 2 | |||||||||
| |||||||||
| 2 | |||||||||
| |||||||||
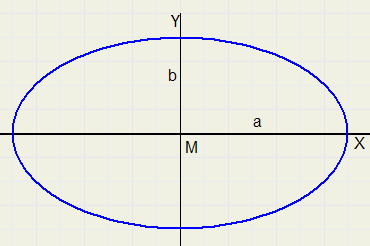 |
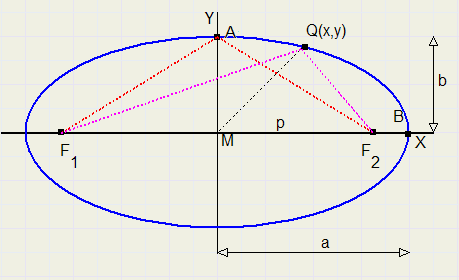 |
| \ | (p + x) 2 + y 2 |
| \ | (p − x) 2 + y 2 |
| \ | (p + x) 2 + y 2 |
| \ | (p − x) 2 + y 2 |
| \ | (p − x) 2 + y 2 |
| \ | (p − x) 2 + y 2 |
| \ | (p − x) 2 + y 2 |
| \ | (p − x) 2 + y 2 |
| 2 | |||||||||
| |||||||||
| 2 | |||||||||
| |||||||||
| \ | a 2 − b 2 |
 |
| 2 | |||||||||
| |||||||||
| 2 | |||||||||
| |||||||||
| 2 | |||||||||
| |||||||||
| 2 | |||||||||
| |||||||||
| x 2 |
| a 2 |
| x 2 + 2 n x + n 2 |
| b 2 |
| \ | a 2 + b 2 |
| \ | a 2 + b 2 |
| = | 1 |
| x 2 |
| a 2 |
x 2 − 2 x
| ||
| b 2 |
| \ | a 2 + b 2 |
| \ | a 2 + b 2 |
| a 2 |
| Q |
| b 2 |
| Q |
 Analytische Meetkunde
Analytische Meetkunde1 +
| ||
| 0.2 |
1 −
| ||
| 0.2 |
8 −
| ||
| 2 |
8 +
| ||
| 2 |
 Test
Test| 60 |
| x |
 Klik [hier]
voor een e-mail bericht met uw
Klik [hier]
voor een e-mail bericht met uw