
 |
Cursus Algebra (1) |
 Negatieve getallen
Negatieve getallen |
| fig.1 |
 |
| fig.2 |
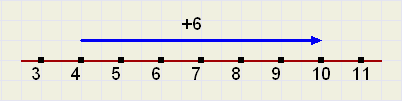 |
| fig.3 |
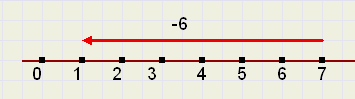 |
| fig.4 |
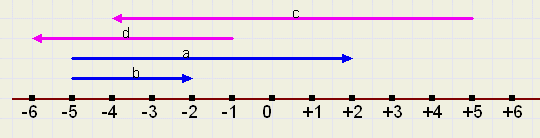 |
| fig.5 |
| regel | voorbeeld |
| + + = + | (+5) + (+4) = 5 + 4 = 9 |
| + - = - | (+5) + (-4) = 5 - 4 = 1 |
| - + = - | (+5) - (+4) = 5 - 4 = 1 |
| - - = + | (+5) - (-4) = 5 + 4 = 9 |
| a - b = a + (-b) |
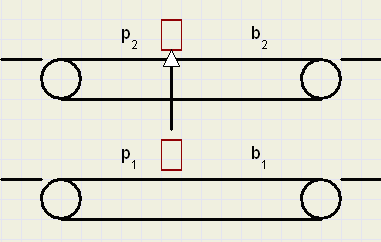 |
| fig.6 |
| 3 . (-1) = (-3) |
| 2 . (-1) = (-2) |
| 1 . (-1) = (-1) |
| 0 . (-1) = ( 0) |
| (-1) . (-1) = 1 |
| (-2) . (-1) = 2 |
 |
| fig.7 |
| regel | voorbeeld |
| + . + = + | (+5).(+4) = 20 |
| + . - = - | (+5).(-4) = (-20) |
| - . + = - | (-5).(+4) = (-20) |
| - . - = + | (-5).(-4) = 20 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
| −1 |
| 1 |
| 1 |
| 5 |
| −1 |
| 5 |
| −1 |
| 5 |
| −1 · −1 |
| −1 · 5 |
| 1 |
| −5 |
| a |
| b |
| −a |
| b |
| a |
| −b |
| regel | voorbeeld |
| + / + = + | (+10)/(+5) = 2 |
| + / - = - | (+10)/(-5) = (-2) |
| - / + = - | (-10)/(+5) = (-2) |
| - / - = + | (-10)/(-5) = 2 |
| 1 |
| 7 |
| 3 |
| 7 |
| 2 |
| 7 |
| 1 |
| 7 |
| 1 |
| 7 |
| 5 |
| 7 |
 Termen
Termen Factoren
Factoren Termen en Factoren
Termen en Factoren de Commutatieve wet (wisselwet)
de Commutatieve wet (wisselwet)| a + b = b + a |
| a.b = b.a |
 de Associatieve wet (koppelwet)
de Associatieve wet (koppelwet)| (a + b) + c = a + (b + c) |
| (a.b).c = a.(b.c) |
 de Distributieve wet (verdeelwet)
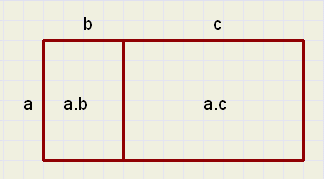
de Distributieve wet (verdeelwet)| a(b + c) = ab + ac |
| ab + ac = a(b + c) |
 Termen samenvoegen
Termen samenvoegen| de volgorde van termen mag willekeurig worden gewijzigd. |
 Factoren samenvoegen
Factoren samenvoegen| ap.aq = ap+q |
| a 5 |
| a 3 |
|
| a 7 |
| a 3 |
| k 3 |
| k |
| de volgorde van factoren mag willekeurig worden gewijzigd |
 Een uitbreiding van de distributieve wet
Een uitbreiding van de distributieve wet Formules met termen verbouwen
Formules met termen verbouwen| 9 + 4 + 7 | = | 15 + 5 |
| 9 + 4 + 7 + 100 | = | 15 + 5 + 100 |
| termen mogen over het "=" teken worden getild als hun teken wordt omgedraaid |
 Formules met factoren verbouwen
Formules met factoren verbouwen| p q |
| b |
| 1 |
| b |
| 1 |
| b |
| p q |
| b |
| 1 |
| b |
| b |
| 1 |
| 1 |
| b |
| b |
| b |
| factoren mogen over het "=" teken worden getild als teller en noemer van plaats wisselen. |
| p |
| 1 |
| v w |
| x y |
| v w |
| y |
| v w |
| b y |
| v w |
| b y a |
| H.P |
| R |
| = |
|
| I.R |
| P T |
 Rekenregels vs. Vergelijkingen.
Rekenregels vs. Vergelijkingen. Voorbeeld
Voorbeeld| 3 |
| 7 |
| 10 |
| 7 |
| 7 |
| 10 |
| 10 |
| 7 |
| 7 |
| 10 |
| 3 y − 10 |
| 12 − y |
| 12 x + 10 |
| x + 3 |
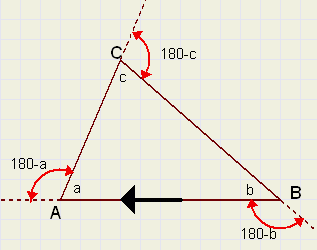 |
| figuur 8. |
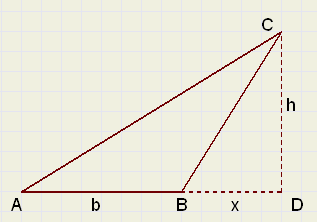 |
| figuur 9. |
| (b + x) h |
| 2 |
| x h |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| b h |
| 2 |
einde algebra deel 1
 Test
Test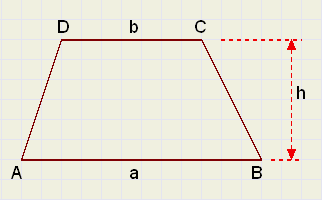 |
| figuur 10. |
 Klik hier
voor een e-mail bericht met uw
Klik hier
voor een e-mail bericht met uw