
 |
Cursus Algebra (3) |
 Inleiding
Inleiding Het Rechthoekig Co÷rdinatenstelsel
Het Rechthoekig Co÷rdinatenstelsel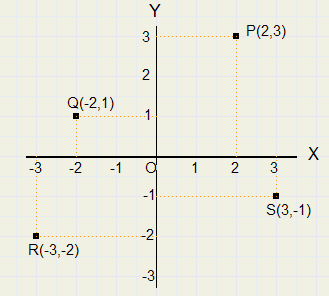 |
 Lijnen evenwijdig aan de assen
Lijnen evenwijdig aan de assen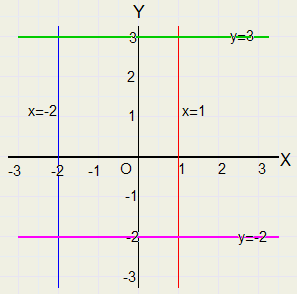 |
 De afstand van twee punten
De afstand van twee punten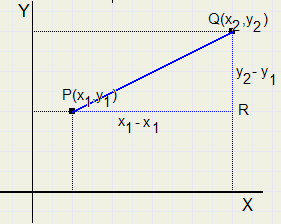 |
| \ | (x2 − x1) 2 + (y2 − y1) 2 |
| \ | (16 − 4) 2 + (14 − 9) 2 |
| \ | (2 − −5) 2 + (−19 − 5) 2 |
 Lijnen door de oorsprong
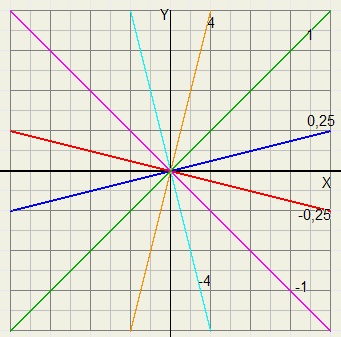
Lijnen door de oorsprong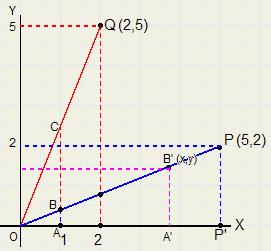 |
| y |
| x |
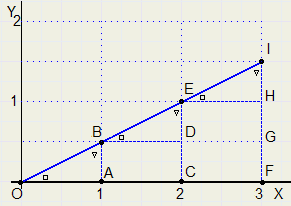 |
| y |
| x |
| 1 |
| 2 |
| A B |
| O A |
| D E |
| B D |
| C E |
| O C |
| F I |
| O F |
 |
 Loodrecht
Loodrecht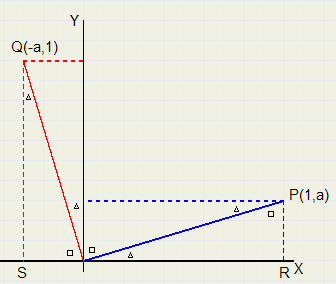 |
 Lijn door 2 punten
Lijn door 2 punten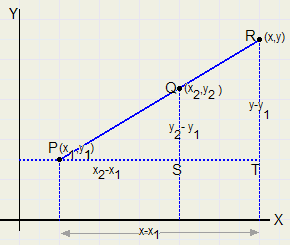 |
| y − y1 |
| x − x1 |
| y2 − y1 |
| x2 − x1 |
| y2 − y1 |
| x2 − x1 |
| 17 − 5 |
| 20 − 10 |
| −2 − 8 |
| 7 − 5 |
 Afstand Punt tot Lijn
Afstand Punt tot Lijn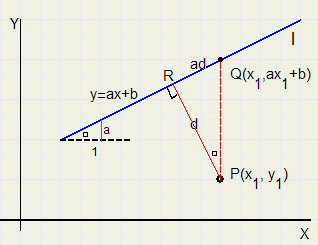 |
| P Q | ||
|
| 9 | ||
|
| \ | 10 |
 Afstand tussen Evenwijdige Lijnen
Afstand tussen Evenwijdige Lijnen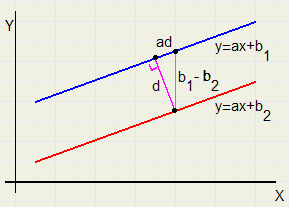 |
| d | = |
|
 Het Snijpunt van twee Lijnen
Het Snijpunt van twee Lijnen| b2 − b1 |
| a1 − a2 |
 Vergelijkingen, Functies en Grafieken.
Vergelijkingen, Functies en Grafieken. Verschuiven
Verschuiven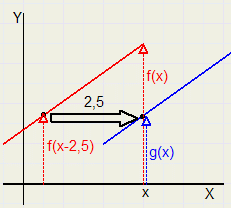 |
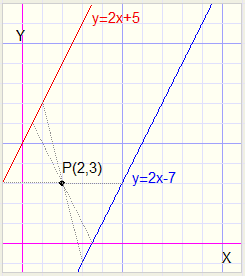
 Spiegelen
Spiegelen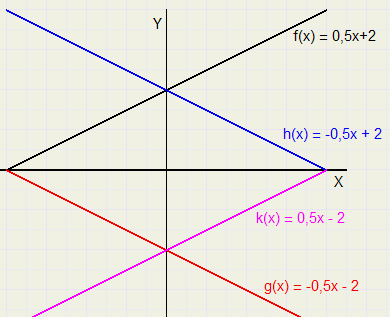 |
 |
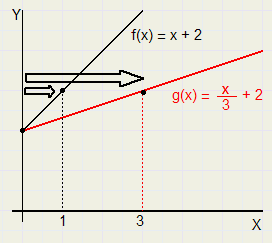
 Uitrekken
Uitrekken| x |
| 3 |
| x |
| 3 |
| x |
| 3 |
| x |
| 3 |
 |
 Lijnen Roteren
Lijnen Roteren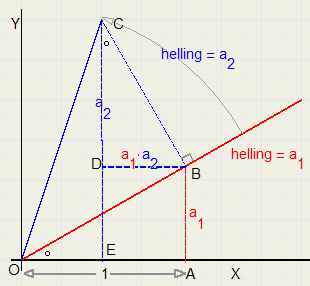 |
| O B |
| O A |
| B C |
| D C |
| B C |
| O B |
| a2 (O B) |
| O B |
| a1 + a2 |
| 1 − a1 a2 |
| a1 + a2 |
| 1 − a1 a2 |
| 2 + 1.732 |
| 1 − 2 · 1.732 |
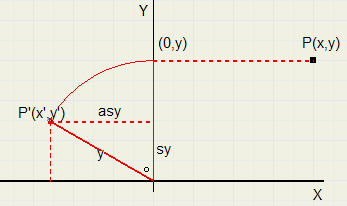
 Een Punt Roteren
Een Punt Roteren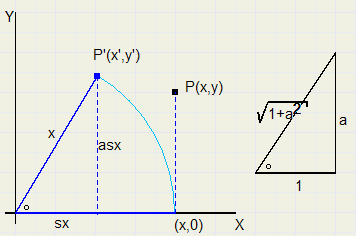 |
| s | = |
|
 |
| a | ||
|
 Test
Test Klik [hier]
voor een e-mail bericht met uw
Klik [hier]
voor een e-mail bericht met uw