|
Tellen & Talstelsels (3) |
 |
Inhoud:
[1] tellen
[2] modulus rekenen
[3] gekoppelde tellers
[4] een gerobotiseerd onderdelen magazijn
[5] talstelsels
[6] negatieve getallen
[7] som, verschil, complement
[8] antwoorden
Tellers koppelen
Hieronder zie je twee gekoppelde tellers staan.
Met de uitgaande pijl geeft T0 een zg. carry-signaal door als T0 over de kop gaat.
Zodoende wordt T1 elke keer verhoogd als T0 over de kop gaat.
vraag 4
a. wat is de modulus van T0 en T1 samen?
b. bereken de standen van T0 en T1 als 25 maal is verhoogd na reset (N = 25)
c. T0 = 3, T1 = 2. Bereken N.
d. bereken T0 en T1 als N = 4455
Stel eens, dat T0 een modulo 60 en T1 een modulo 12 teller is
e. bereken de stand als N = 1000
Een klok met wijzers geeft 9 uur aan
f. bereken de tijd over 5000 minuten
g. wat wordt de modulus van de gehele teller als T0 mod m1 en T1 mod m2 telt?
Hieronder tref je drie gekoppelde tellers aan.
vraag 5
a. wat is de modulus van T0,T1 en T2 samen?
b. bereken de standen van T0,T1,T2 als N = 31
c. T0 = 3, T1 = 2, T2 = 1. Bereken N.
Stel, dat N = 5678
d. bereken T0,T1,T2
e. hoe vaak is T0 over de kop gegaan?
f. en T1?
g. en T2?
h. en het gehele telwerk?
stelling:
De modulus m van een telwerk, dat bestaat uit tellers met modulus m1 , m2 , m3... is
m = m1 * m2 * m3 * ................
Je hebt dit waarschijnlijk al zelf beredeneerd.
Toepassingen van telwerken
1.Coderen
Coderen is het verstoppen van eigenschappen of omstandigheden in een getal.
Bij een bepaald merk auto heeft de koper de keuze uit verschillende kleuren,
uitvoeringen of type motor.
We willen die keuzen (de bestelling) in 1, zo klein mogelijk, getal vastleggen.
In het geval van deze auto wordt afgesproken:
| kleur | rood | 0 |
| wit | 1 |
| blauw | 2 |
| groen | 3 |
| uitvoering | 3 deurs | 0 |
| 5 deurs | 1 |
| station | 2 |
| brandstof | benzine | 0 |
| diesel | 1 |
Aan de kleur koppelen we een teller, met bereik 0..3
Aan de uitvoering een teller met bereik 0..2 en
de keuze van brandstof wordt met een teller met bereik 0..1 weergegeven.
Die tellers zijn gekoppeld en zijn, voor dit geval, precies gelijk aan het
telwerk boven vraag 5.op deze pagina.
Bij elke stand van dit telwerk (d.i. een bestelling) hoort een waarde van N.
N is de gecodeerde keuze, waarin dus alle eigenschappen zijn opgeborgen.
Opmerking: een code omrekenen naar bestelling heet decoderen.
Dat decoderen is natuurlijk alleen mogelijk als de afspraken bekend zijn.
2.Tabellen
Hieronder zie je een tabel met 5 kolommen (0..4) en 4 rijen (0..3).
Er zijn dus 20 velden, genummerd 0..19.
| rij / kolom | 0 | 1 | 2 | 3 | 4 |
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 5 | 6 | 7 | 8 | 9 |
| 2 | 10 | 11 | 12 | 13 | 14 |
| 3 | 15 | 16 | 17 | 18 | 19 |
Door de het kolomnummer (0..4) en het rijnummer (0..3) op te vatten
als een telwerk, is het veldnummer te berekenen.
Omgekeerd kan, uitgaande van het veldnummer, de rij en de kolom worden berekend.
Merk op, dat dit telwerk overeenkomt met het telwerk bovenaan deze pagina.
T0 telt dan de kolommen, T1 de rijen en N is het veldnummer.
Dergelijke omrekeningen komen veel voor. In een computergeheugen liggen de getallen
"achter elkaar", als in een tabel met slechts 1 kolom.
Om toch een tabel met rijen en kolommen weer te geven, moeten berekeningen als
hierboven plaatsvinden.
3.Plaatsbepaling in Computer-Window
Het volgende voorbeeld komt veelvuldig voor bij het programmeren van spelletjes.
In een window is een speelbord afgebeeld, dat is opgedeeld in rechthoeken.
Die rechthoeken zijn vergelijkbaar met de velden in de tabel hierboven.
In sommige velden is het nummer afgebeeld.
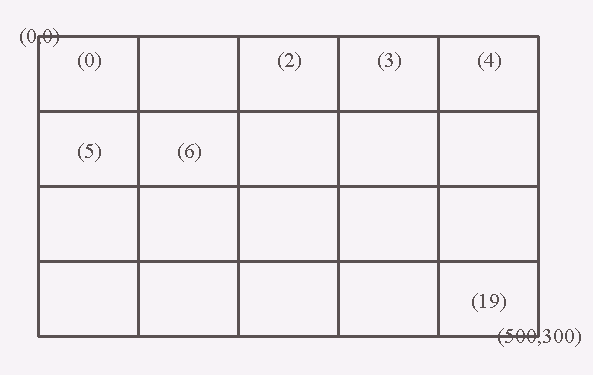
Zie het plaatje hieronder:
Een computerscherm is opgebouwd uit puntjes, die pixels worden genoemd.
Een schermresolutie van 600*800 wil zeggen, dat er 600 rijen zijn met elk 800 pixels.
Per pixel staat in het video-geheugen een gecodeerd getal, dat de kleur aangeeft.
Merk op, dat coördinaten (0,0) linksboven en (500,300) rechtsonder staan,
zoals gebruikelijk bij computerschermen.
Elk veld is hier 100 pixels breed en 75 pixels hoog.
Nu het probleem:
Als we met de muis over het window bewegen, dan levert het programma (Windows)
per muisbeweging de coördinaten (x,y) van de cursorpijl.
De programmeur wil alleen weten, op welk veld de cursor zich bevindt.
Dat kan al volgt worden bepaald:
x div 100 levert het nummer K van de kolom op
y div 75 geeft het nummer R van de rij
K + 5*R levert het veldnummer op
opmerking: x mod 100 geeft de relatieve horizontale positie in een veld
stel, dat de programmeur het rechthoekje van veld 17 opnieuw wil tekenen.
Dan moeten eerst de coördinaten (x,y) worden berekend.
Daarvoor moet de kolom K en de rij R worden bepaald.
K = 17 mod 5 = 2. Dus x = 2*100 = 200
R = 17 div 5 = 3. Dus y = 3* 75 = 225
De coördinaten van veld 17 (linksboven) zijn (200,225).
merk op: omzetting van pixelcoördinaten (x,y) naar veldcoördinaten (K,R)
is vergelijkbaar met omlaag afronden op respectievelijk 100- en 75-tallen.
4.Formatteren van output
Een computerprogramma drukt een groot aantal getallen af.
Per regel 12 getallen. En elke vijfde regel moet een iets donkerder achtergrondkleur
krijgen voor de duidelijkheid.
De oplossing is per getal een teller N bij te houden.
Getallen worden per regel achter elkaar afgedrukt.
Na elk getal wordt N verhoogd.
Als N mod 12 = 0, dan wordt naar een nieuwe regel gesprongen.
Als N mod (5*12) = 0, dan wordt de achtergrondkleur iets donkerder gemaakt.