priemgetallen puzzel

Priemgetallen puzzeltje

download programma

download Delphi-7 project

Dit priemfetallen puzzeltje trof ik aan op Facebook.

"Wat is het grootste priemgetal dat je kunt maken door de cijfers 1..9 niet meer dan eens te gebruiken"

In dit artikel beschrijf ik een Delphi programma dat deze puzzel oplost.
Ziehier het resultaat:

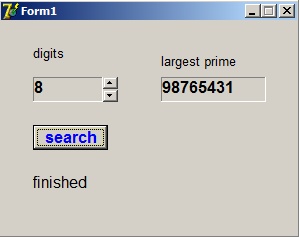
Opmerking:
Voor wat theorie verwijs ik naar
the basic theory of counting and coding (Engels) of
tellen en talstelsels

Een getal dat alle cijfers van 1 to 9 bevat kan geen priemgetal zijn.
De som van de cijfers is dan 45 wat deelbaar is door 3 dus is het getal ook deelbaar door 3.
Onze zoektocht begint dus met getallen van 8 cijfers.

Ik heb het wat breder aangepakt:
"zoek het grootste priemgetal van k cijfers waarin een cijfer maar één keer voorkomt".

Er zijn verschillende manieren om keuzes uit cijfers (of objecten) te maken.
In dit geval is de volgorde belangrijk want het getal 123 is ongelijk aan 321.
Ook mag een cijfer maar één maal gekozen worden.
Zo'n keuze heet een variatie.

Hoe lossen we dit probleem op met een (Delphi) programma dat het werk doet?
Het project heeft drie delen:

1. genereer een nieuw getal dat mogelijk priem is.
2. test dit getal op priem eigenschap.
3. herhaal stappen 1. en 2. en rapporteer de resultaten

1.
Aan een variatie kunnen we een rank (volgorde nummer) toekennen.
Met het ophogen van de rank genereren we dan systematisch een nieuwe variatie van cijfers, dus een nieuw getal.
Voor k = 3 (3 cijfers) loopt de rank van 0 tot 9*8*7 - 1 = 503.

Het getal behorende bij rank 0 is 123, rank 1: 124....rank 503: 987.

Hoe maak je het getal bij een rank?
Array elements bevat bij de start de cijfers 1..9.
Element[1] = 1...Element[9] = 9.
Voor de eerste keuze zijn er 9 mogelijkheden (cijfers 1..9) en de keuze is (rank mod 9).
Dit getal heet digitnumber en loopt van 0..8 dus moet 1 worden opgeteld omdat we de elementen tellen van 1..9.
Ons cijfer wordt: element[digitNr].

Het geselecteerde cijfer moet nu uit het elements array verwijderd worden.
Dat doen we door de volgende cijfers omlaag te schuiven.
De rank wordt nu verlaagd: Rank = Rank div 9.

Het volgende cijfer: digitNr = (Rank mod 8) + 1 omdat uit 8 resterende elementen wordt gekozen.
Opnieuw is digit = element[digitNr] en ook dit element wordt verwijderd door omlaagschuiven van de volgende cijfers.
Rank = Rank div 8.

Daarna: digitNr = (Rank mod 7) + 1.
Digit = element[digitNr]
en de drie cijfers zijn gekozen.

Om het getal te maken moeten de gekozen cijfers met 1,10,100 vermenigvuldigd worden en opgeteld.

Deze Delphi functie doet het werk:

function variation(rank : dword; k : byte) : dword;
//rank is sequence nr of variation of k digit selection 1..9
//result is made of choosen digits
var element : array[1..9] of byte;
    decexp : dword;//decimal exponent
    i,j,digit,digitnr : byte;
begin
 for i := 1 to 9 do element[i] := i;  //reset elements
 decexp := 1;
 result := 0;
 for i := 1 to k do
  begin
   digitnr := (rank mod (10-i)) + 1;
   rank := rank div (10-i);
   digit := element[digitnr];
   result := result + decexp*digit;
   for j := digitnr to 8 do element[j] := element[j+1];
   element[9] := 0;
   decexp := decexp*10;
  end;
end;

Schematische weergave:

2.
Een getal testen op de priem eigenschap.
Zes opvolgende getallen zijn te schrijven in de vorm: 6k, 6k+1,...,6k+5 waarbij k=1,2,3,4.....
Alleen de getallen van de vorm 6k+1 en 6k+5 kunnen priem zijn.
6k is deelbaar door 2 en 3, 6k+2 is deelbaar door 2, 6k+3 door 3 en 6k+4 door 2.
We hoeven dus alleen de gevallen 6k+1 en 6k+5 te onderzoeken.

Priemgetallen bevatten geen (priem) factoren.
Een priemgetal is geen veelvoud van een ander getal.
Delingen door andere getallen mogen dus nooit als rest 0 opleveren.
Die delers kunnen we ook beperken tot getallen die voldoen aan 6k-1 en 6k+1.
Dat doen we door de delers om en om met 2,4,2,4 te verhogen.

Deze functie doet het werk:

function prime(Pnr : dword) : boolean;
//return true if Pnr is prime
//primes have format 6K-1 or 6K+1
var treshold : dword;
    divisor : dword;
    divincr : byte;
begin
 treshold := round(sqrt(Pnr));
 result := ((Pnr mod 3) > 0) and ((Pnr mod 5) > 0);
 divisor := 5;
 divincr := 2;
 while (result) and (divisor < treshold) do
  begin
   divisor := divisor + divincr;
   divincr := 6 - divincr;
   result := (Pnr mod divisor) > 0;
  end;
end;

Een andere truuk om het proces wat te versnellen is om alleen delers te gebruiken die
kleiner zijn dan de wortel uit het getal.
Dat is logisch als we bedenken dat a*b = b*a.
Als Getal / a = b dan is natuurlijk Getal / b = a.
Maar als b > a dan voegt de deling Getal / b niets nieuws toe.

3.
Bovenstaande functies aanroepen en resultaat tonen:

procedure TForm1.BitBtn1Click(Sender: TObject);
//search largest prime 
var i : byte;
    maxvar : dword;
    varnr : dword;
    N : dword;    
    oldprime : dword;
    digitcount : byte;
begin
 digitcount := updown1.Position;
 oldprime := 2;
 label3.Caption := 'searching';
 statictext2.Caption := 'no primes';
 application.ProcessMessages;
 maxvar := 1;
 for i := 1 to digitcount do maxvar := maxvar * (10-i);
 varnr := 0; //rank of variation
 repeat
  N := variation(varnr,digitcount);
  if ((N+1) mod 6 = 0) or ((N-1) mod 6 = 0) then
   if prime(N) then
    if N > oldPrime then
     begin
      oldPrime := N;
      statictext2.Caption := inttostr(N);
     end;
  inc(varnr);
 until varnr = maxvar;
 label3.Caption := 'finished'; 
end;

variabelen:

Controls: