A basic theory of coding and number systems

Counting

Counting has started most likely as shown below:



For large numbers and calculations this notation is inconvenient.
Number systems are much more efficient.
How does a number system evolve?
Below is pictured a basic counter building block:



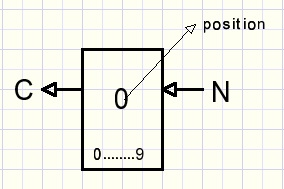
This small counter may be contructed of mechanics, electronis or whatever.
A signal (pushbutton, handle) increments the counter by 1.
N is the number of increments.
The counter has a limited number of positions, here 0..9.
So, after 9 increments (from 0) it's position is 9 and the next increment
sets the counter position at 0 because it is a rotating device.
While switching from 9 to 0 a carry or overflow signal C is generated.

Question 1:
what is the position of the counter after N increments (from 0)?
This calculation is written as
    N mod 10
mod stands for modulus.
The modulus of a counter is the total number of positions (0..9)
We show here a modulo 10 counter.

Examples:
    11 mod 10 = 1
    197 mod 10 = 7
The modulus (10) is the remainder after integer division of N by 10.

Question 2:
How many carries do we generate after N increments?
This calculation is written as
    N div 10
div stands for integer division, digits in the quotient behind the decimal point are discarded.
Examples:
    7 div 10 = 0
    27 div 10 = 2
Notice: N = (N mod m) + (N div m)*m for integers N,m

To calculate N div m using a pocket calculator:
    1. calculate N : m
    2. discard digits behind decimal point.
Example: 123 : 44 = 2.795
123 div 44 = 2

To calculate N mod m using a pocket calculator:
    1.calculate N : m
    2.subtract integer part N div m
    3.multiply by m
Example:
    123 : 44 = 2.795
    0.795 * 44 = 35
    123 mod 44 = 35
check: 123 = 2*44 + 35 ....OK

A number system appears when these simple counter blocks are combined:



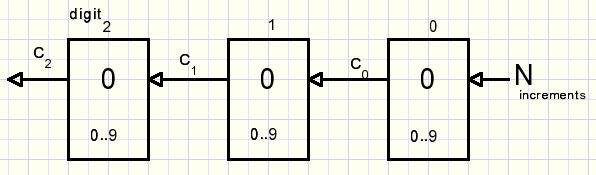
We see:
    C0 = N div 10
    C1 = C0 div 10
    C2 = C1 div 10
    digit 0 = N mod 10
    digit 1 = C0 mod 10
    digit 2 = C1 mod 10
The modulus of the counter building blocks defines the number system.
Simply set m to 2 in calculations N mod m , N div m and the binary system results.

Rules


(N+P) mod m = (N mod m) + (P mod m)
(N*P) mod m = (N mod m)*(P mod m)

The proof is left to the reader.

Application

The 3 divisor proof of divisibility.
If the digits of a decimal number add up to a multiple of 3, then this number is divisible by 3.
Proof:
A number N is divisible by 3 if N mod 3 = 0
Say number N has digits dcba so it's value is 1000d + 100c + 10b + a
(1000d + 100c + 10b + a) mod 3 =
(1000d mod 3) + (100c mod 3) + (10b mod 3) + (a mod 3) =
(1000 mod 3)(d mod 3) + (100 mod 3)(c mod 3) + (10 mod 3)(b mod 3) + (a mod 3)=
1(d mod 3) + 1(c mod 3) + 1(b mod 3) + (a mod 3) =
(d + c + b + a) mod 3.

Rules

1.
Two combined mod m counters behave as one mod m2 counter.

Now consider a counter with number base m and digits dn...d1 d0.

2.
The value N of this counter is dn * mn + .... + d1 * m1 + d0 * m0.
If a counter value is N then
    d0 = N mod m
    d1 = (N div m) mod m
    dn = (N div mn) mod m
3.Number system conversion of integers
To write value N in a number system base m:
    1. N mod m provides the least significant digit
    2. N div m removes the least significant digit
    3. repeat steps 1,2 until N = 0
4.Number system conversions of fractions (decimal point assumed left of number)
To write fraction in number system base m:
    1. N = N * m makes the left digit integer.
    2. remove and save integer part
    3. repeat steps 1,2 until N = 0

Coding

So far, all counter blocks had the same modulus resulting in a number system.
However, we may assign each counter block position a certain choice.
The modulus is the number of choices.
For multiple choices counter blocks are combined.
A combination of choices (so positions of the digits) requires a certain unique number
of increments N at the input of digit 0.
So, N may be regarded as a code that stands for the counter block positions.

Example:
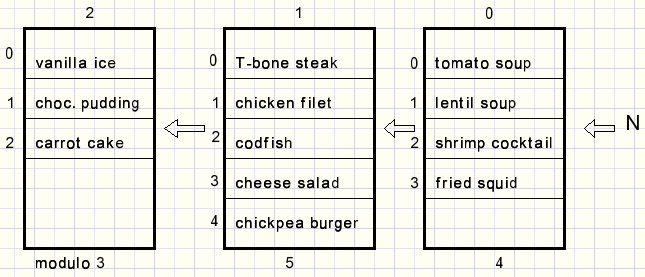
We visit a restaurant which has following choices
    starter: tomato soup, lentil soup, shrimp cocktail, fried squid.
    main dish : T-bone steak, chicken filet, fried codfish, cheese salad, chickpea burger.
    dessert : vanilla ice cream, chocolate pudding, carrot cake.
Counter 0 handles the starter choices 0..3 (0: tomato soup.....3: fried squid) modulus = 4.
Counter 1 handles the main dish choices 0..4 (0:T-bone....4:chickpea) modulus = 5.
Counter 2 handles the desserts 0..2 (0:ice...2:cake) modulus = 3.

Say a visitor orders lentil soup, cheese salad and carrot cake.
Which number (N) codes this choices?

Counters 2,1,0 hold number 231.
Counter 2 position 2 requires 2 carries from counter 1 which requires 10 carries out of counter 0
which requires 4*10 = 40 increments into counter 0.
Position 3 of counter 1 required 4*3 = 12 increments into counter 0.
Position 1 of counter 1 required 1 increment.
N = 40 + 12 + 1 = 53.
53 is the unique code for this choice.

Check:
53 mod 4 = 1. (lentil soup starter)
53 div 4 = 13.
13 mod 5 = 3 (cheese salad main dish)
13 div 5 = 2 (carrot cake dessert)



Note:
Alway count choices starting with 0.

This way of coding a situation into a number applies to many cases such as
    - addresses in an appartment building
    - location of parts in a warehouse
so, any case in which several independent choices have to be made.