3D Lissajous figuren tekenen

Met het (Windows) programma lissajous3d kan je drie dimensionale Lissajous figuren tekenen.
Hieronder staat een voorbeeld:
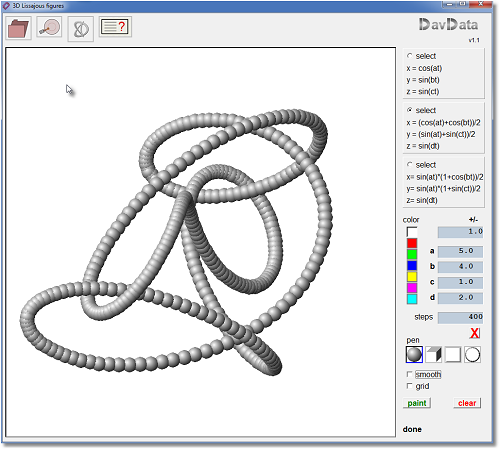
Klik op het download (bliksem) icoontje bovenaan deze bladzijde om het programma te downloaden.

Wat kan het programma?

    - keuze uit 3 sets Lissajous formules
    - keuze uit 4 pen stijlen:
      - bol
      - kubus
      - vierkant
      - cirkel
    - keuze uit 7 kleuren
    - enkele of verbonden punten (smooth)
    - stap waarde van 100..1000
    - instellingen (figuur) bewaren (*.l3d file extensie)
    - instellingen laden
    - figuur opslaan (*.bmp extensie)
Selections zijn te maken met muiskliks.
Voor de constanten a,b,c,d geldt:
- een linkerklik telt de (+/-) waarde bij
- een rechterklik trekt de (+/-) waarde af.
De (+/-) waarde zelf kan ook met muiskliks worden veranderd.

Interim variabele t telt van 0 tot het aantal stappen. ( stepcount).
Stepcount is instelbaar van 100 tot 1000 in stappen van 50.

De menuknoppen wijzen verder zichzelf.

Hieronder twee keer hetzelfde plaatje, wel en niet "smooth" afgebeeld
    punt voor punt smooth

Wat zijn Lissajous figuren?

Gewone functies hebben dit formaat:
    y = ... x ..., waarbij de ... staan voor constanten en operatoren.
Bij het tekenenen van de grafiek ontstaat een vloeiende lijn.
Voor een waarde van x levert de functie één waarde van y.
Het tekenen van cirkels, ellipsen of spiralen is dus niet mogelijk.

Die beperking bestaat niet als we parameter functies gebruiken, die hebben het formaat
    x = ...t...
    y = ...t...
Nu zijn x en y beide een functie van interim variabele t.

Lissajous functies hebben de vorm:
    x = cos(...t)
    y = sin(...t)
x en y zijn beide periodieke functies van t.
Opmerking: sin en cos zijn inwisselbaar.

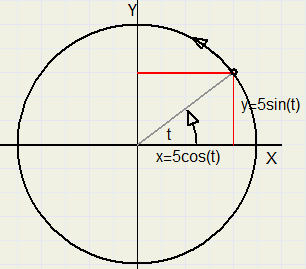
Een cirkel met straal 5 en middelpunt (0,0) wordt weergegeven door:
    x = 5cos(t)
    y = 5sin(t)
Hoeken worden gemeten in graden, maar interne berekeningen gaan in radialen. 2p radialen = 360 graden.
360 graden vormen één periode.
In het plaatje hieronder moet t dus van 0 tot 360 verhogen om de hele cirkel te tekenen.
Interessantere plaatjes ontstaan door constantes in te voeren of zelfs periodieke functies op te tellen
of te vermenigvuldigen.
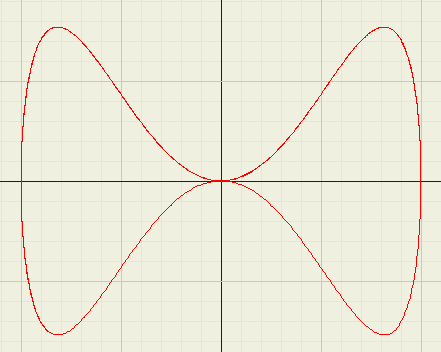x = 2cos(t)
y = sin(t) + sin(3t)

Het plaatje hierboven is gemaakt met het grafieken programma graphics explorer.

Lissajous 3D

Voor 3D grafieken moet een z as worden toegevoegd aan het X Y coördinaten stelsel.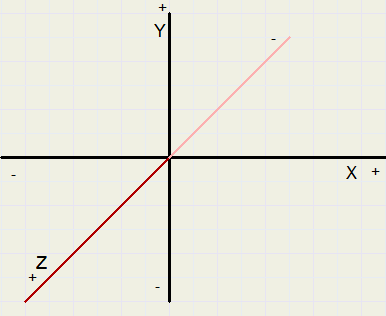
3D Lissajous functies hebben de algemene vorm:
    x = cos(..t)...
    y = sin(..t)...
    z = sin(..t)...
Opmerking: sin en cos functies zijn onderling verwisselbaar.
Het plaatje bovenaan deze bladzijde is onstaan met
    x = 0.5cos(5t) + 0.5cos(4t)
    y = 0.5sin(5t) + 0.5sin(t)
    z = sin(2t)
Waarbij t telt van 0 tot 400.
Voor elke waarde van t wordt een bolletje getekend.

Meer informatie

Klik [hier] voor meer informatie over dit Delphi programmeer project.
Daarin staat ook een link naar de complete source code.
Klik op het download (bliksem) icoontje bovenaan de bladzijde om dit (Windows) programma te downloaden.

Veel plezier!