Lissajous figures tekenen Er is ook een 3D Lissajous programma. Kijk hier . Inleiding. Lissajous (1822...1880) was een Frans wiskundige, die bekend is van zijn onderzoek aan trillingen en golven. In dit artikel wordt beschreven hoe je, met behulp van Graphics-Explorer bewegende Lissajous figuren kunt maken. Theorie. Het plaatje hiernaast is afgeleid van zg."Lissajous" figuren. Lissajous figuren maak je met zg. "parameter" functies. Bij "gewone" functies als y = 5sin(x), levert één waarde van x steeds (hoogstens) één waarde van y op. Het is dus niet mogelijk spiralen of andere in elkaar gedraaide grafieken te maken. Ook de grafiek van een cirkel kan niet met een gewone functie worden verkregen. Met parameter functies kan dat wel, door de volgende truc: in plaats van y = f(x) schrijven we y = g(v) en x = h(v) dus zowel x als y zijn nu functies van v geworden. Opmerking: vaak wordt de letter t gebruikt, maar Graphics-Explorer gebruikt de v in parameter functies. Als bijvoorbeeld y = 5sin(v) en x = 5cos(v) en v doorloopt de waarden 0..6,28 ( 2*p) dan is de grafiek een cirkel met middelpunt (0,0) en een straal van straal 5. Algemeen: Een Lissajous-figuur ontstaat, als in een parameterfunctie zowel x als y een cyclische functie is van v Gemolesteerde Lissajous figuren. Zo kan je het bewegende plaatje bovenaan deze page aanduiden. Lissajous-figuren zullen altijd een vloeiend verloop hebben. Immers, ook de grafiek van een gewone functie vertoont geen knikken. Dat de grafiek wel knikken vertoont, komt door het (te) geringe aantal stappen van v. Daardoor verloopt de grafiek sprongsgewijs in plaats van vloeiend. Graphics-Explorer gaat namelijk bij het tekenen van parameter-functies als volgt te werk: 1. bepaal stapgrootte van v = (eindwaarde - beginwaarde)/aantal stappen 2. bereken (x,y) coördinaten voor beginwaarde van v 3. verhoog v met de stapwaarde 4. bereken opnieuw (x,y) en trek een rechte lijn naar de vorige (x,y) coördinaten 5. herhaal stappen 3. en 4 tot de eindwaarde is bereikt Bij te grote stappen ontstaan nu geknikte rechte lijnen in plaats van vloeiende curven. Praktijk. Start het grafieken programma Graphics-Explorer Tik in : y = 5sin(a*v) ; x = 5cos(b*v) Selecteer: 'vervangen' en 'autoplot' en druk [enter] Zet de beginwaarde op 0, de eindwaarde op 10 en het aantal stappen op 200. Door de linker- of rechter-muisknop boven de constanten a en b ingedrukt te houden wijzigen de constanten en de grafiek past zich aan. Varieer de +/- stapgrootte van de constanten voor de gewenste nauwkeurigheid. Ook kan je invoeren: y = c*sin(a*v) ; x = c*cos(b*v) dan is met de constante c de grootte van de grafiek in te stellen. 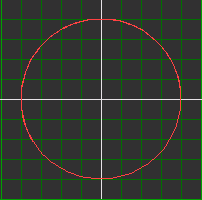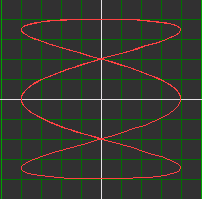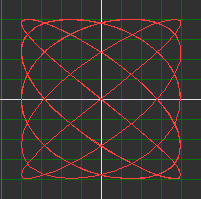Enkele voorbeelden: y = 4sin(a*v) ; x = 4cos(b*v) v : start=0 einde=10 aantal stappen=200 a=1 b=1 a=1 b=3 a=4 b=5 Spirografen. Fraaie figuren zijn te verkrijgen door een punt over een cirkel te laten bewegen, maar dit punt weer als middelpunt van een tweede cirkel te beschouwen. Een punt bewegend over die tweede cirkel is dan de 'pen'. tik in: y = 5sin(a*v) + c*sin(b*v) ; x = 5cos(a*v) + c*cos(b*v) De grootte van a bepaalt de snelheid waarmee de tweede cirkel over de eerste beweegt en b bepaalt de snelheid van de pen over de tweede cirkel. C is de straal van die tweede cirkel. Door a,b en c in 'autoplot' mode te wijzigen, maak je een film van spiralen. 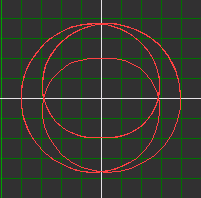y = 3sin(a*v)+c*sin(b*v) ; x = 3cos(a*v) + c*cos(b*v) v : start=0 einde=10 aantal stappen=100 a=3 b=5 c=1 a=5,2 b=26 c=1,7 a=9,5 b=67,94 c=1 Een ander voorbeeld: Type: y = c*sin(a*v)(1 + sin(b*v)) ; x = c*cos(a*v)(1 + sin(b*v)) Een punt beweegt over een cirkel met snelheid a (radialen/v). De straal van de cirkel wordt gemoduleerd met de factor (1 + sin(b*v)). 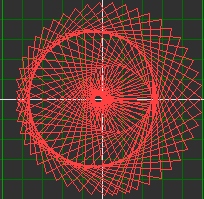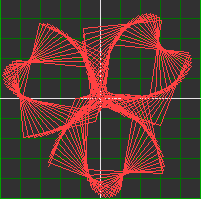y = c*sin(a*v)(1 + sin(b*v)) ; x = c*cos(a*v)(1 + sin(b*v)) start = 0 end = 10 steps = 200 A=29,82 B=11.88 C=2,5 A=100 B=25 C=2,5 A=18 B=27,1 C=2,5 Verschillende kleuren en formules kunnen worden gecombineerd voor nog wildere figuren. Het bewegende plaatje bovenaan deze page is gemaakt door de grafiek eerst op het klembord te zetten (menu:algemeen:bewaren:grafieken:klembord) en dan te plakken in het freeware programma Formati. Hiermee kan het plaatje worden bijgeknipt en een GIF afbeelding gemaakt. Deze GIF afbeeldingen zijn daarna in het (eveneens freeware) programma UnFREEz gesleept, dat er een animated GIF van maakt. Succes gewenst! Opmerking Beeldend kunstenares Jennifer Townley bouwt o.a. een machine die Lissajous figuren tekent. Kijk [HIER] op haar website.