

 |
De Kortste Zijde. |  |
 |
Onderstaand probleem ging aanvankelijk uit van een scherpe hoek, wat moeilijk bleek.
De oplossing was achteraf ook niet correct, zodat het eenvoudiger geval
van een rechte hoek werd gekozen.
Het originele probleem met de foute oplossing is [ HIER ] nog te vinden.
Recent (18 jan. 2019) ontving ik echter van Hans Sellmeijer een indrukwekkende oplossing.
Het is een analytische aanpak. Kijk [ HIER ]
Het probleem
Zie figuur 1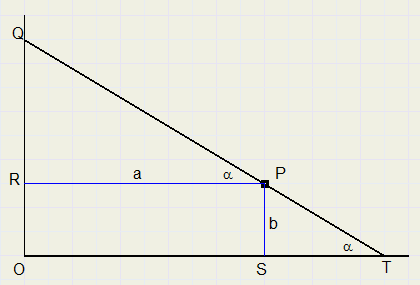
|
| fig.1 |
O is het hoekpunt van een rechte hoek.
Binnen deze hoek ligt een willekeurig punt P.
Een lijn door P snijdt de rechthoekszijden in de punten Q en T.
Gevraagd :
De minimale lengte van QT.
Dit probleem lijkt eenvoudig maar is lastig.
Ik geef twee oplossingen, een algebra´sche en een goniometrische.
De algebra´sche oplossing
De kunst is om het punt Q zodanig op de vertikale lijn te plaatsen dat QT minimaal is.We stellen:
OQ= s
PR = a
PS = b
Wegens gelijkvormigheid van driehoeken PRQ en TSP geldt:
ST : SP = RP : RQ

|
Pythagoras in driehoek TOQ:
QT2 = OQ2 + OT2

|
In de laatste regels is s uit de formule gedeeld.
s= 0 is een minimumwaarde.
De noemer wordt 0 voor s = b....een horizontale lijn.
Voor a = 0 wordt s = b .....klopt
Voor b = 0 wordt s = 0 .....klopt
Voor a = b wordt s = 2b.....correct
Een grafische aanpak zou zijn om de formule voor QT te plotten en het maximum af te lezen.
Dat kan met het grafiekenprogramma GraphicsExplorer kijk [ hier ]
Dit programma gebruikt variabelen x en y en constanten a,b,c
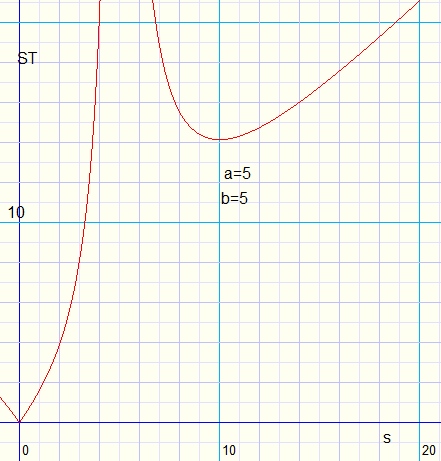
|
Neem y voor QT, x voor OQ en a, b.
Tik : y = sqrt(x2 + ((x*a)/(x-b))2)............{sqrt( ) betekent wortel}
en verander a, b met muiskliks. Lees x af voor het maximum.
In het voorbeeld is a=b=5
ST = 14,4 ...... s = 10
Nog een opmerking:
Het antwoord is een derdemachtswortel.
Daarvoor is geen constructie mogelijk met passer en liniaal.
De goniometrische aanpak
Bekijk weer figuur 1.We stellen een formule op voor QT als functie van α , a en b.
Daarna differentiŰren we QT naar α en stellen de afgeleide 0.

|
Opnieuw vinden we een derdemachtswortel.
Voor de lezer:
Laat zien, dat de resultaten van de algebra´sche- en de goniometrische
oplossing overeenkomen.
De oplossing van Hans Sellmeijer
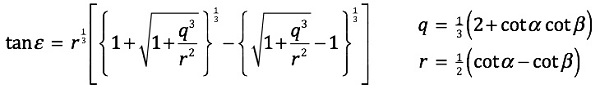
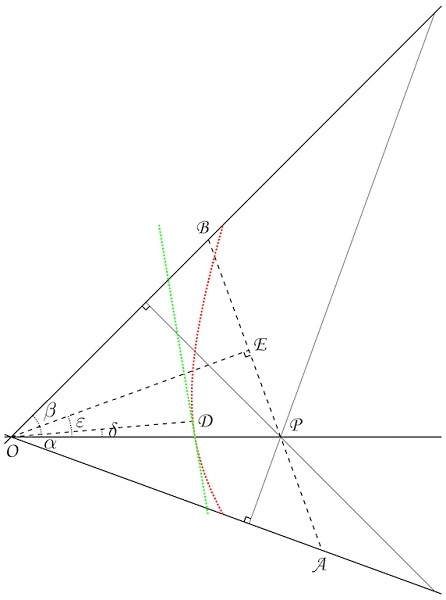
Voor de details is [ HIER ] een pdf bestand.


