meetkunde probleem: De Kortste Zijde.

E.C.Buissant des Amorie / D.E.Dirkse


Let op:
De meetkundige constructie in dit artikel is niet correct.



Zie figuur 1.
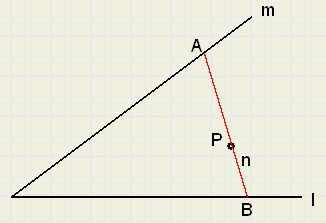
Gegeven zijn de snijdende lijnen l en m en een punt P, dat willekeurig binnen de hoek is gelegen.
Een lijn n door P snijdt l en m in de punten A en B.
Gevraagd :
de constructie van het kleinst mogelijke lijnstuk AB.
    fig.1

Oriëntatie
    fig.2

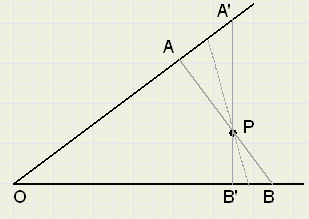
In figuur 2 is AB ^ OA en A'B' ^ OB.
PA is de kortste afstand van P tot lijn OA.
PB' is de kortste afstand van P tot lijn AB.
Het kortste lijnstuk door P zal de benen van hoek AOB ergens tussen
A en A' en tussen B en B' snijden.

Een Analytische aanpak (die niet werkt)
zie figuur 3 hieronder:
    fig.3

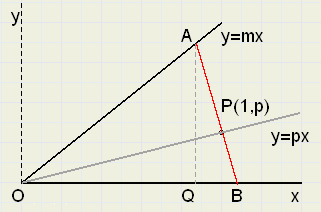
In een coördinatenstelsel geven we OA en OP richtingscoëfficiënten (rc's) m en p.
De x-coördinaat van P geven we waarde 1.
De rc. van AB noemen we s.
De vergelijkingen bij de lijnen zijn dan:
    OA : .......y = mx
    OP:........ y = px
    AB:......... y = s(x - 1) + p
De coördinaten van A en B zijn dan
    xA = 
    p − s
    m − s
     ......... yA = 
    m (p − s)
    m − s
    xB = 
    s − p
    s
Toepassing van Pythagoras in driehoek AQB
    AB2 = yB2 + (xB - xA)2
en na substitutie en wat gereken:
    A B 2 = 
    m 2 (p − s) 2
    s 2 (m − s) 2
     (s 2 + 1)
Gevraagd is dus, bij welke waarde van s AB2 minimaal is,
bij constante waarden van m en p.

Door de afgeleide van AB2 naar s te bepalen en deze nul te stellen,
is de waarde van s (= richting AB) voor een minimale waarde van AB te vinden.
Maar de formule-brij is nietszeggend en de hoeveelheid werk is enorm.
Tijd voor een handiger aanpak, die bovendien aantoont dat toepassing van meetkundige
regels heel veel rekenwerk uitspaart.

Maar eerst twee voorgerechten.

1. Verband tussen Koorde, Hoek en Middellijn in een cirkel
Bekijk figuur 4.
    fig.4

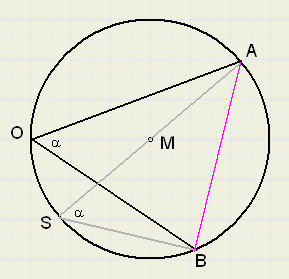
De hoeken bij O en S zijn gelijk, omdat ze beide op cirkelboog AB staan.
Ook is LABS = 90o
(zie artikel : De stelling van Thales)
nu is:
    sin(a) =
    A B
    A S
     ................zodat
    AB = AS.sin(a)
In woorden : een koorde is gelijk aan het product van middellijn en sinus van de hoek op de boog.

conclusie : in bijvoorbeeld fig. 2, zal de kleinste waarde van AB optreden bij de kleinste
omgeschreven cirkel van driehoek AOB.
Ons probleem verandert nu in : zoek de kleinste cirkel door de punten O, A , B.

2. Overweging
Zie figuur 5.
    fig.5

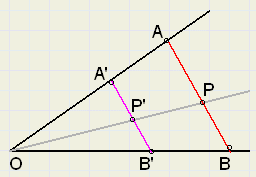
Stel, we vinden in een constructie, dat driehoek A'OB' de kleinste omgeschreven cirkel heeft.
Maar gevraagd wordt de kortste zijde AB, door het punt P.
We verschuiven dan A'B' evenwijdig, zodat deze door P gaat.

De Oplossing
( E.C.Buissant des Amorie )
Zie figuur 6.
    fig.6

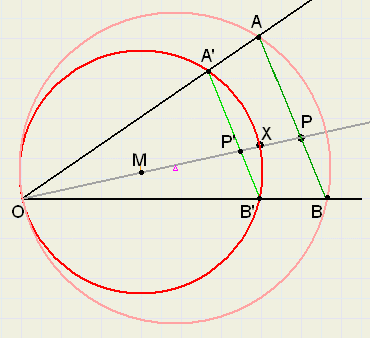
Neem een willekeurig punt X op OP.
Bepaal het midden M van OX.
Teken de cirkel met M als middelpunt en straal OM.
Deze cirkel levert de snijpunten A'en B' op.

AB is de zodanige verschuiving van A'B', dat P op AB ligt.
AB is het gevraagde lijnstuk.

Toelichting
Zie figuur 7.
    fig.7

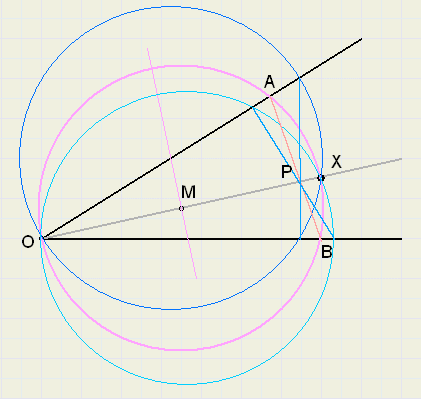
Door O en X is een aantal cirkels getekend.
De middelpunten hiervan zullen liggen op de middelloodlijn van OX.
Voor elke cirkel vinden we een andere AB.
De kleinste cirkel (dus ook AB) heeft M (op OX) als middelpunt.
P is het snijpunt van AB met OX.
Evenwijdige verschuiving naar het echte punt P vergroot de gehele figuur,
maar verandert de eigenschappen niet.

Opmerking: voor elke cirkel in figuur 7. zal een iets verschillend punt P ontstaan.

Berekening van de lengte AB
Zie figuur 6 hiervoor.
Stel gegeven zijn:
    LAOX = a
    LBOX = b
    lengte OP
Hiervan uitgaande, kan AB worden berekend.

Aanpak:
    stel OP' = 1
    bereken dan A'B'
Uit de gelijkvormigheid van de driehoeken A'OB' en AOB volgt dan
    AB : A'B= OP : OP' ..........of
    AB = OP . A'B'
berekening van A'B':
    LOA'X = LOB'X = 90o.....want hoek op middellijn
    L P'A'X = b
    L P'B'X = a ............want hoek op zelfde cirkelboog
    LOA'P' = 90o - b
    LOB'P' = 90o - a
sinusregel in driehoek A'OP'
    A'P' : sin(a) = 1 : sin(90o - b)
    A'P'=
    sin a
    cos b
sinusregel in driehoek B'OP'
    B'P' : sin(b) = 1 : sin(90o - a)
    B'P'=
    sin b
    cos a
Uit .........AB : A'B' = OP : OP' = OP ........volgt
    AB = OP (
    sin a
    cos b
     + 
    sin b
    cos a
    )