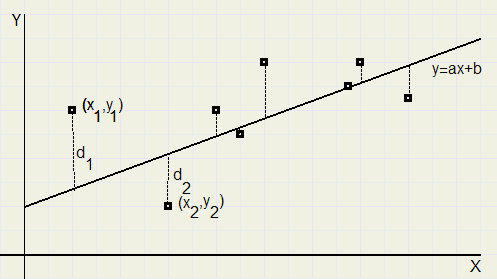
De Kleinste Kwadraten Methode Inleiding Het verband tussen twee rijtjes getallen is aan te geven met een tabel een grafiek een formule Elk tweetal punten van de tabel kan als punt (x,y) in een coördinatenstelsel worden getekend. Daarbij kan dan de best passende formule worden gezocht. Bekijk als voorbeeld het plaatje rechts: getekend zijn de punten (x1,y1)....(x5,y5) en gevraagd wordt de best passende eerstegraads polynoom door deze punten. Onder "best passend" verstaan we die grafiek, waarbij de som van de kwadratische afwijkingen minimaal is. Die afwijkingen zijn rechts gestippeld getekend. De gebruikte "Kleinste Kwadraten Methode", om de best passende polynoom door de punten te vinden, is een fraaie toepassing van de lineaire algebra. Mijn grafieken programma Graphics-Explorer gebruikt de Kleinste Kwadraten Methode om de beste polynoom (graad 0..7) van een verzameling punten te berekenen. de Kleinste kwadraten methode Gegeven zijn de punten (x1,y1) , (x2,y2)...(xn , yn) Gevraagd: een polynoom, graad m, y = c0 + c1x + c2x2 + ... + cmxm door deze punten zodat de afwijking minimaal is. Als de polynoom precies door de punten gaat, dus als m+1 = n, dan geldt: y1 = c0 + c1x1 + c2x12 + ... + cmx1m y2 = c0 + c1x2 + c2x22 + ... + cmx2m ............. ............. yn = c0 + c1xn + c2xn2 + ... + cmxnm geschreven als matrix: ­ y1 ­ y2 ... ... yn = ­ 1 x1 1 x1 2 ... x1 m ­ 1 x2 1 x2 2 ... x2 m .. .. .. .. .. .. .. .. .. .. 1 xn 1 xn 2 ... xn m ­ c0 ­ c1 .. .. cm of korter: y = M . c Als de polynoom niet precies door de punten gaat, dan zal er een verschilvector bestaan: y - M . c De norm van deze verschilvector is de som van de kwadratische afwijkingen. Gezocht wordt dus c , waarvoor || y - M . c || minimaal is. Dat is het geval, als deze verschilvector loodrecht staat op de kolomruimte van M. Het inwendig product is dan gelijk aan nul. (M c )t ( y - M c) = 0 (ct Mt) (y - M c) = 0 ct ( Mt ( y - M c)) = 0 ct ( Mt y - Mt M c ) = 0 zodat: Mt y - Mt M c = 0 Mt M c = Mt y (Mt M)-1Mt M c = (Mt M)-1Mt y c = (Mt M)-1 Mt y Opmerkingen 1. Met Mt wordt bedoeld de matrix M, gespiegeld om zijn hoofddiagonaal. Als M =  ­ 2 0 3 ­ 1 5 8 dan is   M t    =  ­ 2 1 ­ 0 5 3 8 2. rekenregel: ( A B)t = BtAt 3. Het inwendig product van twee vectoren a en b is te schrijven als at.b 4. In het geval van lineaire regressie, dus m = 1 en c =[b,a] .......{immers de lijn heeft de vergelijking y = b + ax..} geldt:   y      =    ­ y1 ­ y2 ... yn   M      =    ­ 1 x1 ­ 1 x2 ... ... 1 xn Mt = ­ 1 1 ... 1 ­ x1 x2 ... xn uitgaande van MtMc = Mty   ­ 1 1 ... 1 ­ x1 x2 ... xn      ·    ­ 1 x1 ­ 1 x2 ... ... 1 xn         ­ b ­ a      =      ­ 1 1 ... 1 ­ x1 x2 ... xn      ·    ­ y1 ­ y2 ... yn ­ n Σ xi ­ Σ xi Σ xi 2  ·  ­ b ­ a  =  ­ Σ yi ­ Σ xi yi ­ b n + a  Σ xi ­ b  Σ xi  + a  Σ xi 2  =  ­ Σ yi ­ Σ xi yi Het volgende stelsel vergelijkingen moet dus worden opgelost: b n + a  Σ xi  =  Σ yi b  Σ xi  + a  Σ xi 2  =  Σ xi yi of Σ xi yi  − a  Σ xi 2  − b  Σ xi  = 0 Σ yi  − a  Σ xi  − b n = 0 of Σ (xi yi − a xi 2 − b xi)  = 0 Σ (yi − a xi − b)  = 0 Voor de oplossing verwijs ik naar mijn artikel Lineaire Regressie Zie formules ....1) en .............2) Voorbeeld Zoek de kleinste kwadraten rechte lijn door de punten (0,1) (1,3) (2,4) en (3,4)   M      =    ­ 1 0 ­ 1 1 1 2 1 3 M t =  ­ 1 1 1 1 ­ 0 1 2 3 M t M =  ­ 4 6 ­ 6 14 (M t M) −1 = 0 , 1  ­ 7 −3 ­ −3 2 c = 0 ,    1  ­ 7 −3 ­ −3 2   ­ 1 1 1 1 ­ 0 1 2 3         ­ 1 ­ 3 4 4    =      ­ 1.5 ­ 1   De gezochte lijn is dus y = 1,5 + x