Differentiaalrekening (1)

naar deel 2
naar deel 3
naar deel 4

Differentiaalrekening is bedacht door de Engelse wis- en natuurkundige Isaac Newton (1643-1727)
en de Duitse wiskundige Gottfried Leibniz (1646-1716).
Eerder werden wel overeenkomstige berekeningen gemaakt, maar Newton en Leibnitz kwamen
als eersten met een algemene theorie.

De differentiaalrekening, ook wel genoemd "hogere wiskunde" was een doorbraak.
Hiermee werd het mogelijk om de oppervlakte van cirkels en de inhoud van bollen te berekenen.
De (zak)rekenmachine gebruikt differentiaalrekening voor de berekening van
de sinus, cosinus of tangens en logaritmen.

Dit is deel 1 van een korte cursus differentiaalrekening.

De basis



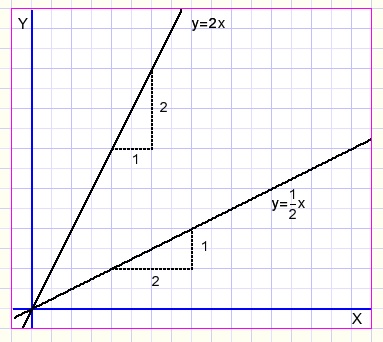
fig1.

Hierboven staat een rechthoekig coördinatenstelsel met twee lineaire functies (y=0,5x en y=2x)
De algemene vergelijking van lijnen door de oorsprong (0,0) is y = ax
a heet hellingsgetal of richtingscoëfficiënt.
De grootte van a bepaalt de steilheid van de lijn.
Voor positieve a loopt de lijn schuin omhoog, bij negatieve a omlaag.
Als x met 1 toeneemt, dan neemt de functiewaarde y toe met a.
a is dus de (absolute) groeisnelheid van de functie.
Bij rechte lijnen is die groeisnelheid voor alle waarden van x gelijk.

Dat is bij gekromde lijnen niet het geval.
Wanneer we een gekromde lijn in een zeer klein gebiedje beschouwen, dan zien we echter
een rechte lijn.
(De aarde is een bol, maar op landelijke schaal kunnen we van een plat vlak uitgaan).
Zolang dus kromme lijnen geen knikken en abrupte sprongen vertonen kunnen we op elk
punt wel degelijk de groeisnelheid bepalen.
Die groeisnelheid is dan het hellingsgetal van het kleine stukje dat we als rechte lijn beschouwen.


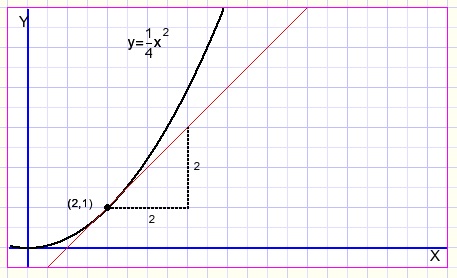
fig2.

Op de parabool y=0,25x2 is in het punt (2,1) de raaklijn getekend.
Die heeft daar een hellingsgetal 1.

Nu gaan we een algemene formule zoeken voor de steilheid van een willekeurige functie f(x).
NB: een functie is een vergelijking die geschreven is in de vorm y = ...x.....
Voor y schrijven we ook wel f(x).
Bij één bepaalde waarde van x is de waarde van y te berekenen.
Die nieuwe functie heet de afgeleide van y {of f(x)} en we noemen die y'...spreek uit y accent,
of f'(x)...spreek uit f accent x.
De functie f'(x) geeft dus voor elke waarde van x de steilheid van f(x).


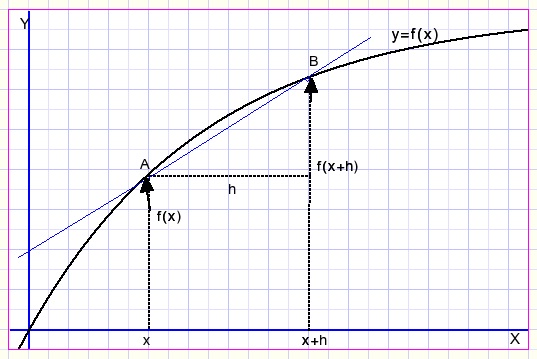
fig3.

Daartoe kiezen we op f(x) twee punten A en B.
B ligt horizontaal over de X-as gemeten een afstandje h van A af.
In punt A is de functiewaarde f(x).
In punt B is de functiewaarde f(x+h).
We trekken een rechte lijn door A en B en van die lijn is het hellinggetal (of richtingcoëfficiënt)


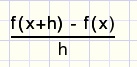
fig4.

Dit is niet erg nauwkeurig.
De getrokken lijn door A en B is geen raaklijn.
Maar daar is wat aan te doen: we bewegen punt B over y=f(x) naar A toe.
Dan zal de rechte lijn naderen tot de raaklijn.
Nu komt de truuk:
    Als B nadert tot A dan nadert de lijn AB de raaklijn aan f(x) in punt A.
    Waar we toe naderen is dus precies wat we zoeken.
De formule van fig.4 noemen we het differentiequotient
Waar we toe naderen als h nadert tot nul heet het differentiaalquotient

De algemene formule voor de afgeleide functie f'(x) luidt:


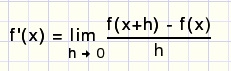
fig5.

De afkorting lim is van limiet, dat is waar we toe naderen als h nadert tot 0.

Voorbeeld
We bepalen de afgeleide functie van y=x2, een simpele parabool.
Opmerking: we kunnen ook schrijven f(x)=x2.


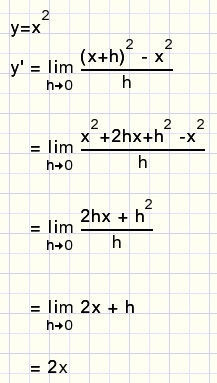
fig6.

Toelichting:
Na wegwerken van de haakjes blijft in de teller over: 2hx + h2.
h nadert tot 0, maar wordt niet 0 zodat we teller en noemer door h mogen delen.
Dan blijft over 2x+h en dat nadert tot 2x als h nadert tot 0.
De afgeleide functie van y = x2 is:
    y'=2x
Hoe groot is de richtingscoëfficient van de raaklijn in punt (5,25) van parabool y=x2?
Simpel: y'= 2x = 2.5 = 10.

De afgeleide van y = xn
Hiervoor is nodig het Binomium van Newton, kijk [HIER].


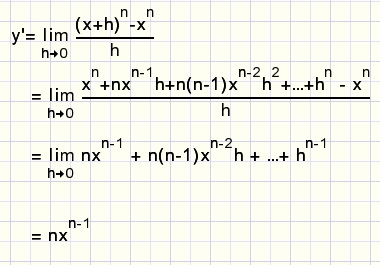
fig7.

Dat is opmerkelijk simpel.
Zet de macht voor de x en verlaag de macht daarna met 1.
De afgeleide functie van y = x10 is dus y'= 10x9.

Notatie

Het is nu tijd om de notatie wat aan te passen.
Hiervoor lieten we x aangroeien met een kleine waarde h.
Maar een veel gebruikte schrijfwijze is Δx inplaats van h.
Bij y = f(x) zal een verandering van x met Δx een verandering van y opleveren en
het is logisch die Δy te noemen.
Δy = f(x+Δx) - f(x)
Zie de figuur hieronder.


fig8.

Als y = ...x..... {een formule met x)
dan is y' de afgeleide functie, we zeggen: y gedifferentieerd naar x
wat ook wordt geschreven als dy/dx.
dy/dx heet het differentiaalquotient.

Toepassing
De oppervlakte A (area) van een cirkel met straal r is A = π r2
r neemt toe met Δr waardoor A toeneemt met een waarde ΔA
Dat extra schilletje rollen we uit, zie de volgende figuur:


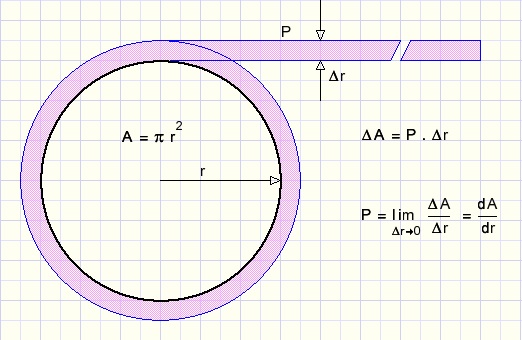
fig9.

De omtrek P (perimeter) van een cirkel verkrijgen we door de oppervlakte naar de straal te differentiëren.
Dus P = 2π r
Hoe we aan A = π r2 komen wordt hier niet behandeld.

Regels voor de afgeleiden van functies


1a.De constante functie
y = c
y'= 0

1b.De lineaire functie
y = ax + b
y'= a

Opmerking: x0 = 1

Voorbeeld:
Als y = 23 dan is y'= 0. De functie heeft altijd de waarde 23, er is geen verandering.

2.Vermenigvuldigen met een constante.
y = c.f(x)
y'= c.f'(x)

Voorbeeld:
Als y = 3x2 dan is y'= 2.3x = 6x.

Om hierna niet in omvangrijk schrijfwerk te vervallen voeren we nog wat notatie in.
Stel u = f(x) en v = g(x), u en v zijn beide functies van x.
Bijvoorbeeld: u = 3x+2 en v = 5x2 -4x + 11, ik schrijf zo maar wat op.

Dan kunnen we u en v differentieëren naar x, wat u' en v' oplevert, de afgeleide functies.
Neem x toe met Δx dan neemt u toe met Δu en v met Δv.

3.De som van functies
y = u + v
y'= u' + v'

bewijs:


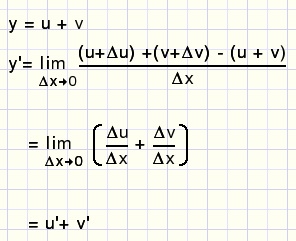
fig10.

Voorbeeld:
y = x3 + x2 + x + 1
y'= 3x2 + 2x + 1

4.Het product van functies.
y = uv
y'= uv' + vu'

Bewijs:


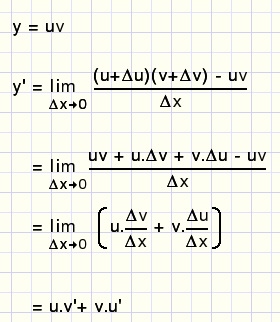
fig11.

Voorbeeld:
y = x2.(x3 + 6x)
y'= x2.(3x2 + 6) + 2x.(x3 + 6x) = 5x4 + 18x2.

We hadden ook kunnen berekenen:
y = x5+ 6x3

5.Het quotient van functies.
Zie figuur:


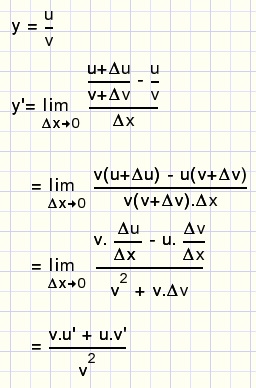
fig12.

In woorden: (noemer*afgeleide teller - teller*afgeleide noemer) gedeeld door de noemer in het kwadraat.

Voorbeeld (1): y = x3 / x2
y' = 1.
De berekeningen laat ik aan de lezer over.

Voorbeeld (2):
y = 1/x
y'= (x.0 - 1.1)/x2 = -1/x2

Negatieve machten.
y = xn
y'= nxn-1
maar geldt dat ook voor negatieve waarden van n, dus als de macht in de noemer staat?

Laat n een geheel positief getal zijn.
We nemen y = x-n.xn. Dat betekent dat y = 1 zodat y'= 0
De afgeleide van x-n noemen we even Z.
Toepassing van de productregel:
y'= Z.xn + x-n.n.xn-1 = 0
Z.xn = -n.x-1
Z = -n.x-n-1
waaruit blijkt dat de regel ook geldt voor negatieve machten.

Toepassingen

De differentiaalrekening maakt het mogelijk op simpele wijze de extreme waarde (minimum of maximum) van een functie te bepalen.
In die punten is namelijk de afgeleide = 0, de raaklijn aan de functie loopt daar horizontaal.
We bepalen de extreme waarde van y = 0,2x2 - 1,6x + 4,2.
differentiëren: y'= 0,4x - 1,6 = 0
x = 4, dus y = 0,2.42 - 1,6.4 + 4,2 = 1.
Op punt(2,1) treedt een extreme waarde op.
Dat moet een minimum zijn, want we hebben hier een dalparabool.


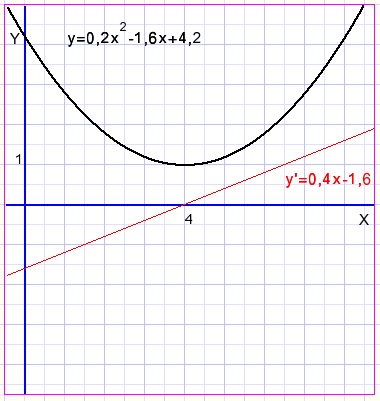
fig13.

De afgeleide functie is in rood getekend.
Voor x=4 heeft y' de waarde nul.
Voor x < 4 is y' negatief, voor x > 4 positief.
Aan het teken van de afgeleide van de afgeleide oftewel y'' (y dubbel accent)
is dus te zien of er een minimum of maximum optreedt.
Links van x=4 daalt de functie, de richtingscoëfficiënt (rc) is negatief.
Daarna stijgt de functie, dus de rc is positief. y'' = 0,4 > 0 dus minimum.

Nog een voorbeeld.
We zoeken de extreme waarden van de functie y = (1/3)x3 - 3.5x2 + 10x -8


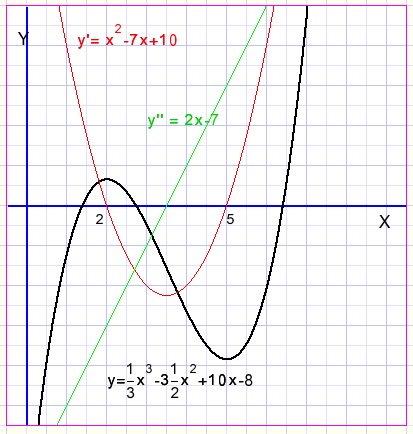
fig14.

Differentiëren:
y'= x2 - 7x + 10.
De afgeleide 0 stellen:
x2 - 7x + 10 = 0 ....ontbinden in factoren (of ABC formule gebruiken)
(x-2)(x-5) = 0
x = 2 ...of.... x = 5.

y''= 2x-7.
Voor x=2 geldt: y''= -3 < 0 ......dus maximum
Voor x=5 geldt: y''= 3 > 0 ...... dus minimum

Voor y''=0 treedt een buigpunt op, een toenemende daling gaat bij x=3,5
over in een afnemende daling.

Samenvattend:
    - voor een maximum of minimum van een kromme geldt: y'= 0.....(raaklijn loopt horizontaal)
    - voor een minimum geldt : y'' > 0
    - voor een maximum geldt : y'' < 0
    - voor y''= 0 treedt een buigpunt op, toenemende stijging of daling gaat over in afnemende stijging of daling

Mechanica

Gemiddelde snelheid is afstand / tijd.
De snelheid op een bepaald tijdstip is het differentiaalquotient van afstand en tijd,
dus afstand gedifferentieerd naar tijd.
Versnelling is dan weer de snelheid gedifferentieerd naar de tijd.
Voor een valbeweging geldt dat de afgelegde weg S = 0,5.gt2
waarbij g = 9,8m/sec2, de zwaartekrachtsversnelling.
De snelheid V van een vallend voorwerp is na t seconden: V = gt
We zien, dat V = dS/dt.
Door V naar t te differentiëren rolt de versnelling g eruit.

Nu slingeren we een gewicht rond aan een touw en vragen ons af
welke kracht het touw moet uitoefenen om het gewicht in een cirkelvormige baan te houden.

Neem m als massa (kg) van het ronddraaiende voorwerp.
De straal van de cirkel is r.
De snelheid van het voorwerp is v (m/sec).
Per seconde wordt dus de cirkel v/(2 π r) maal rondgegaan.
Rekenen we de doorlopen hoek in radialen (3600 = 2π radialen) dan wordt
elke seconde dus een hoek afgelegd van v/r radialen.


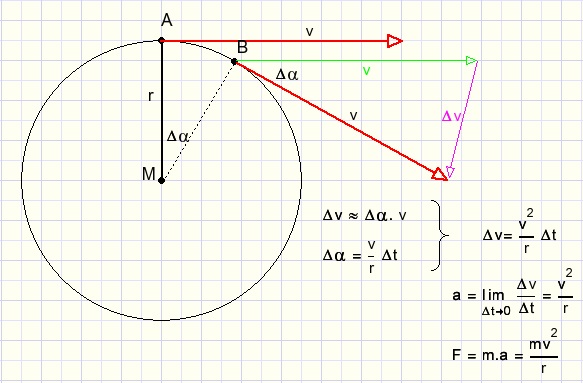
fig15.
a is de versnelling die massa m moet ondergaan om niet rechtdoor te vliegen.
NB: Bij een middelpuntshoek van α radialen hoort een cirkelboog met lengte a.r.

Als we een steen van 3kg. rondslingeren aan een touw van 3 meter lang en elke seconde rond gaan,
dan is v = 18,85m/sec en we moeten een kracht uitoefenen van F = 355Newton, dus zo'n 36 kg.

Gedachte

Stel G is de toestand op onze planeet en t is de tijd.
Dan geldt: nieuws = dG / dt, het differentiaalquotient van de toestand en de tijd.
Explosies en ongevallen zijn groot nieuws omdat zij zich in zeer korte tijd voltrekken.

Hiermee besluit ik deel 1 van deze snelcursus differentiaalrekening.