

| Van Knikkerplank tot het Binomium van Newton |  |
Hieronder is een knikkerplank getekend:
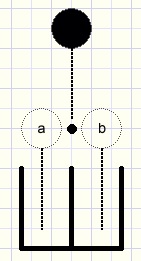
fig1.
De knikker valt omlaag op een spijkertje en kan dat links of rechts passeren.
De keuze van de linkerkant noemen we a en de rechterkant b.
Daarna valt de knikker verder in het bakje eronder.
De plank breiden we uit met twee spijkertjes en een bakje:
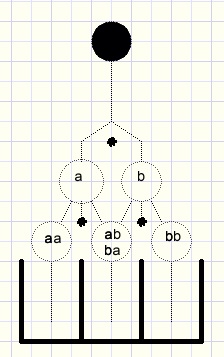
fig2.
De knikker valt in het meest linkse bakje als de keuze twee keer a (links) is.
Het pad van de knikker noemen we aa.
Het pad voor het meest rechtse bakje is bb.
De paden ab (eerst links dan rechts) en ook ba (eerst rechts dan links)
brengen de knikker in het middelste bakje.
Het gevolg van handeling a gevolgd door handeling b schrijven als het product ab.
De keuze van de knikker bij botsing met een spijkertje noemen we a+b lees: a of b.
Het linker bakje kunnen we a2 noemen, het middelste ab + ba en het rechter b2
Omdat hier geldt dat ab = ba is het middelste bakje ook 2ab te noemen.
Fig1. met 1 spijkertje: (a + b)1 = a + b
Fig2. : de knikker passeert twee spijkertjes.
Twee keer moet de keuze a+b worden gemaakt dus de mogelijke paden worden:
(a + b)(a + b) = (a + b)2 = aa + ab + ba + bb = a2 + 2ab + b2.
Nog een rij spijkertjes en een bakje erbij:
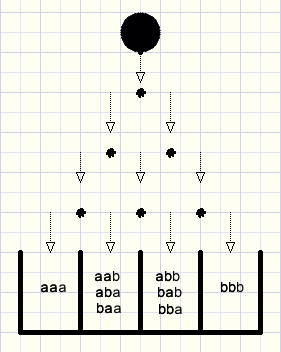
fig3.
Nu moet de knikker 3 maal achtereen de keuze a+b maken.
(a + b)(a + b)(a + b) = (a + b)3 = aaa + aab + aba + baa + abb + bab + bba + bbb = a3 + 3a2b + 3ab2 + b3
a3 + 3a2b + 3ab2 + b3 is ook te schrijven als:
1.a3 + 3.a2b + 3.ab2 + 1.b3
(de punt. staat voor vermenigvuldigen)
Er is 1 pad naar het bakje a3.
Naar de bakjes a2b en ab2 lopen elk 3 paden en
naar bakje b3 is er weer 1 pad.
In de formule 1.a3 + 3.a2b + 3.ab2 + 1.b3
heten de getallen 1, 3, 3 en 1 de coŽfficiŽnten van de termen a3, a2b, ab2 en b3.
Een gokspel.
Stel eens dat we op de markt staan met een knikkerspel als in fig3.
Een bezoeker betaalt 1 euro om een knikker te laten rollen.
Komt de knikker in het linker of rechter bakje dan betalen we 3 euro uit.
Zal dit ons winst of verlies opleveren?
De knikker moet drie keer een a of b keuze maken, dus zijn er 2 * 2 * 2 = 8 paden,
evenveel als 1 + 3 + 3 + 1 de som van de coŽfficienten.
Naar het linkse en rechtse bakje lopen 1 + 1 = 2 van de 8 wegen.
De kans dat de knikker daar terechtkomt is 2/8 = 25%.
In 25% van de gevallen moeten we 3 euro uitbetalen.
1 - 0,25*3 = 25 cent, onze gemiddelde winst per spel.
Daarbij nemen we aan dat de knikkerplank eerlijk is geconstrueerd.
Bovenstaande voorbeelden zijn uit te breiden met steeds meer spijkertjes en bakjes.
Het bepalen van de coŽfficiŽnten wordt dan een steeds lastiger klus.
Is er geen simpeler methode?
De Franse wiskundige Pascal (1623 - 1662) bedacht daar wat op.
Hieronder staat de zg. driehoek van Pascal waarin elk getal de som is van de twee getallen er links- of rechts boven.
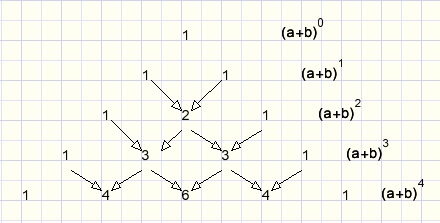
fig4.
Hier is meteen af te lezen dat
(a+b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4.
Elke term bevat 4 factoren, de a en b in alle mogelijke combinaties.
Deze driehoek was al eeuwen eerder bij de Chinezen bekend.
Maar bij hogere machten wordt ook de driehoek van Pascal nog wel bewerkelijk.
Zou er geen formule te vinden zijn om de coŽfficiŽnten te berekenen?
Dat vroeg de Engelse wis- en natuurkundige Newton (1643 - 1727) zich ook af en
hij slaagde erin die formule te vinden.
Het binomium van Newton
Bekijk opnieuw figuur 3.
Er zijn 3 wegen naar bakje a2b namelijk aab, aba, baa.
Evenveel wegen als 2 letters a en 1 letter b op een rijtje zijn te zetten.
De 5 letters a,b,c,d,e zijn op 5*4*3*2*1 manieren op een rijtje te zetten want:
- voor de eerste letter zijn er 5 keuzes
- voor elke volgende letter is er steeds een keuze minder.
Het product 5*4*3*2*1 schrijven we korter als 5! ...spreek uit 5 faculteit.
5! = 120
6! = 720
Vijf letters a zijn op maar 1 manier op een rij te zetten.
Maar als we ze ongelijk maken dan zijn er opeens 5! = 120 rijtjes mogelijk.
Bij 5 gelijke letters moet dus het aantal rijtjes door 5! worden gedeeld,
het aantal gevallen waarin de rangschikking geen verschil maakt.
Neem nu het middelste vakje in figuur 4: 6.a2b2
Het aantal rijtjes met de letters aabb is 6 (aabb,abab,abba,baab,baba,bbaa)
Bij 4 verschillende letters zouden er 4! rijtjes zijn, maar omdat er twee a's zijn moet door 2!
worden gedeeld en omdat er ook twee b's zijn moet opnieuw door 2! worden gedeeld.
Nu een moeilijker voorbeeld:
We gaan uit van (a+b)10 = a10 + ....+ 120a7b3+ ...+ b10
De coŽfficiŽnt 120 ontstaat zo:
- er zijn samen 10 a's en b's, die zouden indien verschillend 10! rijtjes kunnen maken
- er zijn 7 gelijke a's, dus 10! delen door 7!
- er zijn 3 gelijke b's, dus delen door 3!
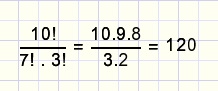
fig5.
Omdat dit soort berekeningen veel voorkomen is er een kortere notatie voor bedacht:
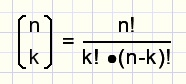
fig6.
Spreek uit: n boven k (geen breukstreep zetten)
In figuur 5. is: n=10 en k=7
Symmetrie: n=10 en k=(10-7) geeft het zelfde antwoord.
Afspraak: 0! = 1
Rekenregel:
-
(p+1)p! = (p+1)!
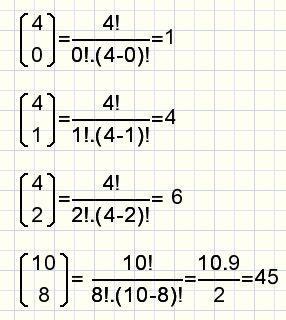
fig7.
Met deze n boven k notatie kunnen we de coŽfficiŽnten mooi in de Pascal driehoek zetten:
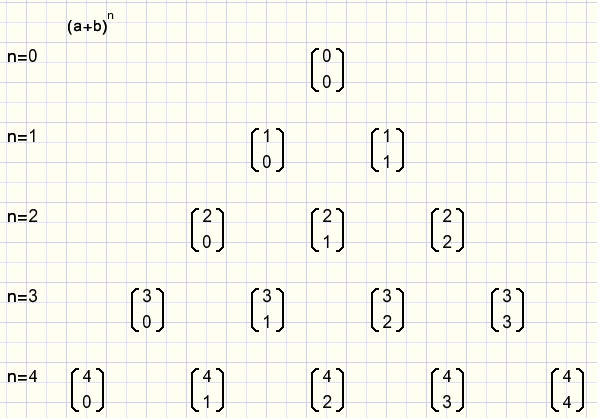
fig8.
We kunnen nu bijvoorbeeld direct opschrijven:

fig9.
Maar het kan nog een stapje compacter met de som notatie.
Daarbij wordt het Griekse SIGMA teken gebruikt om een rij + tekentjes te vervangen.
Hieronder staan wat voorbeelden van somnotaties:
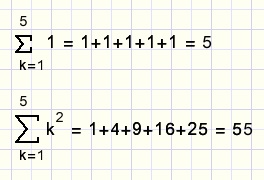
fig10.
k heet de index.
Onder het somteken staat de beginwaarde van de index.
De eindwaarde staat erboven.
En dan komen we tenslotte aan bij het binomium van Newton
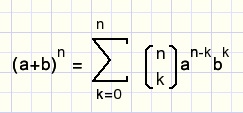
fig11.
Toevoeging
Bekijk nog eens figuur 8.
Kijk horizontaal en ook diagonaal van links boven naar rechts onder.
Dan zien we dat moet gelden in het algemene geval:
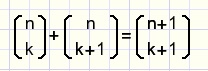
fig12.
Dit staat bekend als de optel regel.
Het bewijs leveren we door elke term te herschrijven als een coŽfficiŽnt gevolgd door n boven k
en die daarna uit elke term te delen.
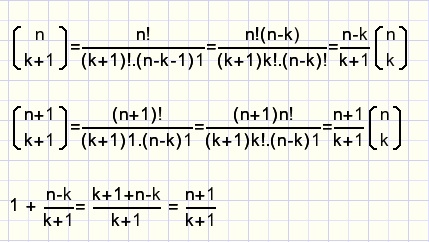
fig13.
Het klopt ook nog.
Vraagje
Waarom is:
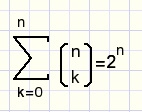
fig14.
Hint: welke waarden van a en b worden hier aangenomen?
Het Binomium van Newton vindt veel toepassing in de wiskunde.
Newton zelf had het nodig voor zijn differentiaalrekening om de afgeleide functie van xn te vinden.
Maar ook in de combinatoriek en kansrekening komen we het binomium tegen.
Voorbeeld
We zijn met een reisgezelschap van 25 personen op weg door een tropisch land.
Bekend is dat elke persoon 10% kans heeft een ziekte op te lopen.
De kans dat niemand ziek wordt is dus 0,925 = 7,2%
Hoe groot is de kans dat er precies 5 personen ziek worden?
Dit lijkt op het knikkerplanken probleem waarbij a = 0,9 (niet ziek) en b = 0,1 (wel ziek).
Met 25 x die keuze ontstaat voor 5 zieken (k=5):

fig15.
NB: bij het knikkerplankenprobleem kunnen we ook stellen:
a = 1/2 en b=1/2, de kans op links- of rechtsom.
Elke term van het binomium is dan de kans dat de knikker in het betreffende bakje belandt.

