Cursus Differentiaalrekening (2)

naar deel 1
naar deel 3
naar deel 4

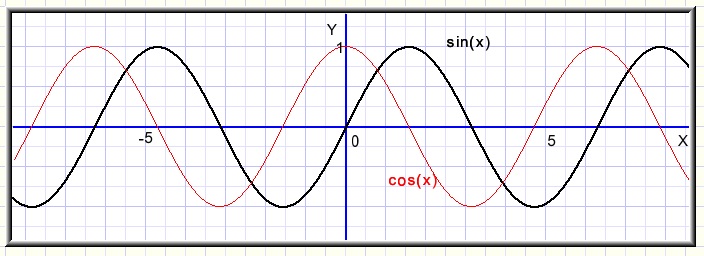
De afgeleide van sin(x)


Opmerking: de hoek x wordt gerekend in radialen.
3600 = 2π radialen.



y = sin(x)
y'= cos(x)

Vooraf:

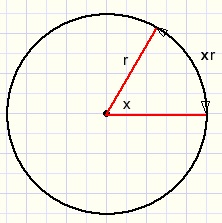
Een middelpuntshoek van x radialen staat op een cirkelboog van lengte xr.
(r is de straal van de cirkel)
want: de hele omtrek = 2πr, bij 1 radiaal hoort een cirkelboog met lengte r.



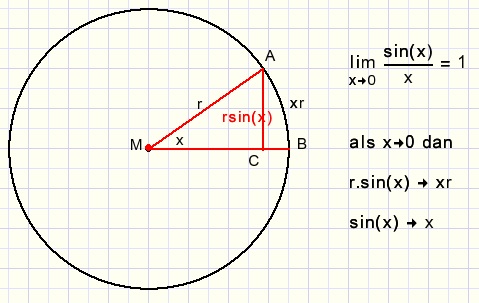
Voor het bewijs hebben we de volgende limiet nodig:
(waaruit blijkt hoe handig het is hoeken in radialen te meten)



Bewijs:



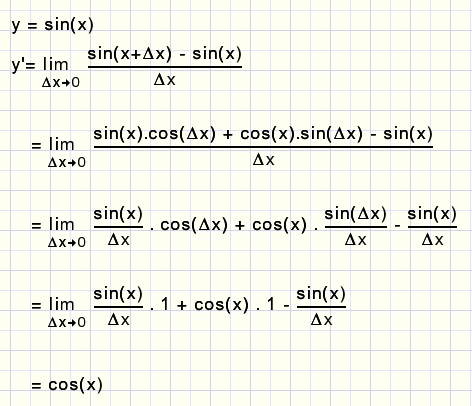
De afgeleide van cos(x)




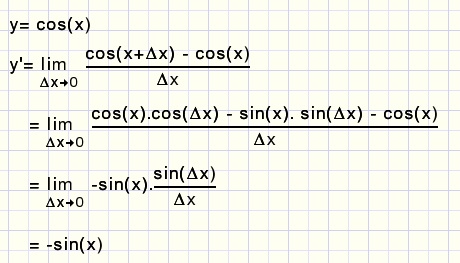
De afgeleide van tan(x)

Stel u = sin(x) en v = cos(x) en pas de quotientregel toe (zie deel 1)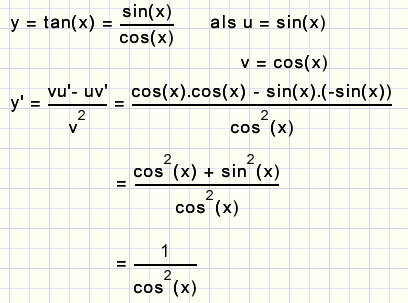



De Kettingregel

Een functie levert altijd 1 getal op.
Functies kunnen daarom in formules de plaats van getallen innemen.
Stel y = sin(x3)
Voor het differentiëren hiervan hebben we nog geen recept.
Een wiskundige knipt het probleem dan in stukjes die wel bekend zijn.
Stel eens: u = x3, we kunnen dan u naar x differentiëren: u' = 3x2.
In y = sin(u) kunnen we ook y naar u differentiëren, dat levert cos(u).
Het hele probleem wordt oplosbaar door de afgeleiden te schrijven als differentiaalquotient:



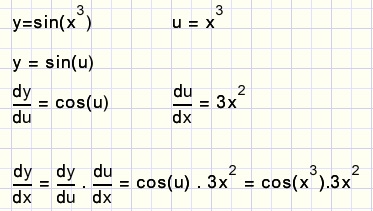
Opmerking: dy,dx,du: dat zijn getallen waarmee we gewoon kunnen rekenen.

De kettingregel kan eindeloos worden uitgebreid met steeds weer functies binnen functies.
Neem bijvoorbeeld y = sin3(x2-5x+7).



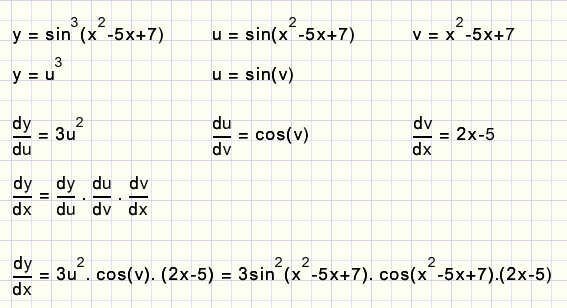
Differentiëren van gebroken machten

We zoeken de afgeleide functie van y=x0,5 oftewel de wortel uit x.
Mogen we daar de regel voor y = xn voor gebruiken?
Met de kettingregel kunnen we dat ontdekken.

We gaan uit van y = (x0,5)2.....dus eigenlijk y = x.



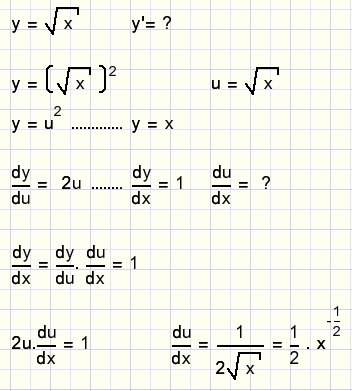
Met de regel voor y = xn........y'= nxn-1 vinden we hetzelfde antwoord.
Deze regel geldt ook voor gebroken machten.

Hieronder staat het algemene bewijs:



Voorbeelden:



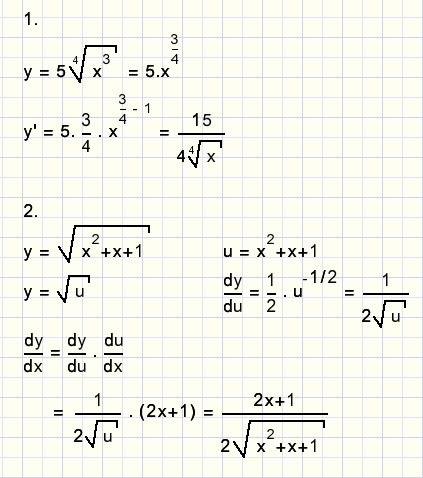
f(x) = f '(x) ?

Zou er een functie bestaan die zijn eigen afgeleide is?
Dus waarvan de functiewaarde op elk moment gelijk is aan de richtingscoëfficiënt?
Laten we eens op zoek gaan.

Voor zo'n functie moet het volgende gelden:



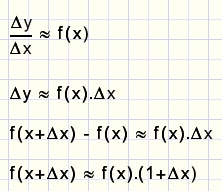
Wat we zien:
Als x met een klein stapje Δx toeneemt, dan moet f(x) met (1+Δx) worden vermenigvuldigd.
Laten we het interval [0..1] van x eens beschouwen.
We knippen dat interval op in n gelijke stukjes waarbij n.Δx = 1.
Gaande van 0 naar 1 is de functiewaarde dus n maal vermenigvuldigd met (1+Δx).
Als a =f(0), dan is f(1) = a.(1+Δx)n...{a is een constante}



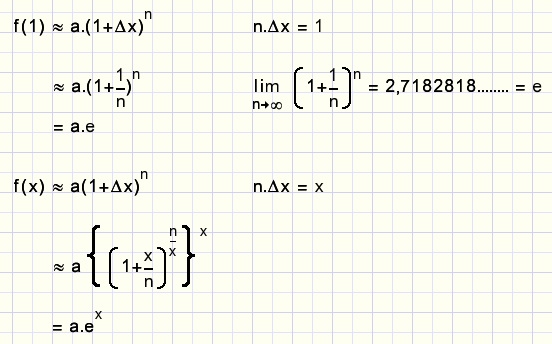
Zie ook: algebra-5
e is het grondtal van de natuurlijke logaritme ln( )

Als y = ex dan y' = ex
Ook mag nog met een constante worden vermenigvuldigd.
Als y = aex
dan y'= aex.

De afgeleide functie van y = ln(x)




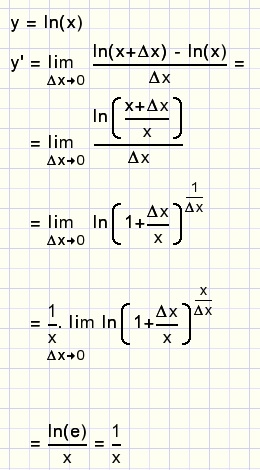
De afgeleide functie van y = ax


Stel ax = epx zodat
ln(ax) = ln(epx)
x.ln(a) = px
p = ln(a)

y = epx
y'= p.epx = ax.ln(a).

De afgeleide functie van y = log(x)




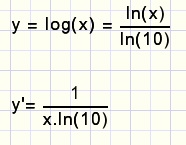
De ln( ) truuk


Hoe differentieer je y = xx?
Stel z = ln(f(x)) dan:



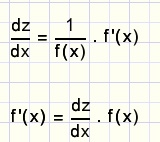
In woorden: in plaats van de functie differentiëren we de ln( ) ervan
en daarna vermenigvuldigen we met de functie.



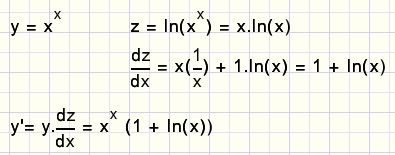
Nog een voorbeeld:



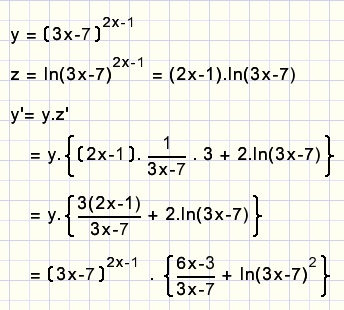
Differentiëren van impliciete functies


Een cirkel met middelpunt (0,0) en straal 6 wordt beschreven door de vergelijking
    x2 + y2 = 36
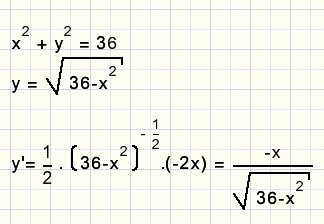
Voor de bovenste halve cirkelboog kunnen we de functie afleiden:



Maar dat resultaat kunnen we ook bereiken met zg. "impliciet" differentiëren
    x2 + y2 = 36
    2x + 2y.y'= 0
    y'= -x/y......voor y de functie uit de vorige figuur invullen.

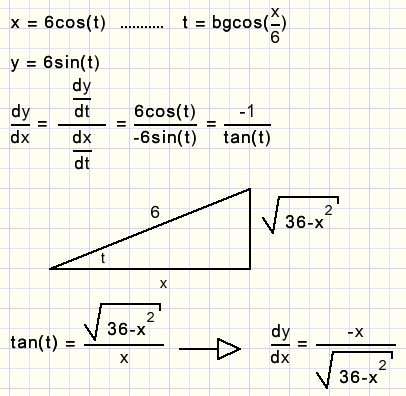
Differentiëren van parameter functies

De cirkel kan ook beschreven worden met een zg. parameter functie.
x en y zijn daarin beide een functie van variable t (de doorlopen hoek):
    x = 6cos(t)
    y = 6sin(t)


Samenvatting van Afgeleiden en Rekenregels




Hiermee besluit ik deel 2 van deze korte cursus differentiëren.