een mysterieuze zeshoek

Inleiding
In figuur 1 hieronder is een driehoek getekend.
Elke zijde is verdeeld in drie gelijke delen.
Vanuit elk hoekpunt zijn lijnen getrokken naar de punten op de tegenoverliggende zijde.
Zo ontstaat in het midden een zeshoek.
In dit artikel bepalen we de verhouding tussen de oppervlaktes van de zeshoek en de driehoek.
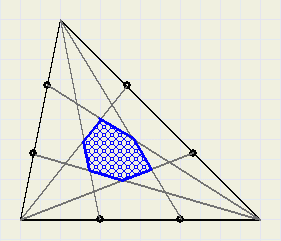    fig.1
Dr. D.J.Smeenk paste de statica (krachten en hefbomen) toe
om het zeshoek probleem op te lossen.
Klik hier voor een artikel over zijn originele aanpak.

Mijn oplossing
Stel de oppervlakte van de gehele driehoek op 1.
Bekijk figuur 2 :
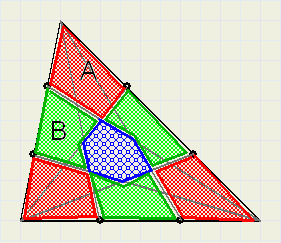    fig.2
daarin zijn twee soorten figuren te onderscheiden:
- de rode, met oppervlakte A
- de groene, met oppervlakte B.

Uit berekening zal blijken:
    oppervlakte A = 1/6
    oppervlakte B = 2/15
Voor de oppervlakte van de zeshoek blijft dan over 1/10, zodat
de zeshoek een tiende deel is van de oppervlakte van de driehoek.

Oppervlakte A
Zie figuur 3. De oppervlakte van een kleine driehoek is met een kleine letter a,b,c,d aangegeven.
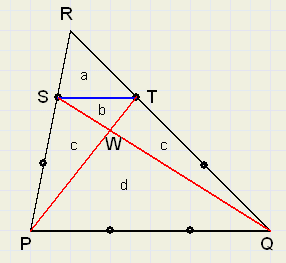    fig.3
Driehoeken PQR en STR zijn gelijkvormig.
    PQ = 3ST, zodat
    a = 1/9
Opmerking:
Als twee driehoeken gelijkvormig zijn, dan verhouden hun oppervlakten zich als de
kwadraten van twee overeenkomstige zijden.

Nu is
    a + b + c = 1/3, zodat
    b + c = 2/9
Opmerking:
beschouw driehoeken QRP met basis QR en TRP met basis TR.
QR = 3TR.
De driehoeken hebben gelijke hoogten.

Ook geldt:
    c + d = 2/3 en
    d = 9b
Opmerking:
Driehoeken TSW en PQW zijn gelijkvormig en PQ = 3ST

Combinerend:
    9b + c = 2/3
    b + c = 2/9 ...........{zie boven}

    b = 1/18
En waar het om ging:
    A = a + b = 1/6

Oppervlakte B
Eerst wordt de oppervlakte e + f berekend.
Zie figuur 4.
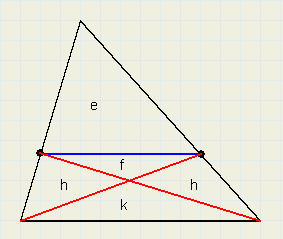    fig.4
    f / k = 4/9 ....{gelijkvormigheid, factor 2/3} zodat
    9f = 4k
    ook is
    h + k = 1/3 zodat
    4h + 4k = 4/3 ...............{4k vervangen door 9f}
    9f + 4h = 4/3

    e + f + h = 2/3
    e = 4/9 ............{gelijkvormigheid met grote driehoek} zodat
    f + h = 2/3 - 4/9 = 2/9 en
    9f + 9h = 2
    9f + 4h = 4/3 ...............{zie hiervoor} dus
    5h = 2/3
    h = 2/15
    e + f = 2/3 - 2/15 = 8/15
Nu kan oppervlakte B worden bepaald, zie figuur 5:
    fig.5
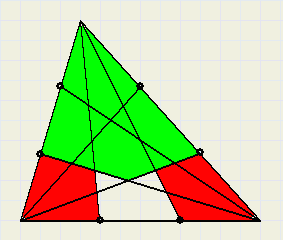
    B = 1 - 8/15 - 2* 1/6 = 2/15
Het resultaat
    oppervlakte zeshoek = 1 - 3 (1/6 + 2/15) = 1/10