Meetkunde met Hefbomen

Dit artikel is geschreven naar een idee van Dr. D.J.Smeenk te Zaltbommel
om de regels van de statica (hefbomen en krachten) toe te passen op meetkundige problemen.
Na een toelichting en enkele voorbeelden, wordt het zeshoek probleem op deze
nieuwe manier aangepakt.

Hefbomen en Evenwicht
Zie figuur 1.
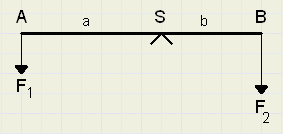    fig.1
Hefboom AB heeft S als steunpunt.
Als in A een kracht F1 omlaag werkt in B een kracht F2, dan geldt bij evenwicht:
    F1.a = F2.b
Anders geschreven:
    a : b = F2 : F1
Als de krachten F2 en F1 bekend zijn, dan kan de verhouding a : b worden berekend.
Als deze verhouding bekend is en de kracht in één uiteinde, dan is de tweede kracht in het tweede uiteinde
te berekenen.
Het steunpunt S draagt de som van beide krachten, F2 + F1.

Deze regel blijft geldig, ook als de hefboom verdraait.
Zolang de krachten maar in dezelfde richting werken.
Bekijk figuur 2.
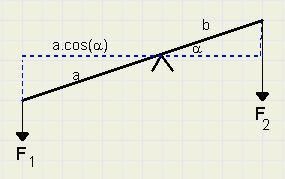    fig.2
Er geldt bij evenwicht:
    F1a.cos(a) = F2b.cos(a)
zodat ook:
    a : b = F2 : F1
Een eerste toepassing
Een stelling in de meetkunde luidt:
    De zwaartelijnen van een driehoek gaan door één punt en verdelen elkaar in de verhouding 2 : 1
    gerekend vanuit een hoekpunt.
Zie figuur 3.
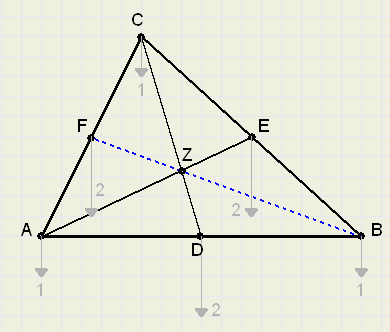    fig.3
De gehele figuur is te beschouwen als een stelsel van verschillende hefbomen en steunpunten.
D is het midden van AB, E is het midden van BC.

Hefboom AB heeft als steunpunt D.
Laat in A een kracht met grootte 1 werken.
Wegens AD = DB, zal in B een even grote kracht werken.
In D werkt dus een kracht 1 + 1 = 2

Hefboom BC heeft als steunpunt E.
Als een kracht 1 werkt in B, dan zal wegens BE = EC ook in C een kracht 1 werken.
In E werkt een kracht 1 + 1 = 2.

Stel dat Z het steunpunt is van hefboom AE.
Dan geldt:
    1.AZ = 2.ZE
zodat
    AZ : ZE = 2 : 1
Enzovoorts.

Een tweede toepassing
Zie figuur 4.
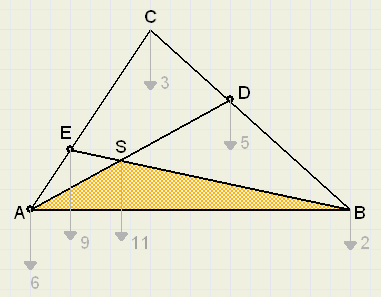    fig.4
Op zijde BC van driehoek ABC wordt punt D zo gekozen, dat BD : CD = 3 : 2
Op zijde AC wordt E gekozen met AE : CE = 1 : 2

Als de oppervlakte van een veelhoek ABCD... genoteerd wordt als [ABCD..]
dan vragen we ons af de verhouding
    [ABS] : [ABC]
oftewel, welk deel is driehoek ABS van driehoek ABC.

We beginnen met in A een kracht aan te nemen van 6.
(handige keuze om breuken te vermijden, maar elke waarde ongelijk 0 zou goed zijn)
Hefboom AC:
    Fc : 6 = 1 : 2
    Fc = 3
    Fe = 6 + 3 = 9
Hefboom BC:
    Fb : Fc = 2 : 3
    Fb = 2
    Fd = 3 + 2 = 5
Hefboom AD:
    AS : DS = 5 : 6
    dus
    AS : AD = 5 : 11
Hefboom BE:
    BS : ES = 9 : 2
    dus
    BS : BE = 9 : 11
Uit bovenstaande volgt:
    [ABD] : [ABC] = BD : BC = 3 : 5
    [ABD] =
    3
    5
     .[ABC]
    [ABS] : [ABD] = AS : AD = 5 : 11
    [ABS] =
    5
    11
     .[ABD] =
    3
    5
     · 
    5
    11
     .[ABC] =
    3
    11
     .[ABC]
Merk op:
zowel voor hefboom AD als hefboom BE wordt in S eenzelfde kracht 11 berekend.

Toelichting (zie fig. 5)
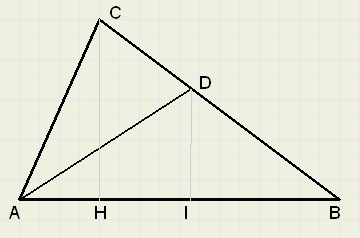    fig.5
Driehoeken ABC en ABD hebben basis AB gemeenschappelijk.
Hun hoogten zijn CH en DI zodat:
    [ABD] : [ABC] = DI : CH
Wegens gelijkvormigheid van DHBC en DIBD :
    DI : CH = BD : BC
zodat
    [ABD] : [ABC] = BD : BC

Een (eerste) hulpstelling
Zie figuur 6:
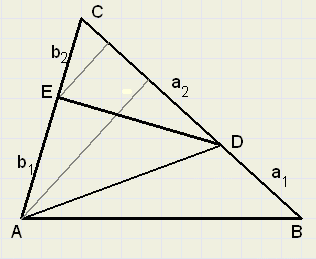    fig.6
Gegeven:
BD : CD = a1 : a2
AE : CE = b1 : b2

Gevraagd:
de verhouding [EDC] : [ABC]

Oplossing:
Beschouw als basis de lijnstukken BC en DC.
    DC : BC = a2 : (a1 + a2)
Voor de hoogten h1 en h2 geldt:
    h1 : h2 = b2 : (b1 + b2)
zodat
    [ECD] =
    a2 b2
    (a1 + a2) (b1 + b2)
     [ABC]
Deze stelling luidt ook wel:
    Als twee driehoeken een hoek gelijk hebben, dan verhouden hun oppervlakten zich
    als het product van hun zijden om die hoek.
Het zeshoek probleem
Zie ook: HIER

Bekijk figuur 7:
D en E verdelen AB in drie gelijke delen.
F en G verdelen BC en H en I verdelen AC in drie gelijke delen.
Vraag : welk deel [PQRSTU] is van [ABC].
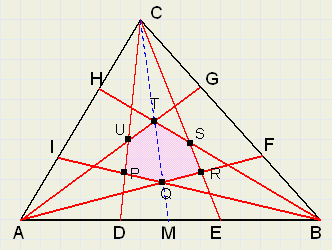    fig.7
Om [PQRSTU] te berekenen, nemen we eerst de helft, dat is [PQTU].
[PQTU] is een deel van [DMC].
Er geldt : [PQTU] = [PQC] - [UTC]

Er moet dus berekend worden welk deel [PQC] en [UTC] zijn van [DMC]
Als laatste moet dan nog de verhouding [DMC] : [ABC] bepaald worden.

Voor het bovenstaande is nodig de (relatieve) posities van U en P op DC en
van Q en T op CM te berekenen.
Daarvoor is de hefboommethode erg geschikt.
De berekening zal voor elk punt op overeenkomstige wijze verlopen.
Om overbodig werk te vermijden kan dus beter eerst een algemene formule
worden afgeleid voor de positie van de punten P,Q,T,U.

Nog een (tweede) hulpstelling
Zie figuur 8.
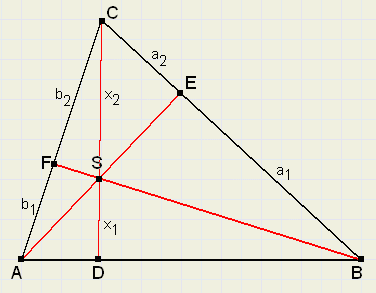    fig.8
E verdeelt BC in de verhouding a1 : a2
F verdeelt AC in de verhouding b1 : b2
Het verlengde van CS snijdt AB in D.

Gevraagd: de verhouding x2 : (x1 + x2)

Berekening:
Beschouw hefboom AC met steunpunt F:
    Laat in A een kracht aangrijpen van a1b2
    In C moet dan werken a1b1
    In F werkt a1b2 + a1b1
Beschouw hefboom BC met steunpunt E:
    In B is de kracht a2b1
    en in E a1b1 + a2b1
Beschouw hefboom AB met steunpunt D:
    de kracht in D is a1b2 + a2b1
Beschouw hefboom DC met steunpunt S:
    x1 : x2 = (a1b1) : (a1b2 + a2b1)
    zodat
    x2 : (x1 + x2) = (a1b2 + a2b1) : (a1b1 + a1b2 + a2b1)
Merk op: Voor alle hefbomen wordt dezelfde kracht in S berekend.

Omdat met verhoudingen wordt gewerkt, is het handig teller en noemer nog te delen door a2b2
Stellen we bovendien dat:
    a = a1 : a2
    b = b1 : b2
    x = x2 : (x1 + x2)
dan is
    x = 
    a + b
    a + b + a b
Terug naar het hoofdprobleem
Per punt P, Q, T, U kan nu de x waarde uit a en b worden bepaald.
Zie de tabel hieronder:

    puntabx
    P1/213/4
    Q1/21/24/5
    T221/2
    U123/5
Nu passen we de hulpstelling toe:
    [UTC] : [DMC] = (CU:CD) * (CT:CM) =
    3
    5
     · 
    1
    2
     = 
    3
    10
    [PQC] : [DMC] = (CP : CD) * (CQ : CM) =
    3
    4
     · 
    4
    5
     = 
    3
    5
    [PQTU] :[DMC] = [PQRSTU] : [DEC] =
    3
    5
     − 
    3
    10
     = 
    3
    10
En aangezien
    [DEC] : [ABC] = 1 : 3
    [PQRSTU] : [ABC] = 1 : 10
De zeshoek PQRSTU is dus het tiende deel van driehoek ABC