

| Lastig meetkunde probleem |  |
Verzoek
Ik publiceer hieronder oplossingen van een meetkundig probleem.Typen oplossingen zijn analytisch(numeriek), goniometrisch of geometrisch.
Die laatste oplossing is er (nog) niet.
Lukt u dat wel of heeft u een nieuwe kijk op dit probleem: ik hoor het graag om uw oplossing te publiceren.
Bij voorbaat dank!
Probleem
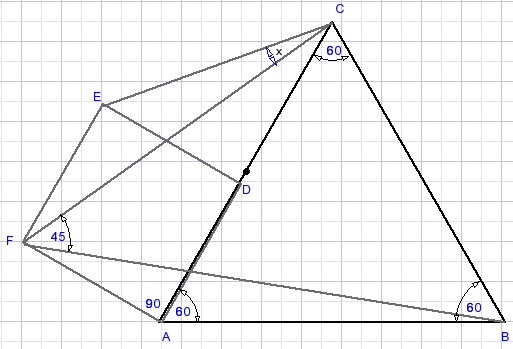
Hierboven staat een regelmatige driehoek ABC met vierkant ADEF.
LBFC=45o.
Gevraagd: bewijs dat LECF=15o.
Allereerst komt de vraag op hoe je deze figuur construeert.
Dat gaat zo:
-
- construeer punt G op midden van AB.
- verleng zijde BA.
- cirkel GC 90o linksom vanuit G.
- HG=GC.
- construeer cirkel door punten H, B, C.
- punt F op cirkel zo, dat LHAF=30o dus AF loodrecht op AC.
- cirkel AF rechtsom, snijpunt met AC is D.
- cirkel AF om rond F en D, snijpunt is E.
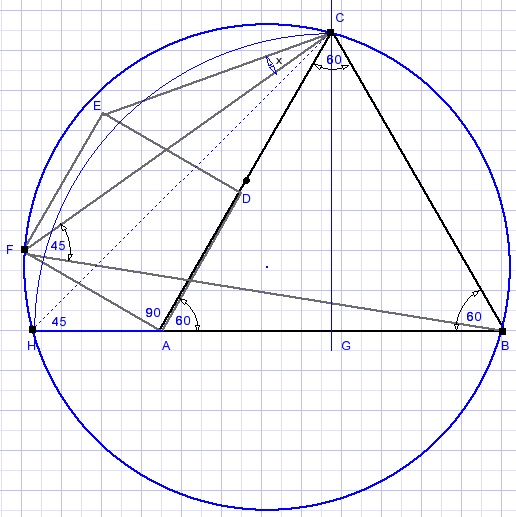
LCHB = LCFB dus liggen op de cirkel.
Numerieke oplossing
(van mijzelf)We stellen AF=2 en AB=2p.
Uit LBFC=45o is dan p te berekenen.
Met de waarde van p zijn de coŲrdinaten van punten C,E,F te berekenen.
Daarmee is Lx (LECF) te bepalen.
Bij deze berekeningen is het handig complexe getallen te gebruiken.
Kijk [ hier] voor de rekenregels van complexe getallen.
De berekening van p
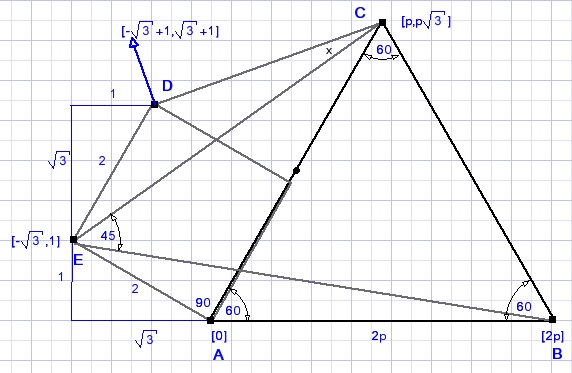
Punt A nemen we als oorsprong(0,0).
De coŲrdinaten van de andere punten volgen eenvoudig.
We vermenigvuldigen vector EB met (1+i) wat 45 graden rotatie geeft.
Deze productvector moet hetzelfde argument hebben als vector EC.
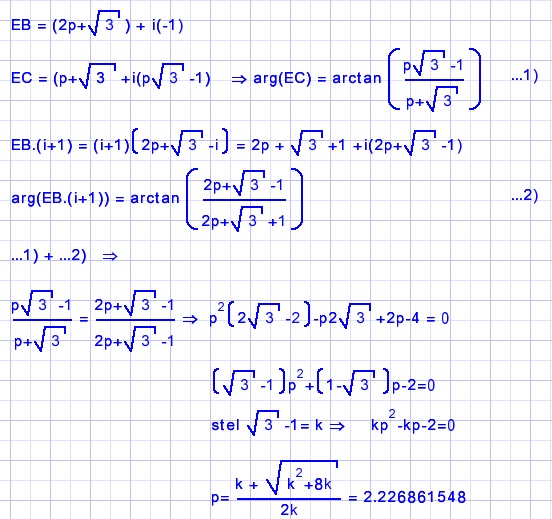
Lx = LECD is verschil van de argumenten van vectoren CE en CD.
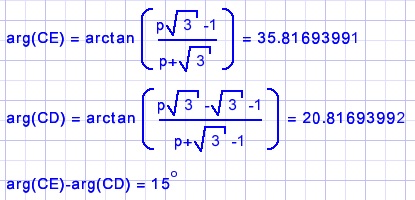
Lx=LDCE=15o
Hulp ingeroepen
Dit probleem gepost in Facebook groep "Classical Mathematics".Hieronder de reacties:
Reactie (1)
Dejan Piscevic.Hij past de sinusregel toe in drie driehoeken en verkrijgt drie vergelijkingen
met de drie onbekenden: x, b en z.
en geeft x=150 als oplossing.
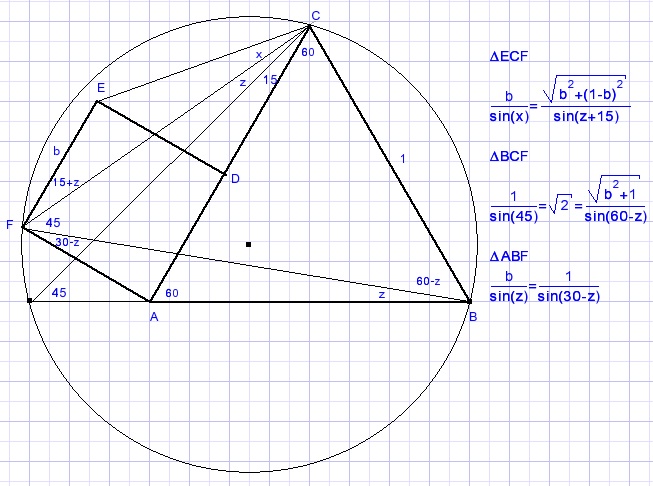
De berekeningen werden niet vermeld.
Volgende aanpak
(van mijzelf)Ik ga verder met de figuur hierboven om b te berekenen.


Nu is nog niet duidelijk of Lx exact 150 is.
Daarvoor moeten we in de waarde van b en tan(x) de wortels laten staan zodat geen afronding plaatsvindt.
Construeer gelijkzijdige driehoek AMD, M op AB.
Teken cirkel met middelpunt M door punten E en F.
Punt C ligt ook op deze cirkel.
Bewijs:
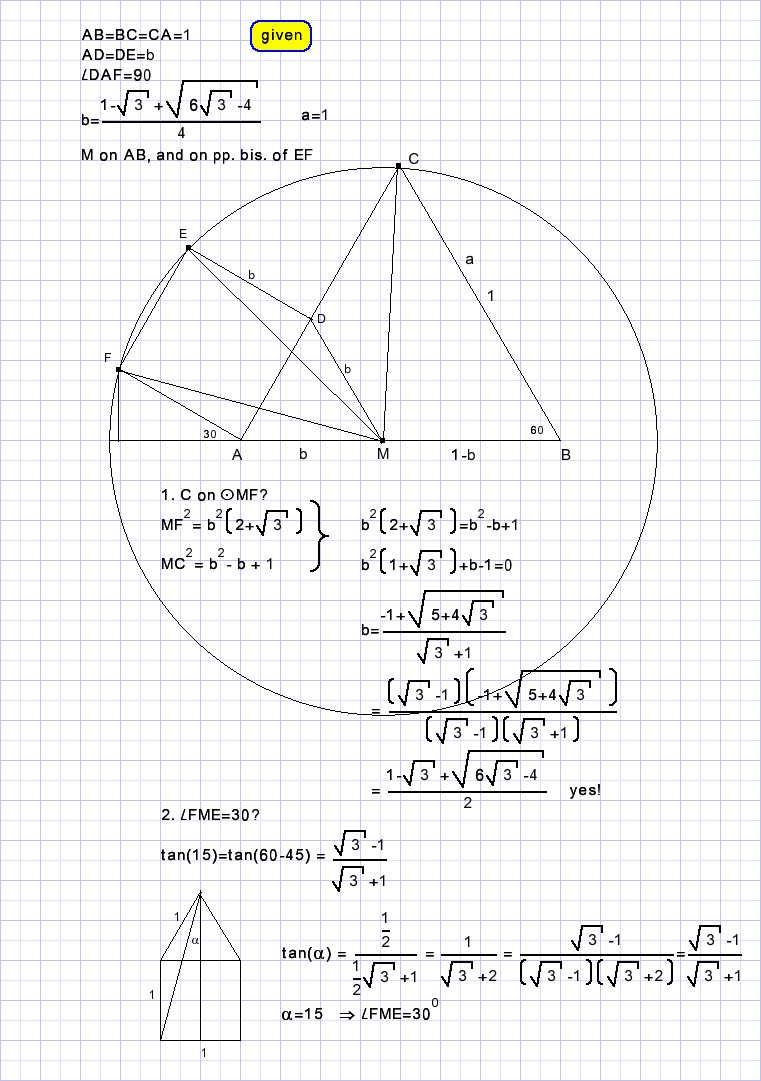
LECF staat op cirkelboog EF zodat Lx = 30/2 = 150.
Reactie (2)
Wong Sii Hiang: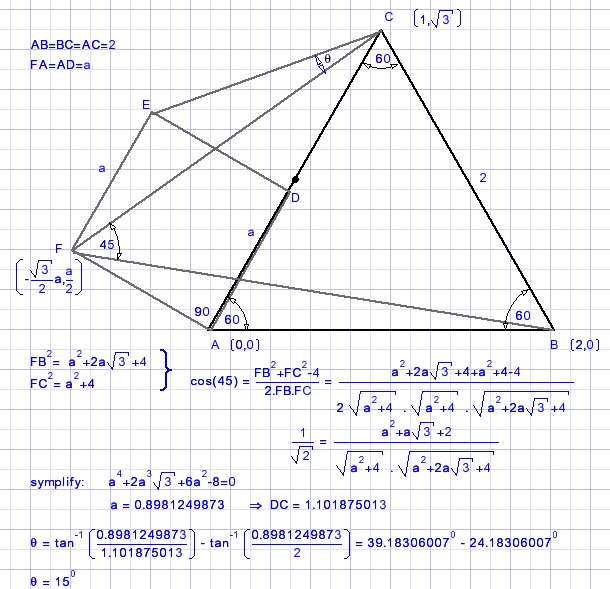
Reactie (3)
Hans Karl Abele: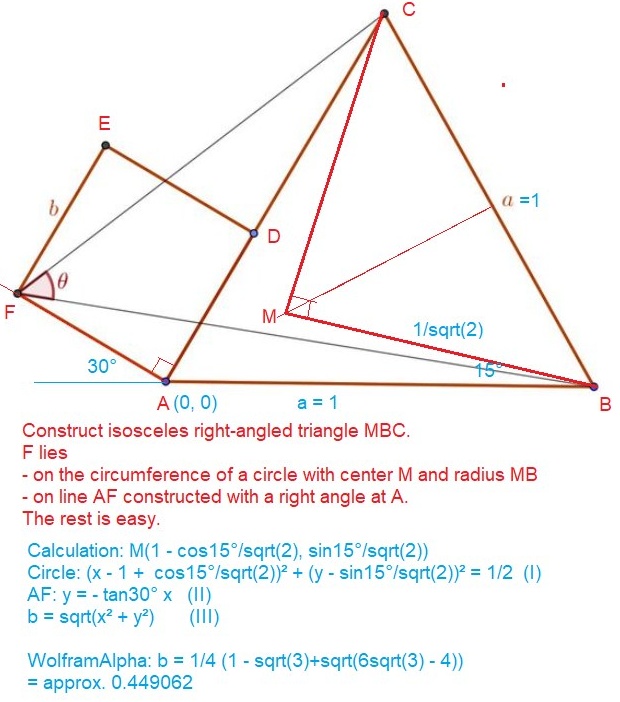
Reactie (4)
Biro Istvan :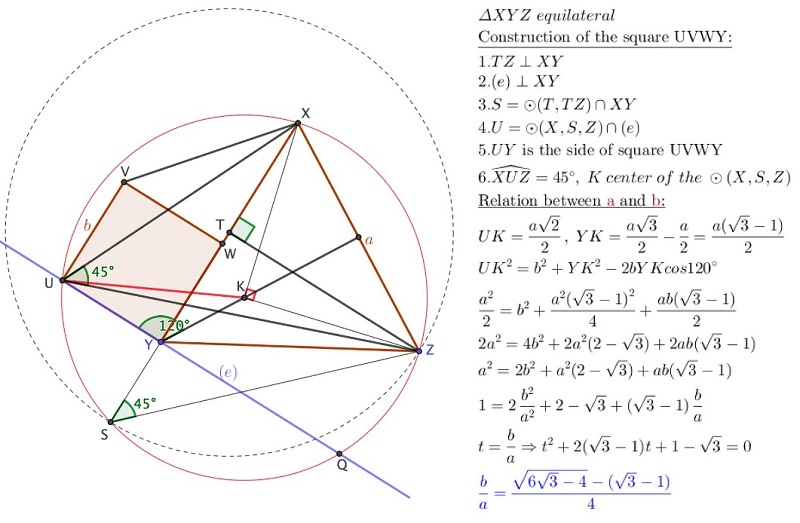
Reactie (5)
Viktor Martoni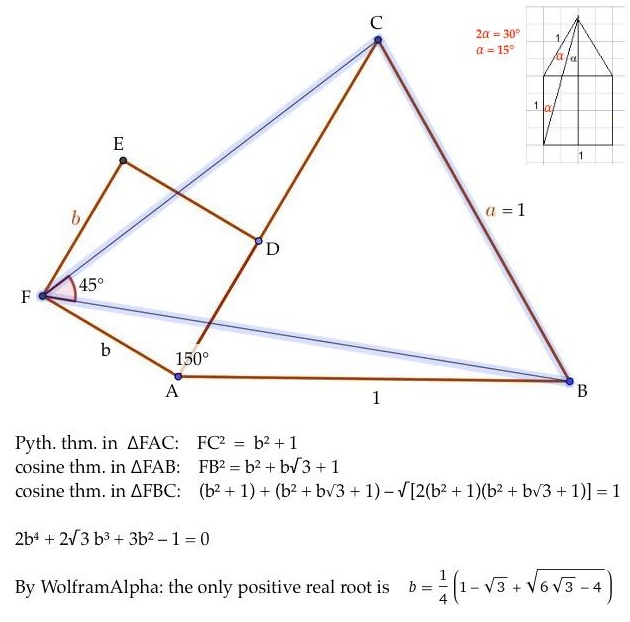
Reactie (6)
Joszef Nagy Vonnak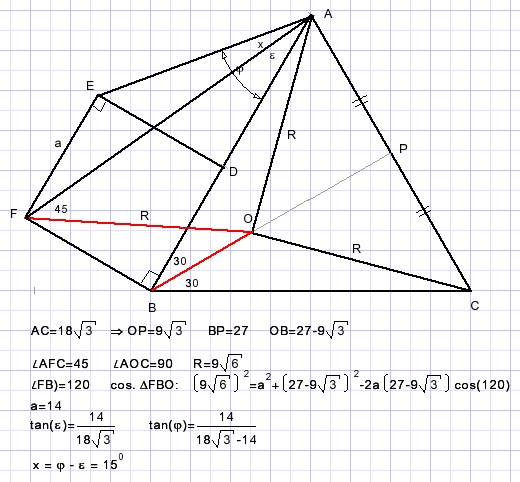
Appendix
Rekenen met complexe getallen.Een lijnstuk stellen we voor als som van een horizontaal- en een vertikaal deel.
Zie de figuur hieronder.
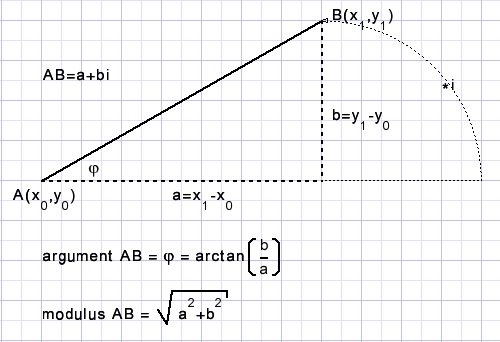
Lijnstuk (vector) AB schrijven we AB=a+bi.
a heet het reeŽle deel, b het imaginaire deel.
b is vermenigvuldigd met operator i, waarvoor de rekenregel geldt: i2= -1.
Reden: vermenigvuldigen met i draait een lijnstuk 90 graden linksom.
Twee achtereenvolgende vermenigvuldigingen met i hebben het effect van -1,
dat is draaiing linksom over 180 graden.
Dit is maf gereken, maar het klopt.
Met de modulus bedoelen we de lengte van het lijnstuk.
Het argument is de hoek met de naar rechts lopende horizontale lijn.
Som en verschil
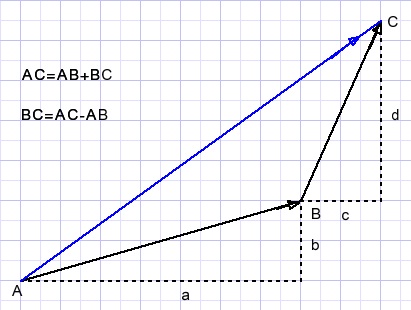
(a+bi) + (c+di) = (a+c) + (b+d)i.
(a+bi) - (c+di) = (a-c) + (b-d)i.
ReeŽle- en imaginaire delen optellen of aftrekken.
Product en quotient
(a+bi)(c+di) = (ac-bd) + (ad+bc)i.
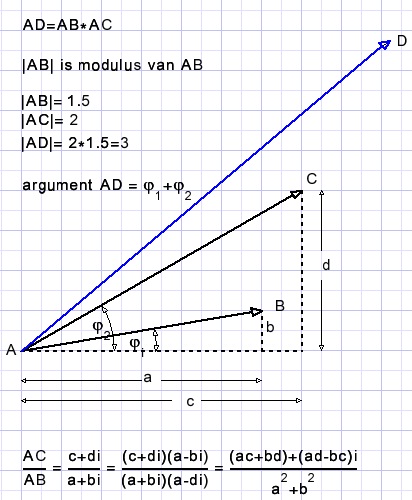
Het effect van vermenigvuldigen is:
-
de modulus is de vermenigvuldiging van beide moduli
het argument is de optelling van beide argumenten.
-
de modulus is het quotient van de moduli.
het argument is het verschil van de argumenten.
Voor uitleg en bewijs verwijs ik naar: davdata.nl/complex

