Complexe Getallen

Inleiding

Bekijk eens figuur 1 hieronder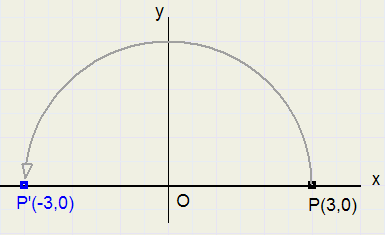
    fig.1
In een rechthoekig coördinatenstelsel is het punt P(3,0) getekend.
Beschouw nu lijnstuk OP met lengte 3 op de X-as.

Ook is het punt P' getekend met coördinaten (-3,0).
OP' is ontstaan uit OP door de x-coördinaat te vermenigvuldigen met -1.
Vermenigvuldigen met -1 komt dus neer op een draaiing van +180 graden.
We spreken af, dat een positieve draaiing tegen de klok in is.

Draaien we twee maal over 180 graden, dan zijn we weer op het uitgangspunt terug.
Rekenkundig komt dit overeen met: -1 * -1 = +1.

We voeren nu een getal i in met de eigenschap dat een lijnstuk 90 graden (linksom) draait
als we met i vermenigvuldigen.
Het getal i heeft dan de merkwaardige rekenregel dat i2= -1
Immers, twee maal 90 graden draaien is hetzelfde als 180 graden draaien.

Na 90 graden draaien wijst OP in de positieve richting van de y-as.
Noemen we dit punt Q dan heeft Q de coördinaten (0, 3i)
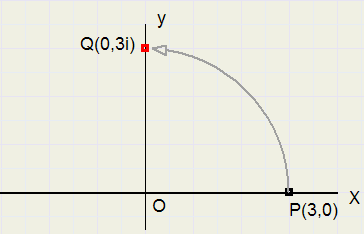    fig.2
In figuur 3 hieronder staat een willekeurig punt P(a,b) in een assenstelsel.
Vatten we de Y-as op als een 90 graden gedraaide X-as, dan moet de y waarde
worden vermenigvuldigd met i.
Het punt P is dan te schrijven als P(a + bi), namelijk de optelling van a en de 90 graden gedraaide b.

a + bi heet een complex getal.
a is het reële deel, b heet het imaginaire deel.
a en b zijn beide reële getallen.
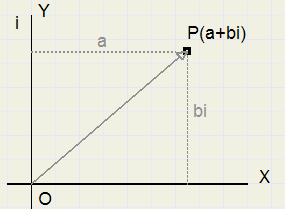    fig.3
Het aldus ontstane coördinatenstelsel noemen we het complexe vlak.
Een punt (of lijnstuk vanaf oorsprong O) is dan aan te geven met één enkel complex getal
bijvoorbeeld z = 3 + 5i.
Hieronder zie je als voorbeeld de punten A t/m F in het complexe vlak.
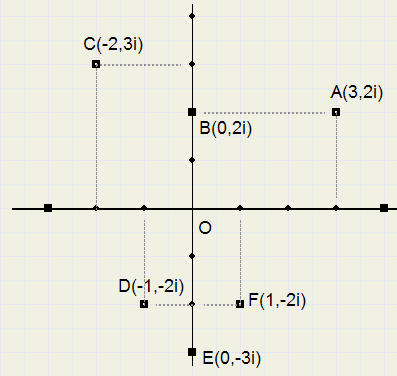    fig.4
Het voordeel van negatieve getallen is, dat behalve de grootte ook de richting is te zien.
Die richting is wel beperkt tot een lijn, dus alleen de tegengestelde richting is mogelijk.
Bij complexe getallen kan de richting variëren van 180 graden tot -180 graden.

Met negatieve getallen kunnen we een punt op een lijn aangegeven als de schaal en de oorsprong bekend zijn.
Met één complex getal is een punt in een coördinatenstelsel aan te geven als de schaal en de oorsprong bekend zijn.

Intermezzo

Hiervoor vermenigvuldigden we lijnstuk OP met i waarbij P was gelegen op de X-as.
Maar zou lijnstuk OP ook 90 graden draaien als P willekeurig in het complexe vlak ligt?
Stel P(z) waarbij z = 4 + 7i
Vermenigvuldigen met i levert dan op
    i.z = i (4 + 7i) = 4i + 7.i.i = -7 + 4i
Zie figuur 5 hieronder.
Voor Q geldt Q(-7+4i).
Opnieuw vermenigvuldigen
    i(-7 + 4i) = -4 - 7i, wat het punt R is
    i(-4 - 7i) = 7 - 4i, het punt S en
    i(7 - 4i) = 4 + 7i , punt P opnieuw, we zijn rond.
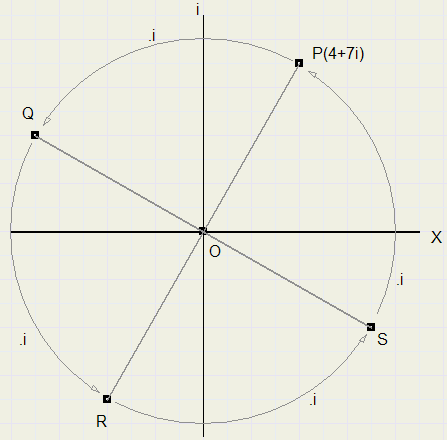    fig.5
Dat geeft wat vertrouwen in deze merkwaardige manier van rekenen.

De grootte van een complex getal

Als complex getal z = a + bi dan is de grootte van z de lengte van Lijnstuk OP.
Die grootte heet ook wel de modulus , geschreven |z|.

Met de stelling van Pythagoras zien we dat
    |z| = | a + bi| =
    \a 2 + b 2
     .........zie figuur 3.
oftewel:
    de modulus van een complex getal is de wortel uit de som van de kwadraten
    van het reële en het imaginaire deel

Voorbeeld:
|11 + 5i| =
\11 2 + 5 2
 = 
\146



De richting (argument) van een complex getal

De richting van een complex getal kan variëren van 180 graden (linksom +), tot -180 graden (rechtsom -).
Noemen we de richting van complex getal z = a + bi ....... arg(z) dan geldt
    arg(z) = arctan(
    b
    a
     ).............de omgekeerde tangens functie
rekenen we niet in graden maar in radialen dan geldt:
    -p < arg(z) £ p
Het argument van een complex getal is de hoek met de positieve x-richting.

De som van twee complexe getallen

Als
    z = a + bi
    w = c + di...............dan

    z + w = a + bi + c + di = a + c + i(b + d)
De reële- en ook de imaginaire delen van z en w moeten worden opteld.
De figuur hieronder laat dat zien
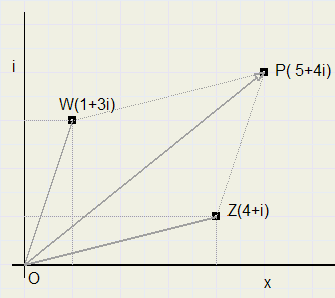    fig.6
In fig.6 hierboven is OP = OW + OZ

Het verschil van twee complexe getallen

Als
    w = a + bi
    z = c + di...............dan

    w - z = a + bi - ( c + di) = a - c + i(b - d)
Van zowel het reële- als het imaginaire deel moet het verschil worden genomen.
Zie figuur 7 hieronder
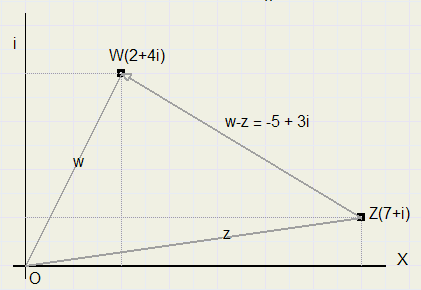    fig.7
In fig.7 hierboven is ZW = OW - OZ

merk op: "verschil" is altijd wat toegevoegd moet worden om van het begin naar het eindpunt te komen.



Het product van twee complexe getallen

Als
    w = a + bi
    z = c + di...............dan

    w.z = (a + bi)(c + di) = ac + adi + bci - bd............................{ want i.i = -1}
    w.z = ac - bd + i(ad + bc)
We zien een reëel deel : ac - bd en een imaginair deel ad - bc
Wat moeten we hier nu mee aan?

Eerst eens kijken naar de moduli:
    |w| =
    \a 2 + b 2
    |z| =
    \c 2 + d 2
    |w.z| =
    \(a c − b d) 2 + (a d + b c) 2
     ..................haakjes weg.........
    |w.z| =
    \a 2 c 2 − 2 a b c d + b 2 d 2 + a 2 d 2 + 2 a b c d + b 2 c 2
     ..................vereenvoudigen
    |w.z| =
    \a 2 c 2 + b 2 d 2 + a 2 d 2 + b 2 c 2
     .................buiten haakjes halen a2 en b2
    |w.z| =
    \a 2 (c 2 + d 2) + b 2 (d 2 + c 2)
     .................als factoren schrijven
    |w.z| =
    \(a 2 + b 2) (c 2 + d 2)
     = 
    \a 2 + b 2
     
    \c 2 + d 2
De modulus van het product is het product van de moduli van de complexe getallen.

Nu beschouwen we het argument van |w.z|
    arg(w) = arctan(
    b
    a
     )
    arg(z) = arctan(
    d
    c
     )
Stel nu
    a = arg(w).........en
    b = arg(z).........dan geldt
    tan(a) =
    b
    a
    tan(b) =
    d
    c
Van de goniometrie is de volgende formule bekend voor de tangens van de som van twee hoeken
    tan (a + b) = 
    tan a +  tan b
    1 −  tan a ·  tan b
Invullen van tan(a) , tan(b) levert op:
     
    tan (a + b)
         		 
     = 
     
    b
    a
     + 
    d
    c
    1 − 
    b
    a
     · 
    d
    c
     ................vereenvoudigen
    tan (a + b) = 
    a d + b c
    a c − b d
Maar dat komt ons bekend voor:
in de teller staat het imaginaire- en de de noemer het reële deel van het product.
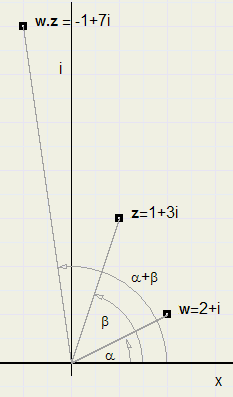
Conclusie
    Het argument van de product van twee complexe getallen is de som van hun argumenten
Figuur 8 hieronder geeft een voorbeeld
    fig.8
Merk op:
Als we een lijnstuk willen roteren dan dient dus te worden vermenigvuldigd met een complex getal met
een modulus van 1 anders verandert de grootte.

Het quotient van twee complexe getallen

Omdat delen het omgekeerde is van vermenigvuldigen kunnen we concluderen bij twee complexe getallen dat:
    De modulus van het quotient het quotient is van de moduli van de getallen
    Het argument van het quotient het verschil is van de argumenten
De lezer mag dit zelf nagaan.

De complexe noemer van een breuk reëel maken

Stel dat we een formule tegenkomen als
    4 + 7 i
    2 − 3 i
De i is dan eenvoudig uit de noemer te verwijderen door teller en noemer te vermenigvuldigen met 2+3i
    (4 + 7 i) (2 + 3 i)
    (2 − 3 i) (2 + 3 i)
     = 
    8 + 12 i + 14 i − 21
    4 + 6 i − 6 i + 9
     = 
    −13 + 26 i
    13
     = −1 + 2 i
2 + 3i heet de geconjugeerde van 2 - 3i.
De geconjugeerde van een complex getal verkrijg je door het teken van het imaginaire deel om te draaien.

Poolcoördinaten

In een rechthoekig assenstelsel wordt de positie van een punt P gegeven door de afstanden tot de y- en de x-as.
Bij poolcoördinaten wordt de positie van een punt P aangegeven met de afstand tot de oorsprong (O) en
de de hoek van OP met de positieve x-richting.
In een complex vlak met poolcoördinaten met punt P(z) waarbij z= a + bi zien we
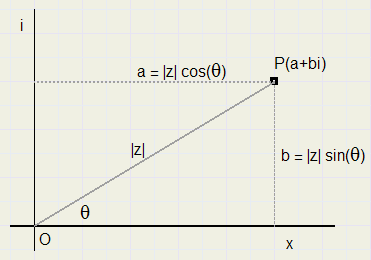    fig.9
Het complexe getal z = a + bi is met poolcoördinaten te schrijven als
    |z|(cos θ + i sin θ ) ........waarbij |z| de modulus is en θ het argument
Vermenigvuldigen met (cos θ + i sin θ) draait dus een vector θ graden linksom bij gelijkblijvende grootte.
Merk op, dat sin2θ + cos2θ = 1.

Uit het bovenstaande volgt meteen de Stelling van de Moivre:
    (cos θ + i sinθ)n = cos n.θ + i sin n.θ

Vergelijkingen met complexe variabelen

Een eenvoudige vergelijking is bijvoorbeeld
    z2 + 1 = 0..................ontbinden in factoren...
    (z - i)(z + i) = 0
    of z = i.........of z = -i
We hadden ook kunnen schrijven
    z2 = -1............wortel trekken
    z =
    \−1
    z = i
Merk op:
1.
    i2 = -1.........zodat
    i = +-
    \−1
    maar afspraak is dat de negatieve wortel niet gebruikt wordt.
    Dat zou maar verwarring geven, als i zowel de waarde - als +
    \−1
     zou hebben.
2.
    \−5
     = 
    \5.i 2
     = i 
    \5

Nu de vergelijking
    z3 =1.........of
    z3 - 1 = 0.......ontbinden in factoren.....
    (z - 1)(z2 + z + 1) = 0
    of
    z = 1
    of
    z2 + z + 1 = 0.......abc formule.........
    z =
    −1 + −
    \−3
    2
    z = −
    1
    2
     + i · 
    1
    2
     
    \3
    of
    z = −
    1
    2
     − i · 
    1
    2
     
    \−3
De modulus hiervan is 1, we hadden niet anders verwacht.
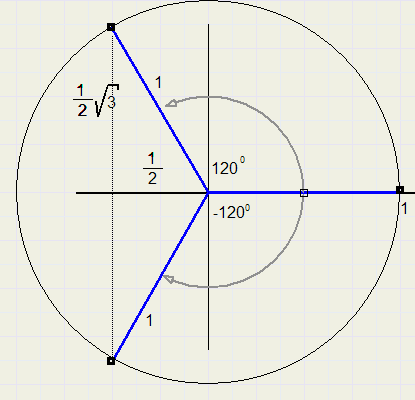
Het argument is 120 of 240 (-120) graden.
Zie de figuur10. hieronder:
    fig.10
Het idee komt nu op, dat in het complexe vlak een n-de graads vergelijking n oplossingen heeft.

Bovenstaand vraagtuk had ook anders opgelost kunnen worden.
Uit de stelling van de Moivre volgt namelijk meteen
    n
    \    		 cos q + i ·  sin q
     =  cos
    æ
    q
    n
    		ö
    ­­
    èø
     + i ·  sin
    æ
    q
    n
    		ö
    ­­
    èø
    bedenkend, dat θ = θ + k.360 ......waarbij k = 1,2,3,....schrijven we
    n
    \    		 cos q + i ·  sin q
     =  cos
    æ
    q + k · 360
    n
    		ö
    ­­
    èø
     + i ·  sin
    æ
    q + k · 360
    n
    		ö
    ­­
    èø
    zodat in het geval van n = 3 en z = 1 (θ = 0) :
    3
    \    		 cos q + i ·  sin q
     =  cos
    æ
    k · 360
    3
    		ö
    ­­
    èø
     + i ·  sin
    æ
    k · 360
    3
    		ö
    ­­
    èø
     =  cos (k · 120) + i ·  sin (k · 120)

Voorbeelden

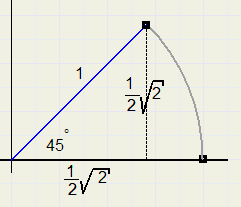
a.
Met welk complex getal moet worden vermenigvuldigd om een vector 45° linksom te laten draaien?

stel het getal is z = a + b i of cos(φ) + i.sin(φ) want de modulus moet 1 zijn.
Zie figuur 11.
sin(φ) = cos(φ) =
1
2
 
\2
zodat
z =
1
2
 
\2
 +
1
2
 
\2
 .i
    fig.11
b.
Met welk complex getal moet worden vermenigvuldigd om een vector 50° rechtsom te laten draaien
en tevens te verdubbelen in grootte?

Stel het getal is z = a + bi = 2(cos(φ) + i.sin(φ))
Gebruik de rekenmachine om 2sin(-50°) = -1,532 en 2cos(-50°) = 1,286 te berekenen.
Het gezochte getal is dus z = 1,286 - i.1,532

c.
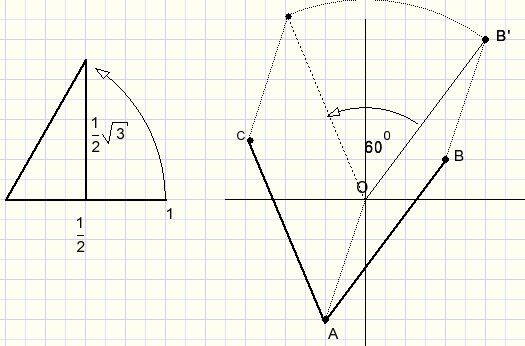
Een gelijkzijdige driehoek ABC heeft als basis de punten A(-1,-3) en B(2,1).
Bereken de coördinaten van hoekpunt C.

AB is een vector met modulus
\(1 − −3) 2 + (2 − −1) 2
 = 5
Verschuif nu AB evenwijdig zodat punt A in de oorprong ligt en B op B'(3+4i).
OB' moet 60 graden linkom of rechtsom worden gedraaid.
Dat geschiedt door vermenigvuldiging met
1
2
 + 
1
2
 i 
\3
 ......60 graden linksom
of
1
2
 − 
1
2
 i 
\3
 ......60 graden rechtsom
linksom:
⎧
1
2
 + 
1
2
 i 
\3
⎫
⎩⎭
 (3 + 4 i) = 
3
2
 − 2 
\3
 + i 
⎧
3
2
 
\3
 + 2		⎫
⎩⎭
afgerond: -1,96 +4,6i
deze waarde optellen bij A(-1-3i) levert op C(-2,96 + 1,6i).
Zie figuur 12: