De energie van een vliegwiel

Uitgangspunt is de formule voor de kinetische energie van een massa m (kg),
die met snelheid v (m/s) voortbeweegt:



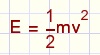
De afleiding van deze formule staat hier

Het probleem bij een vliegwiel is dat de snelheid van elk punt afhankelijk is van de afstand tot het middelpunt.
We beschouwen een concentrisch cirkeltje met straal r en dikte Dr.
(in de figuur aangegeven met groen)



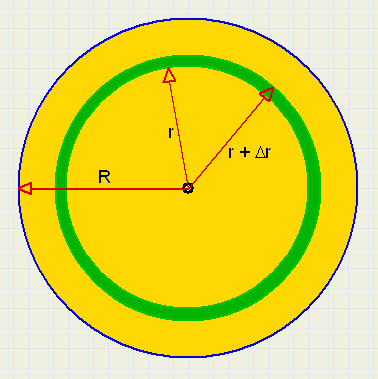
We nemen aan, dat alle groene massa dezelfde snelheid heeft.
Het materiaal heeft verder een dichtheid r (kg/m3).
De dikte van het wiel is d (meter).
De massa van een schilletje of afstand r van het draaipunt is dan
    Dm = 2pr.d.Dr.r

Bij n omwentelingen per seconde is de snelheid op afstand r van het midden
    v = 2pr.n

combinerend, is de energie in het schilletje op afstand r van het draaipunt:
    DE = 4p3drn2r3Dr
zodat


    E = p3drn2R4....geïntegreerd van 0...R
Nu is de totale massa M van het wiel
    M = pR2rd
wat de formule vereenvoudigt tot
    E = Mn2p2R2
    E = M(pRn)2
Nu is de snelheid v van een punt op de omtrek
    v = 2pRn
zodat


De dichtheid van beton is ongeveer 2500 kg/m3.
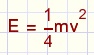
Laten we in ons huis een betonnen vliegwiel installeren met een straal van 1 meter en een dikte van 50cm.
Als het vliegwiel draait met 25 omwentelingen per seconde dan is de opgeslagen energie:
    E = 0,25 . 2500 . 3,14 . 0,5 . (25 . 2. 3,14)2 = 24MJ = 6,7KWh.