

| Eenheden en energie |  |
Dit artikel beperkt zich tot mechanische energie.
Meten is eenheden tellen.
In de natuurkunde wordt het Giorgi stelsel gebruikt, een internationaal stelsel van eenheden.
De eenheid van afstand (s) is de meter.
De eenheid van tijd (t) is de seconde.
Hieruit volgt de dimensie van snelheid (v) : meter/seconde
Een voorwerp dat gedurende t seconden beweegt met snelheid v legt een afstand af van
-
s = vt
Versnelling (a) is verandering van snelheid per tijdseenheid.
De dimensie van versnelling is snelheid/seconde, dus afstand/seconde/seconde = afstand/seconde2
Een voorwerp dat vanuit stilstand gedurende een tijd t een versnelling a ondergaat heeft een snelheid
-
v = at
De zwaartekracht op aarde geeft een voorwerp een versnelling van 9,8m/s2.
Die zwaartekrachtversnelling wordt in formules met de letter g aangegeven.
Welke weg heeft een voorwerp afgelegd als het vanuit stilstand
gedurende t seconden een versnelling a ondergaat?
Bekijk daarvoor het grafiekje hieronder:
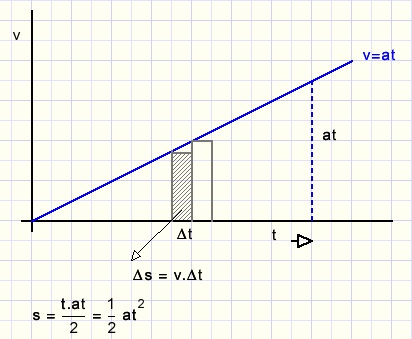
Gedurende een heel kleine tijd Δt stellen we de snelheid constant.
In die kleine tijd wordt dan een afstand Δs afgelegd.
Door de tijdvakjes steeds kleiner te maken naderen we tot de oppervlakte van de driehoek,
dat is dus precies de totaal afgelegde weg s.
De eenheid van massa is de kilogram.
Kilogram kennen we al als gewicht, maar dat hangt af van de plaats in het universum.
Een liter water heeft een massa van 1 kg., dat geldt op aarde maar ook op de maan.
De zwaartekracht op de maan is ťťn zesde deel van die op aarde.
De eenheid van kracht (F) is de Newton.
1 Newton is de kracht die een massa van 1kg. een versnelling geeft van 1m/s2.
Hier geldt de formule:
-
F = ma
De versnelling is recht evenredig met de kracht die op een massa wordt uitgeoefend.
De eenheid van energie (E) is de Joule (J)
Mechanische energie leveren we door een kracht over een bepaalde afstand uit te oefenen.
Bijvoorbeeld door een autoband te verslepen.
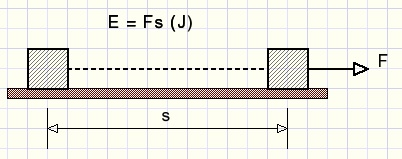
Stel uw gewicht (massa) is 75kg.
Om traplopend de volgende verdieping (h = 2,5meter hoger) te bereiken kost een energie:
-
E = F.h = mgh = 75.9,8.2,5 = 1838J.
1 Watt is 1 Joule per seconde.
E = P.t
P = E/t
Om de voorgaande trap in 5 seconden te beklimmen is een vermogen nodig van
-
P = 1838/5 = 367Watt.
Een kaarsvlammetje heeft een vermogen van zo'n 100Watt, dat is evenveel als een mens in rust
nodig heeft voor lichaamsverwarming en de hartspier.
Er zijn twee soorten mechanische energie:
1.PotentiŽle energie
E = mgh
Een massa m is hier tegen de zwaartekracht in h meter opgetild.
2. Kinetische energie
Een massa waarop een kracht werkt versnelt.
Welke energie bevat een massa die met snelheid v voortbeweegt?
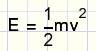
Bewijs:
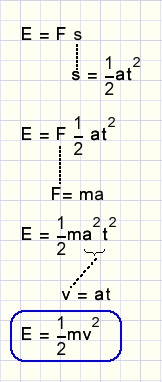
Toepassingen.
1.
Van een 60 meter hoge kerktoren laten we een kei omlaag vallen.
a. Met welke snelheid raakt de kei de grond?
b. Hoe lang duurt de val?
We ronden de zwaartekrachtsversnelling even af op 10m/s2
s = 0,5 a t2
60 = 0,5.10.t2
t = 3,46 sec.
v = at
v = 10. 3,46 = 34,6m/s
Anders:
De kei heeft een potentiŽle energie E = mgh = m.10.60 (J)
Beneden aangekomen is die energie omgezet in kinetische energie E = 0,5mv2
600m = 0,5mv2
v = 34,6m/s.
v = at = 10t
t = 34,6 / 10 = 3,46 sec.
2.
De beweging van een recht omhoog geschoten kogel is op te vatten als de som van twee bewegingen:
a. een met gelijkblijvende snelheid (van afschieten)
b. een valbeweging.
We schieten een kogel recht omhoog af met snelheid v.
Welke hoogte wordt bereikt?
Stel de kinetische energie bij afschieten gelijk aan de potentiŽle energie op het hoogste punt:
mgh = 0,5mv2
h = 0,05v2
Bij v = 300m/s is h = 4,5km.
Als de kogel onder een hoek α met het aardoppervlak wordt afgeschoten dan is:
de vertikale snelheid v.sin(α)
de horizontale snelheid v.cos(α)
3.
Onder welke hoek moet een kogel worden afgeschoten om zover mogelijk neer te komen?
De vertikale snelheid neemt elke seconde af met 10m/sec,
dus in t = v.sin(α) /10 seconden wordt het hoogtste punt bereikt.
Daarna is dezelfde tijd nodig voor de afdaling.
In die tijd beweegt de kogel horizontaal een afstand s = v.cos(α).2t, zodat
s = 2.v.sin(α) . 0,1 . v.cos(α)
s = 0,1v2sin(2α)
s heeft de grootste waarde voor sin(2α)=1 zodat
α = 45 graden.

