De stelling van Ptolemaeus

Ptolemaeus leefde rond het begin van de jaartelling in Alexandrië.
Aan hem danken we de volgende stelling uit de vlakke meetkunde:
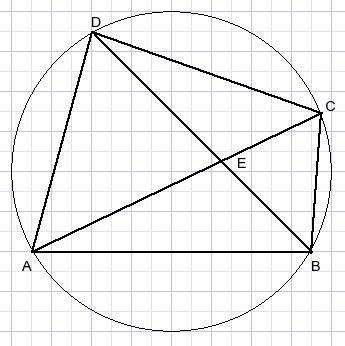
    In een koordenvierhoek is het product van de diagonalen gelijk aan de som van de
    producten van de tegenoverliggende zijden.
In beeld:


    AC.BD = BC.AD + AB.CD
In dit artikel vermeld ik het bewijs van deze stelling plus een toepassing.

Daarbij maak ik gebruik van gelijkvormigheid van driehoeken, de stelling van Thales en de stelling van Stewart.

Korte herhaling

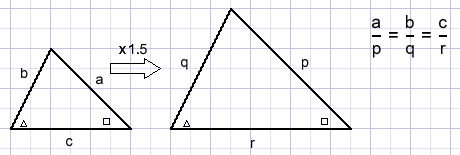
Gelijkvormigheid
Driehoeken met gelijke hoeken zijn gelijkvormig dwz de een is een vergroting van de ander:



Stelling van Thales



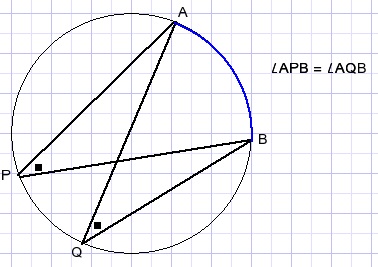
De gemerkte hoeken zijn gelijk omdat ze op dezelfde cirkelboog AB staan.
De Stelling van Thales is uitgebreider, kijk [HIER] voor het bewijs en meer.

Stelling van Stewart



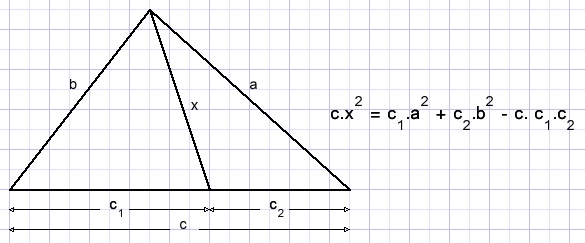
Het bewijs staat [HIER]

De stelling van Ptolemaeus




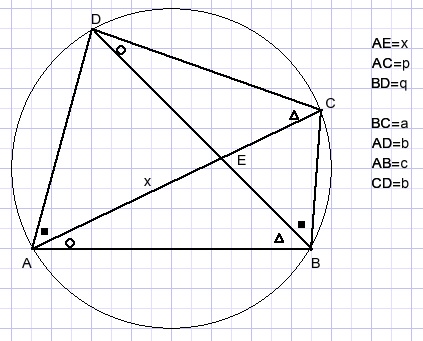
Te bewijzen is:
    p.q = a.b + c.d
Gelijke hoeken zijn gelijk gemerkt (stelling van Thales).
We gaan uit van AE=x en berekenen lijnstukken BE en DE
waarna we de stelling van Stewart toepassen in driehoek ABD.



Toepassing


Hieronder staat een regelmatige 7-hoek met een intrigerend verband.



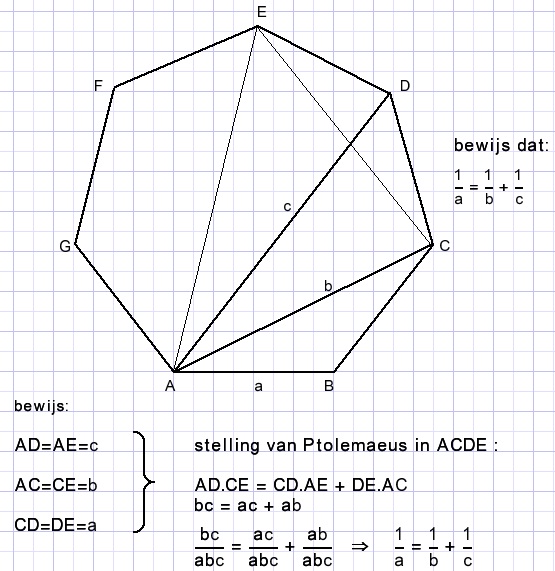
Een eenvoudig bewijs, dankzij de stelling van Ptolemaeus.

Dit probleem vond ik in een Facebook wiskunde groep.
De oplossing was van Kenny Lao.