Uitwerking meetkunde constructies

1.

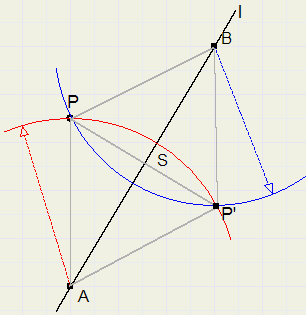
Gegeven is een lijn l met daarbuiten een punt P
Spiegel P in lijn l. (noem spiegelpunt P').
Voor deze constructie is een passer voldoende.

Kies punten A en B op l (niet te dicht bij elkaar)
Cirkel afstand AP om vanuit A, cirkel BP om vanuit B.
P' is het snijpunt van de cirkels.

Driehoeken APB en AP'B zijn congruent. (ZZZ)
Dus LPAB = LP'AB
Dus driehoeken PAS en P'AS zijn congruent (ZHZ)
Dus PS = SP' en PP' staat loodrecht op l

2.

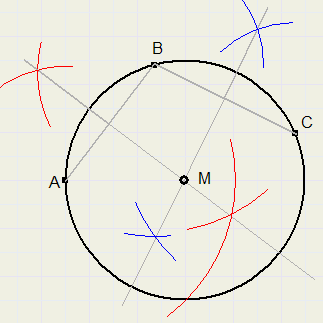
Gegeven is een cirkel.
Construeer het middelpunt.

Kies punten A, B en C op de cirkel (niet te dicht bij elkaar).
Trek lijnen AB en BC.
Construeer middelloodlijnen van AB en BC.
Middelpunt M is het snijpunt van de middelloodlijnen.

Punten op de middelloodlijn van AB liggen evenver van A als B.
Punten op de middelloodlijn van BC liggen evenver van B als van C.
Snijpunt M ligt evenver van A, B en C.

3.

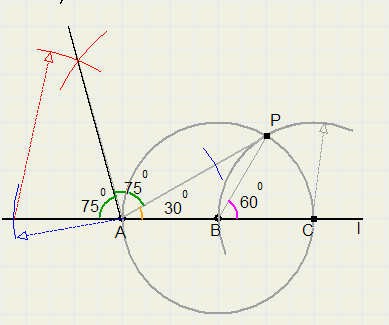
Construeer een hoek van 75 graden.

75 = (180 - 30) / 2
Trek lijn l en plaats daarop punten A en B.
Cirkel BA om vanuit B. Noem snijpunt l met cirkel C.
Cirkel BA om vanuit C. Noem snijpunt van de cirkels P.
LPAC = 30 graden.
Construeer deellijn van stompe hoek tussen l en AP

LA₁ = 30 graden, want staat op boog van 60 graden.
LA₂₃ = 180 - 30 = 150 graden.
LA₂ = LA₃ = 75 graden.

4.

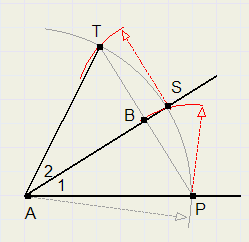
Construeer de verdubbeling van een gegeven hoek.

Gegeven is LA₁.
Trek cirkel om A, noem snijpunten met zijden P en S.
Cirkel afstand PS om vanuit S, snijpunt met cirkel (A) is T.
LTAP = 2 * LA₁

Driehoeken ABT en ABP zijn congruent (ZHZ).

5.

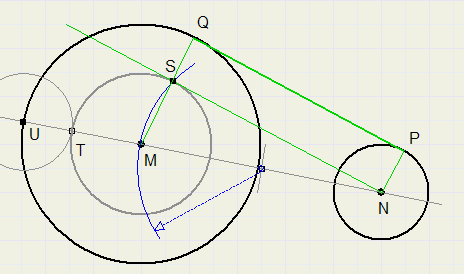
Gegeven zijn twee cirkels met hun middelpunten M en N.
Construeer een lijn die beide cirkels raakt.

Trek lijn door M en N, snijpunt met grootste cirkel is U.
Cirkel kleine cirkel om vanuit U, snijpunt met lijn is T.
Trek hulpcirkel vanuit M met straal MT.
Beschouw MN als middellijn van een cirkel.
Trek deze cirkel(boog). (bepaal midden MN, trek cirkel)
Snijpunt cirkelboog met hulpcirkel is S.
NS is raaklijn aan cirkel M, door punt N.
Trek lijn MS door, snijdt cirkel in Q.
Construeer rechthoek SNPQ.
PQ is de lijn die beide cirkels raakt.

SQ = NP = straal cirkel N.
MQ en NP staan loodrecht op PQ

6.

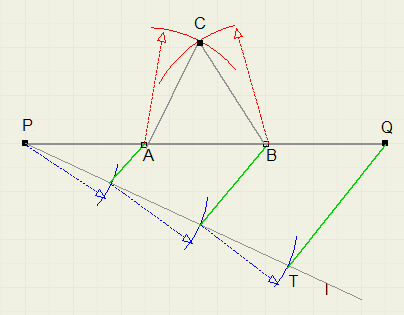
Construeer een gelijkzijdige driehoek als de omtrek is gegeven.

We gaan uit van lijn PQ.
Trek hulplijn l door P en pas 3 gelijke delen af. Laatste punt is T.
Trek TQ en evenwijdige lijnen.
A en B zijn snijpunten evenwijdige lijnen met PQ.
Cirkel afstand AB om vanuit punten A en B. Snijpunt is C.
Teken de gevraagde driehoek ABC

Snijdende lijnen worden door evenwijdige lijnen in stukken
verdeeld met gelijke verhouding.
Daarom is PA = AB = BQ.
AC = BC = AB

7.

Construeer een driehoek ABC als gegeven is
a. de basis AB, LA en de som van de opstaande zijden AC + BC

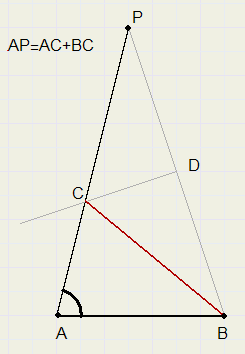
Gegeven zijn AB, AP=AC+BC en LA
Trek BP.
Construeer middellloodlijn van BP.
Snijpunt middelloodlijn met AP is C
In driehoek ABC geldt : AC + BC = AP

Driehoeken PDC en BDC zijn congruent (ZHZ), zodat BC=PC

b. de basis AB, LA en het verschil van de opstaande zijden AC - BC

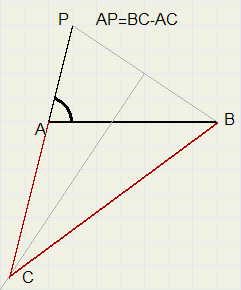
Trek BP.
Construeer middelloodlijn BP.
Bepaal snijpunt C van verlengde AP en middellloodlijn.
ABC is de gevraagde driehoek

C op middelloodlijn, dus PC = BC.
dus AP = BC - AC

c. basishoeken A en B en de som van de opstaande zijden AC + BC

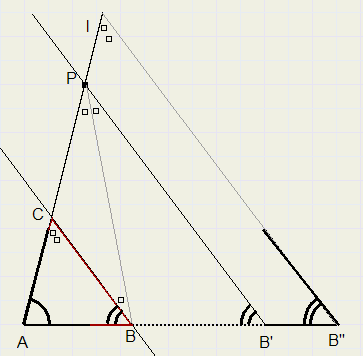
Teken hoek A en (voorlopige) hoek B'' op lijn AB''.
AP is gegeven afstand AC + BC.
Verschuif hoek B'' over AB'', zodat zijde door P gaat.
Verschoven punt B'' is B'.
Construeer deellijn van LAPB', snijpunt met AB' is B.
Trek lijn door B evenwijdig aan B'P, snijpunt met AP is C.
ABC is de gevraagde driehoek

In de figuur staat elk klein vierkantje voor een waarde van
(180 -LA - LB)/2 graden
Driehoek BCP is gelijkbenig, zodat BC = PC

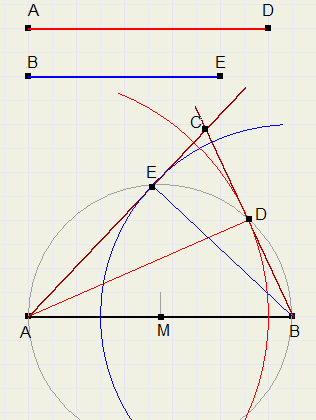
d. basis AB en de hoogtelijnen AD (op BC) en BE (op AC)

Construeer midden M van AB en trek cirkel om M met straal MA.
Cirkel gegeven afstand AD om vanuit A.
Cirkel gegeven afstand BE om vanuit B.
D en E zijn snijpunten met cirkel M.
Trek lijnen door A en E en door B en D.
Snijpunt van deze lijnen is C.
ABC is de gevraagde driehoek.

LAEB = LADB = 90 graden, want staat op middellijn AB.

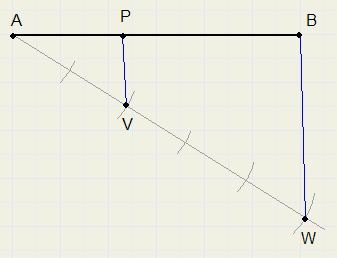
8.

Verdeel een gegeven lijnstuk in delen die zich verhouden als 2 : 3

AB is het gegeven lijnstuk.
Trek hulplijn door A en pas 2 gelijke delen af (punt V).
Pas vanaf V nog 3 gelijke delen af (punt W).
Trek lijn WB en parallel daaraan lijn VP.
P is het gevraagde punt op AB. Trek lijn

Evenwijdige lijnen verdelen snijdende lijnen in delen met gelijke verhoudingen

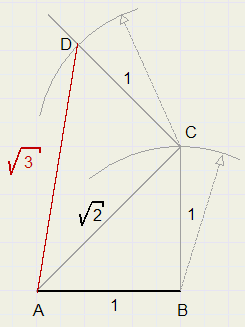
9.

Construeer een lijnstuk met lengte wortel 3, als een lijnstuk met lengte 1 is gegeven.

AB = 1 (gegeven).
Richt loodlijn op vanuit B.
Cirkel AB om vanuit B, C is snijpunt met loodlijn.
Richt loodlijn op AC op vanuit C.
Cirkel afstand AB om vanuit C, D is snijpunt met loodlijn op AC.
AD is de gevraagde lijn.

Pas stelling van Pythagoras toe in driehoeken ABC en ACD

10.

Construeer rechthoekige driehoek ABC (LC = 90 graden) als gegeven is

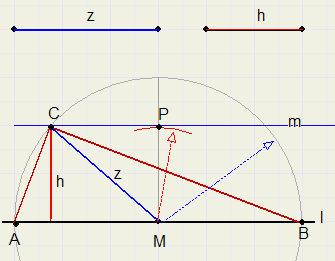
a. de lengte van de hoogtelijn uit C en de lengte van de zwaartelijn uit C

Lijnstuk z is zwaartelijn en h is hoogtelijn.
Teken lijn l met daarop punt M.
Cirkel z om vanuit M.
Construeer hoogtelijn op l en door M.
Pas h af op hoogtelijn vanuit M (MP = h).
Construeer lijn m door P en evenwijdig aan l.
Snijpunt m met cirkel is C.
ABC is de gevraagde driehoek.

LC staat op middellijn AB dus LC = 90 graden.
z is de straal van de cirkel door A,B en C

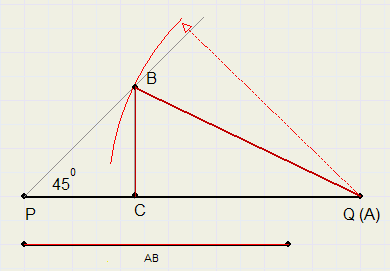
b. de schuine zijde AB en de som van de rechthoekszijden AB + BC

PQ = AC + BC.
Construeer bij P een hoek van 45 graden.
Cirkel AB om vanuit Q, snijpunt met zijde LP is B.
Laat loodlijn neer vanuit B op PQ. Snijpunt met PQ is C
Noem punt Q = A.
ABC is de gevraagde driehoek.

BC = PC, dus BC + AC = PQ.

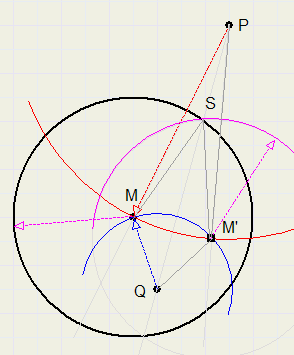
11.

Gebruik bij deze opgave alleen een passer.
Maak gebruik van de constructie bij opgave 1.

Gegeven zijn een cirkel met middelpunt M,
een punt P buiten- en een punt Q binnen de cirkel.
Construeer het snijpunt van de lijn l door P en Q met de cirkel.

Cirkel PM om vanuit P.
Cirkel QM on vanuit M.
Snijpunt cirkelbogen is M' (M gespiegeld om PQ)
Cirkel straal van gegeven cirkel om vanuit M'.
Snijpunt met gegeven cirkel is S.
S is het snijpunt van PQ met de cirkel.

PQ is middelloodlijn van MM'.
MS = M'S, dus S ligt op middelloodlijn PQ.

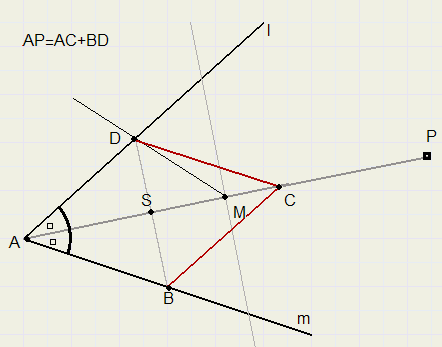
12.

Construeer een ruit als gegeven zijn
een scherpe hoek en de som van de diagonalen.

Gegeven zijn de lijnen l en m met hun snijpunt A.
Construeer deellijn van A en pas gegeven afstand AP af.
(AP = BD + AC, de som van de diagonalen)
Bepaal het midden M van AP.
Construeer bij M een hoek van 45 graden.
(LAMD = 45 graden)
Zijde van deze hoek snijdt l in D.
Laat vanuit D loodlijn neer op AP.
Loodlijn snijdt m in B.
Trek lijn door B evenwijdig aan AD, snijpunt met AP is C.
Trek lijn CD.
ABCD is de gevraagde ruit.

De diagonalen van een ruit zijn deellijnen van de hoekpunten,
staan loodrecht op elkaar en delen elkaar middendoor.
AS + SD = AS + SM = AM = PQ /2.
AS + SD = (AC + BD) / 2 .
PQ = AC + BD