constructies met Passer en Liniaal

Dit artikel beschrijft een aantal meetkundige basisconstructies met passer en liniaal.
Er komt geen gradenboog aan te pas.
De liniaal dient alleen voor het tekenen van rechte lijnen, er wordt geen gebruik gemaakt van afstanden
of schaalverdeling.
De passer dient voor het tekenen van cirkels en aftekenen van gelijke afstanden op rechte lijnen.

Inhoud

middelloodlijn
omgeschreven cirkel
loodlijn neerlaten
loodlijn oprichten
deellijn
ingeschreven cirkel
lijn evenwijdig en door punt
lijnstuk in gelijke delen verdelen
raaklijn aan cirkel
een hoek overzetten
hoeken van 30, 45, 60, 72 graden
driedeling van een hoek
de wortel uit a*b
lijnstuk a * b
lijnstuk a / b
regelmatige zeshoek
regelmatige negenhoek
opgaven

Middelloodlijn

De middelloodlijn is een van de belangrijkste lijnen in de vlakke meetkunde.
De middelloodlijn van lijnstuk AB wordt gevormd door alle punten die gelijke afstand hebben tot punten A en B
Gegeven zijn de punten A en B.
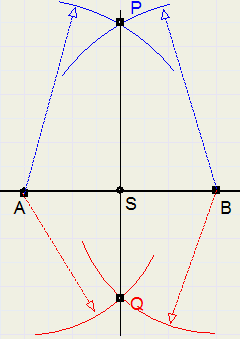
Construeer de lijn die loodrecht staat op AB en door het midden van AB gaat
    1. cirkel gelijke afstanden om vanuit punten A en B. Het snijpunt is P
    2. cirkel gelijke afstanden om vanuit punten A en B. Het snijpunt is Q
    3. lijn PQ is de middelloodlijn van AB
merk op
    S is het snijpunt van PQ met AB
    AS = BS
    AP = BP
    AQ = BQ
    LPAB = LPBA

De Omgeschreven Cirkel

Gegeven zijn 3 punten: A,B en C.
Construeer de cirkel door A, B en C
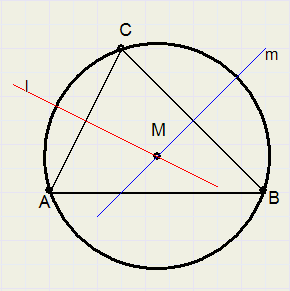
    1. construeer de middelloodlijn l van AC
    2. construer de middelloodlijn m van BC
    3. middelpunt M van de cirkel is het snijpunt van l en m
    4. teken cirkel vanuit M met straal MA = MB = MC
merk op
    constructie van middelloodlijnen niet getoond voor de duidelijkheid
    de middelloodlijnen van een driehoek gaan door 1 punt
    (de middelloodlijn van AB gaat door M)

Een Loodlijn neerlaten

Gegeven zijn een lijn l en punt P daarbuiten.
Construeer een lijn door P, die loodrecht staat op l.
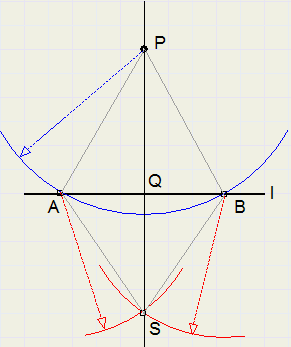
    1. trek cirkelboog vanuit P, A en B zijn snijpunten met l (zorg voor ruime afstand AB)
    2. trek gelijke cirkelbogen vanuit A en B, snijpunt cirkelbogen is S
    3. PS snijdt l in Q
    4. PQ is de loodlijn van P op l
merk op
    driehoeken PAQ en PBQ zijn congruent (gelijk), dus LPQA = LPQB = 90 graden.
    PQ is de afstand van P tot l (tevens de kortste afstand)

Een Loodlijn oprichten

Gegeven zijn een lijn l met daarop een punt P.
Construeer een lijn loodrecht op l en door P.

manier 1

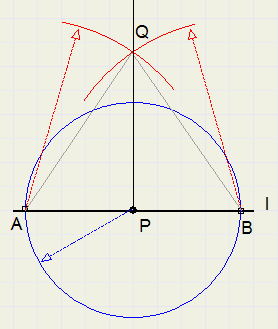
    1. trek cirkel vanuit P, A en B zijn snijpunten met l
    2. trek gelijke cirkelbogen vanuit A en B, snijpunt is Q
    3. PQ is de loodlijn op l, door P
merk op
    LAPQ = LBPQ = 90 graden, wegens congruente driehoeken APQ en BPQ

manier 2

Deze methode is geschikt als P het eindpunt is van een lijnstuk.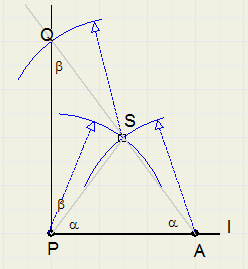
    1. kies een punt A op l. Zorg voor ruime afstand PA
    2. cirkel gelijke afstanden om vanuit A en P, snijpunt is S
    3. trek lijn door A en S
    4. verleng lijnstuk AS met SQ = AS
    5. PQ is de loodlijn op l door P
merk op
    in driehoek APS is PS = AS, dus LSPA = LSAP = a
    in driehoek PSQ is PS = SQ, dus LQPS = LPQS = b
    in driehoek APQ is 2a + 2b = 180 graden, zodat
    LAPQ = a + b = 90 graden

De Deellijn

De deellijn van een hoek verdeelt die hoek in twee gelijke hoeken.

Gegeven zijn de lijnen l en m met hun snijpunt P.
Construeer een lijn n, die de hoek tussen l en m in twee gelijke delen verdeelt..
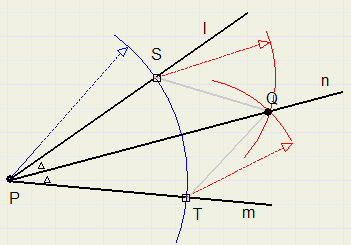
    1. trek cirkelboog vanuit P, snijpunten met l en m zijn S en T. Zorg voor ruime afstand PS
    2. trek gelijke cirkelbogen vanuit S en T, snijpunt is Q
    3. PQ is de deellijn van LP
merk op
    driehoeken PQS en PQT zijn congruent, zodat de hoeken bij P gelijk zijn.
    Elk punt op n heeft gelijke afstanden tot l en m (eveneens wegens congruente driehoeken)

De Ingeschreven cirkel

Gegeven is driehoek ABC.
Te construeren de cirkel waaraan AB, BC en AC raaklijnen zijn.
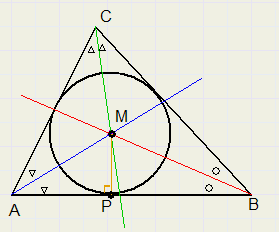
    1. construeer de deellijn van LA...........(constructie niet getoond)
    2. construeer de deellijn van LB...........(idem)
    3. M is het snijpunt van de deellijnen en tevens het middelpunt van de ingeschreven cirkel
    4. laat loodlijn MP neer op AB.
    5. MP is de straal van de ingeschreven cirkel
merk op
    alle punten op een deellijn liggen evenver van de zijden van die hoek
    zodoende ligt M evenver van AB, BC en AC
    De deellijnen van de hoeken van een driehoek gaan dus door één punt

Lijn evenwijdig en door Punt

Gegeven zijn een lijn l en een punt P daarbuiten.
Construeer een lijn (m) door P, evenwijdig aan l.

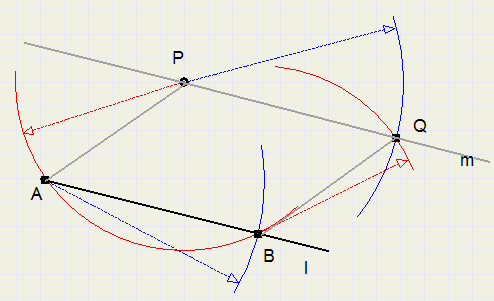
manier 1

    1. trek cirkelboog vanuit P, die l snijdt in twee punten (zorg dat punten ruim uit elkaar liggen)
    2. noem snijpunten A en B.
    3. teken cirkelboog vanuit P met straal AB
    4. teken cirkelboog vanuit B met straal AP
    5. Q is het snijpunt van bogen ..3) en ..4)
    6. trek lijn door P en Q, dit is de gevraagde lijn
merk op
    wegens PA = QB en AB = PQ is ABQP een parallellogram
    AB en PQ zijn daarom evenwijdige lijnen

manier 2

Dit is een snelle manier van evenwijdige verschuiving.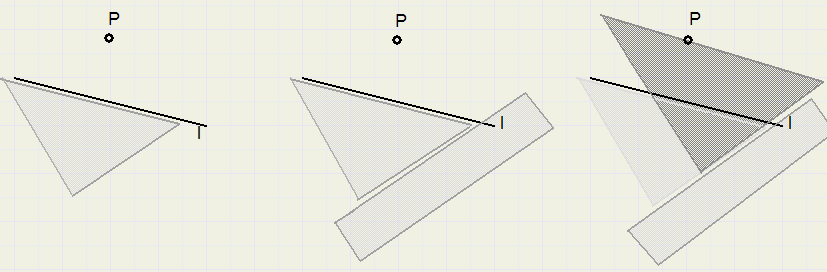
    1. leg een driehoek tegen lijn l
    2. plaats een liniaal tegen de driehoek
    3. verschuif de driehoek langs de liniaal, tot de zijde precies over punt P ligt

Lijnstuk in gelijke delen verdelen

Verdeel lijnstuk AB in vijf gelijke delen.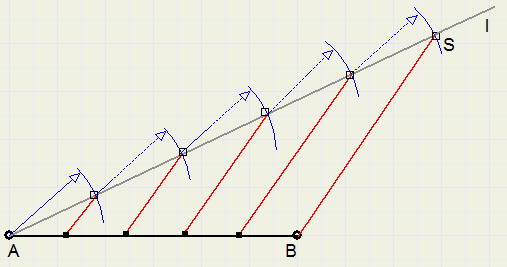
    1. trek hulplijn l door A
    2. zet vanuit A vijf gelijke stukken af op l, einde is punt S
    3. trek lijn BS
    4. trek lijnen evenwijdig aan BS, zie figuur
    5. deze lijnen verdelen AB in vijf gelijke stukken
merk op
    hier wordt de stelling toegepast:
    "evenwijdige lijnen verdelen snijdende lijnen in stukken met gelijke verhouding"
    Omdat de delen van l gelijk zijn, zijn de delen op AB dat ook

Raaklijn aan cirkel

Gegeven is een cirkel met middelpunt M en een punt P buiten de cirkel.
Construeer de raaklijn aan de cirkel die door P gaat.

manier 1

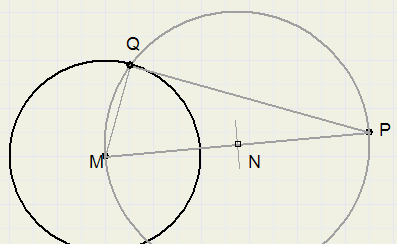
    1. trek PM
    2. bepaal midden N van PM (middelloodlijn constructie)
    3. trek cirkel, middelpunt N, straal MN
    4. Q is snijpunt cirkels
    5. trek raaklijn PQ
merk op
    LMQP = 90 graden, want staat op middellijn MP van cirkel N (zie "stelling van Thales")

manier 2

    1. trek lijn door PM. Snijpunten met cirkel zijn U en V
    2. neem afstand UV in de passer en cirkel om vanuit M (cirkel met dubbele straal ontstaat)
    3. cirkel afstand PM om vanuit P, snijpunt met grote cirkel is A.
    4. trek lijn MA, Q is snijpunt met oorspronkelijke cirkel
    4. trek raaklijn PQ
merk op
    PQ is de middelloodlijn van gelijkbenige driehoek PAM,
    dus PQ staat loodrecht op MQ
    (de raaklijn aan een cirkel staat loodrecht op de straal naar het raakpunt)

Een hoek overzetten

Gegeven zijn de lijnen l en m, hun snijpunt A en een punt P op lijn p.
Construeer een lijn s door P zo, dat de hoek tussen s en p even groot is als de hoek bij A.
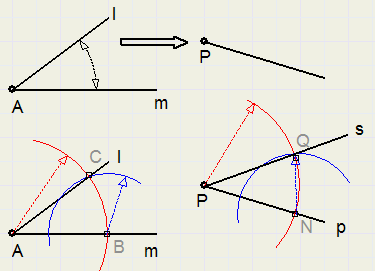
    1. trek een cirkelboog vanuit A. (neem ruime straal) Snijpunt met l is C, snijpunt met m is B
    2. neem AB in passer en cirkel om vanuit P. (snijpunt met p is N, zie figuur)
    3. neem BC in de passer en cirkel om vanuit N. Snijpunt cirkelbogen is Q.
    4. trek lijn s door P en Q
merk op
    driehoeken ABC en PNQ zijn congruent, dus de hoeken bij A en P zijn gelijk.

Hoeken van 30, 45, 60, 72 graden

We beperken ons in dit artikel tot hoeken van hele graden.
Niet elke hoek blijkt dan construeerbaar.
Een artikel over de construeerbaarheid van hele hoeken vind je hier:
https://www.pandd.nl/downloads/constrhoeken.pdf

Niet construeerbaar zijn hoeken van 1, 2, 4, 5 , 10 ..........graden.
Wel construeerbaar zijn alle hoeken die een veelvoud zijn van 3 graden.

Gegeven is steeds een punt A op lijn l.
Construeer de lijn door A, die met l de gevraagde hoek maakt.

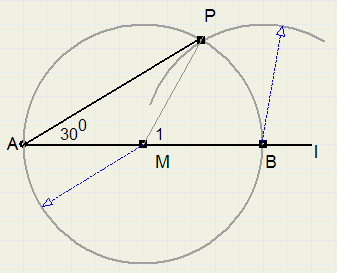
30 graden

    1. Kies punt M op l, niet te dicht bij A
    2. trek cirkel met middelpunt M en straal MA
    3. cirkel snijdt l ook in B
    4. cirkel afstand MA om vanuit B, snijpunt cirkels is P
    5. LPAB = 30 graden
merk op
    driehoek MBP is gelijkzijdig, dus LM1 = 60 graden.
    LA staat op cirkelboog van 60 graden, dus is zelf 30 graden (stelling van Thales)

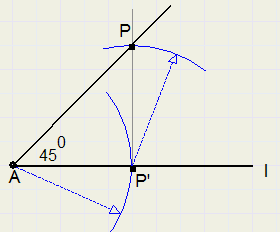
45 graden

    1. kies punt P', niet te dicht bij A
    2. richt loodlijn op vanuit P'
    3. cirkel afstand AP' om vanuit P', snijpunt cirkel met loodlijn is P
    4. LPAP' = 45 graden
merk op
    driehoek PAP' is rechthoekig en gelijkbenig, dus de scherpe hoeken zijn 45 graden

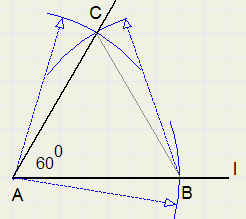
60 graden

    1. kies punt B op l, niet te dicht bij A
    2. cirkel afstand AB om vanuit A en vanuit B
    3. C is snijpunt cirkelbogen
    4. LCAB = 60 graden
merk op
    driehoek ABC is gelijkzijdig, dus alle hoeken zijn 60 graden

72 graden

Bij deze constructie is het uitgangspunt een regelmatige vijfhoek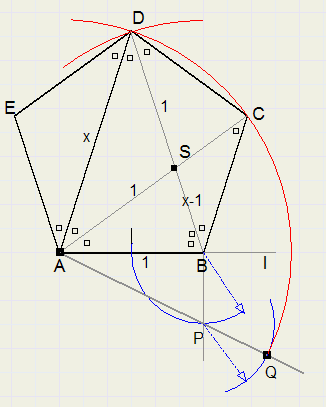
    1. kies punt B op l. (Stel AB = 1)
    2. richt loodlijn op in punt B
    3. bepaal midden van AB (middelloodlijn)
    4. pas deze afstand (1/2) af op loodlijn. BP = 1/2
    5. trek lijn AP
    6. verleng AP met 1/2. ( AQ = AP + 1/2)
    7. cirkel AQ om vanuit A en B, snijpunt is D
    8. LDAB = 72 graden
merk op
    In de figuur staat elk merkje (vierkantje) voor 36 graden.
    AS is deellijn. AB = AS = SD (gelijkbenige driehoeken)
    Stel AB = 1 en AD = x. Deellijnstelling:
    x : 1 = 1 : (x-1) of:
    x2 - x - 1 = 0
    x = 
    1
    2
     + 
    1
    2
     
    \5
     = AQ

Driedeling van een hoek

Eerder spraken we af geen liniaal met schaalverdeling te gebruiken.
Met dat gereedschap is deze constructie niet mogelijk.
Maar met een kleine verandering: een liniaal met slechts twee streepjes, kan het wel.
We delen LBAC in drie gelijke delen:
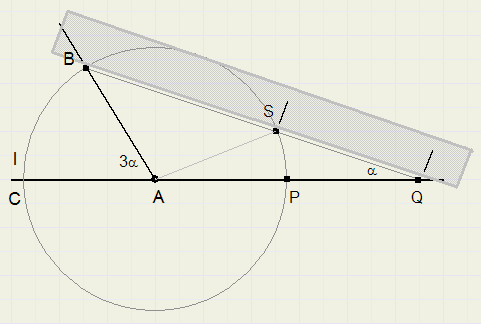
    1. cirkel afstand CA om vanuit A.
    2. verleng lijnstuk CA
    3. breng op liniaal 2 streepjes aan met afstand CA
    4. leg liniaal langs punt B en schuif zodanig dat de merkstreepjes bij S en op de verlengde lijn CA liggen
    5. LBQC = 1/3 * LBAC
merk op
    Stel LBAC = 3a en LBQC = x
    vlg. stelling van Thales is dan x = 1/2 boog BC - 1/2 boog PS = 1/2 (3a - x)
    2x = 3a - x
    x = a

De wortel uit a*b

Gegeven zijn 2 lijnstukken met lengtes a en b.
Construeer een lijnstuk met lengte wortel uit ab
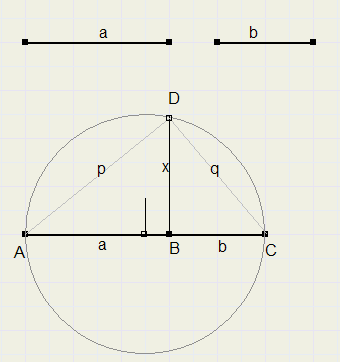
    1. pas lengtes AB = a en BC = b af op een lijn
    2. beschouw AC als middellijn van een cirkel, teken de cirkel
    3. richt loodlijn op AC op, door B
    4. loodlijn snijdt cirkel in D
    5. BD is de lengte : wortel uit ab
merk op
    stel AD = p , CD = q , BD = x
    wegens rechthoek is
    a2 + x2 = p2
    b2 + x2 = q2
    p2 + q2 = (a+b)2
    combinerend:
    a2 + x2 + b2 + x2 = (a+b)2
    a2 + 2x2 + b2 = a2 + 2ab + b2
    x2 = ab

Lijnstuk a * b

Gegeven zijn lijnstukken met lengtes a en b en ook een lijnstuk met lengte 1.
(zonder de 1 zouden we niet weten of het product groter of kleiner dan bv a zou worden)
De constructie maakt gebruik van de stelling dat evenwijdige lijnen snijdende lijnen
verdelen in stukken met gelijke verhouding.
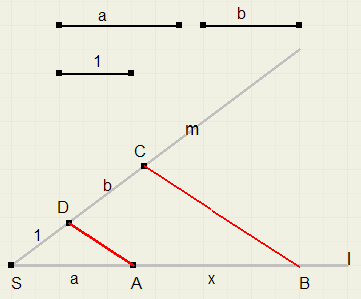
    1. teken snijdende lijnen l en m (neem hoek tussen 45 en 90 graden)
    2. pas afstanden 1 (SD) en b (DC) af op m
    3. pas a (SA) af op l
    4. trek lijn AD
    5. trek lijn BC evenwijdig aan AD
    6. AB = a*b
merk op
    stel AB = x
    wegens evenwijdigheid AD en BC geldt:
    SA : SD = AB : DC
    a : 1 = x : b
    x = ab

Lijnstuk a / b

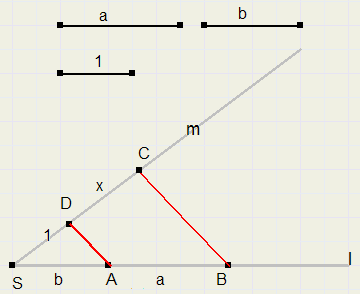
    1. teken snijdende lijnen l en m
    2. pas afstand 1 af op m
    3. pas afstand b (SA) en afstand a (AB) af op l
    4. trek lijn AD
    5. trek lijn BC evenwijdig aan AD
    6. DC = a/b
merk op:
    1 : b = x : a
    x = a/b

Regelmatige zeshoek

Uitgaande van de lengte AB van een zijde construeren we een regelmatige zeshoek.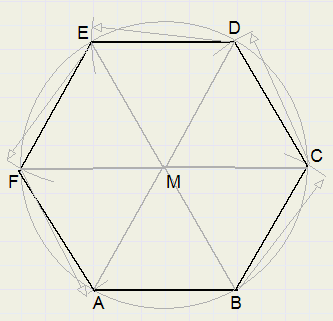
    1. construeer gelijkzijdige driehoek ABM (omcirkelen AB vanuit A en B)
    2. cirkel MA om vanuit M
    3. pas afstanden MA af op de cirkel, snijpunten zijn B, C, D, E, F
    4. trek lijnen BC, CD, DE, EF, FA
merk op
    alle driehoeken (MAB, MBC ...enz) zijn gelijkzijdig, dus hoeken zijn 60 graden
    de zes middelpuntshoeken bij M zijn samen 360 graden

Regelmatige negenhoek

Deze constructie is eigenlijk niet mogelijk, omdat er hoeken van 20 of 40 graden geconstrueerd moeten worden.
Maar door 2 streepjes op de liniaal toe te staan kan een hoek van 60 graden in drieën worden verdeeld,
zodat het toch lukt.
We construeren de negenhoek uitgaande van de gegeven zijde AB
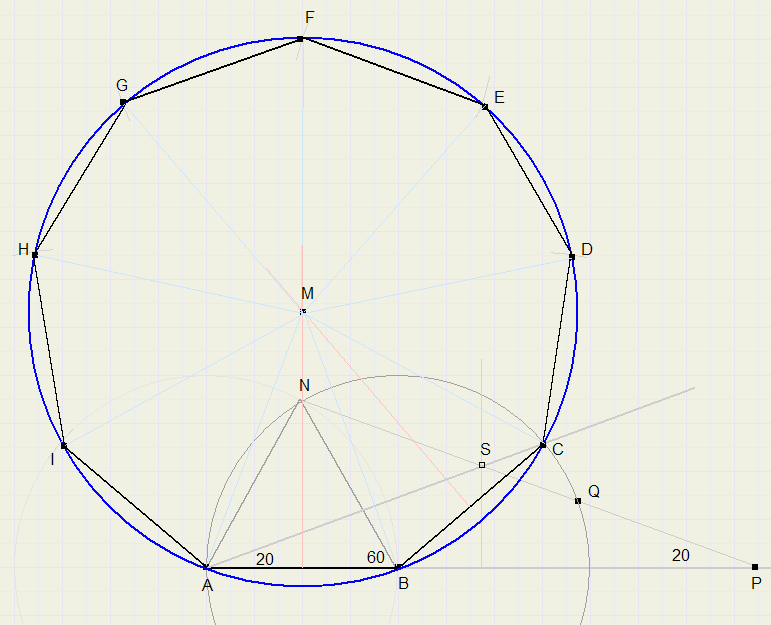
    1. kies zijde AB (bv 4 cm)
    2. verleng AB
    3. construeer gelijkzijdige driehoek NAB
    4. cirkel BN om vanuit B
    5. breng op liniaal 2 merkstreepjes aan met afstand AB
    6. leg liniaal langs punt N, snijpunt met verlengde AB is punt P, snijpunt met cirkel is Q
    7. verschuif liniaal zodat PQ = AB (streepjes vallen op P en Q)
    8. LNPA = 20 graden. We spiegelen nu P naar A
    9. construeer middelloodlijn van AP, snijpunt met NP is S
    10. trek lijn door A en S, LSAB = 20 graden
    11. verleng AS, C is snijpunt met cirkel om B met straal AB
    12. construeer de middelloodlijnen van AB en BC, snijpunt is M
    13. trek cirkel vanuit M met straal MB
    14. pas afstanden AB (= BC) af op de cirkel, noem punten D, E, F, G, H, I
    15. ABCDEFGHI is een regelmatige negenhoek
merk op
    een regelmatige negenhoek verdeelt de omgeschreven cirkel in bogen van 40 graden
    1...8 construeert LCAB = 20 graden (staat op cirkelboog 40 graden)
    Middelpunt M is snijpunt middelloodlijnen van 2 zijden

Andere constructie 40 graden hoek

Fedde Reeskamp bedacht deze fraaie methode om een hoek van 40 graden te construeren: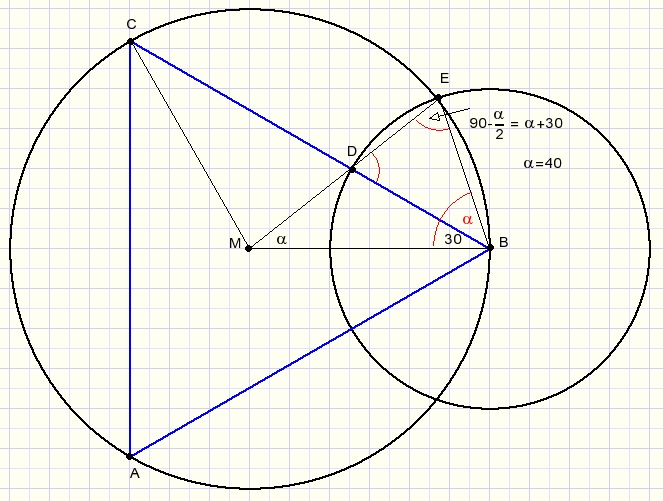



Hij gaat uit van een gelijkzijdige driehoek (ABC) met zijn omgeschreven cirkel.
Vanuit punt B wordt een cirkel getekend waarbij punten M, D en E op één lijn liggen.
De straal van deze cirkel moet experimenteel worden benaderd.
Constructie is niet mogelijk.
Zie het plaatje hierboven voor het bewijs.
BE is koorde van een regelmatige 9 hoek.

Op het eerste gezicht lijkt de verhouding tussen de stralen van de cirkels 3:2 te zijn.
Maar dat is niet juist.
Als die verhouding wordt gekozen dan wordt de hoek 38,94 graden.