programming: mod & div operators

Delphi programming: mod & div operators

Inleiding

Dit artikel beschrijft enkele toepassingen van de mod en div operators in de programmeertaal Delphi.

Computers kunnen alleen werken met getallen.
Alleen problemen die in getallen zijn uit te drukken kunnen met computers worden opgelost.
In het dagelijks leven gebruiken we getallen op vier verschillende manieren

soort	voorbeeld
hoeveelheid	kilogram, graden, meters, seconden
factor	15%, de helft
rangorde	4 sterren camping, 2e van links, huisnummer
code	pincode, bus 167, ASCII code

Telwerken

Rekenen begint met tellen. Hieronder staat een eenvoudig telwerkje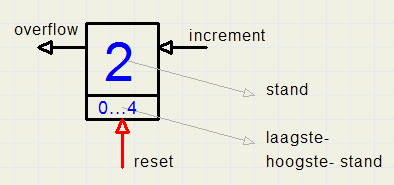

Het is niet van belang hoe het werkt, dat kan zijn mechanisch met tandwielen,
elektronisch of elektro-mechanisch met relais.
Het “reset” signaal forceert de teller in de eerste stand: de “0”.
Increment (verhoog) zet de teller in de volgende stand.
Een “increment” bij stand 4, de hoogste, zet de teller in stand “0” en heeft een “overflow” signaal tot gevolg:
de teller gaat “over de kop”.
In de digitale techniek heet zo'n overflow signaal een “carry”.

Stel nu, dat we na “reset” N increments geven.
Onderstaande tabel toont de tellerstand T afhankelijk van de waarde van N.

N	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
T	0	1	2	3	4	0	1	2	3	4	0	1	2	3	4

Om T als functie van N uit te drukken is een aparte notatie nodig, we schrijven

T = N mod 5 We zien, dat T de rest is bij deling van N door 5.
mod is een operator, net als + - *

Uit de tabel hierboven lezen we af : 14 mod 5 = 4
Als we een modulo 44 teller hebben (hoogste stand dus 43) en we verhogen die teller 1208 maal dan zal de stand T zijn

T = 1208 mod 44 Om in Delphi 1208 mod 44 te berekenen tikken we simpelweg in: T := 1208 mod 44.

Met de rekenmachine gaan we als volgt te werk om T te berekenen:
1208 : 44 = 27,4545... haal nu de cijfers voor de komma weg en vermenigvuldig 0,4545... * 44 = 20
let op: soms is een hele kleine afronding nodig om een geheel getal te krijgen.

Het aantal keren dat een teller over de kop gaat noemen we even C (aantal carries).
Notatie:

C = N div 5 levert het aantal carries van een modulo5 teller bij N increments.
We zien, dat C het aantal 5 tallen geeft, omlaag afgerond.

Om in Delphi C = 1208 div 44 te berekenen tikken we: C := 1208 div 44
Met de rekenmachine :
1208 : 44 = 27,4545... laat cijfers achter de komma weg, zodat 1208 div 44 = 27.

div is ook een operator, zoals + - * of mod

Afronden

In een tekenprogramma werken we in een paintbox met ruitjes van 20 * 20 pixels.
Elke MouseMove levert een X (en ook Y) waarde.
X div 20 levert dan het aantal gehele ruitjes links van de cursor, zodat
(X div 20) * 20 .....de X pixelpositie geeft, omlaag afgerond op veelvouden van 20

Willen we X afronden op het dichtstbijgelegen veelvoud van 20, dan berekenen we

((X + 10) div 20) * 20.......................{ 10 = 20 div 2 } Voor afronding omhoog wordt dat

((X + 19) div 20) * 20.......................{19 = 20 - 1}

Twee dimensionale tabellen

De velden zijn genummerd 0..23.
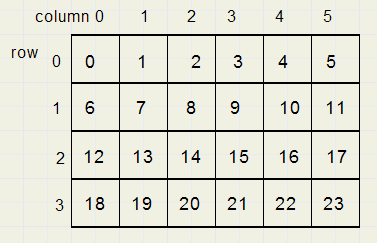
Noemen we N het nummer van een veld, dan is N = kolom + rij * 6.
In de kolom herkennen we een modulo 6 teller. ( 23 mod 6 = 5)
Bij bekende waarde van N kan de kolom en de rij worden berekend volgens

Het computergeheugen is een eendimensionale tabel van bytes.
Bij tweedimensionale tabellen moet dus steeds een kleine berekening worden gemaakt om de lokatie te vinden.
In Delphi zijn de velden van een tweedimensiaal array zo opgeslagen:
(0,1,2,3,... liggen op volgorde in de bytes van het geheugen)

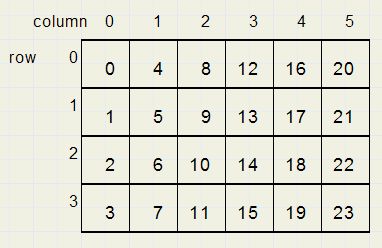
We definiëren bovenstaand array zowel één- als tweedimensionaal

var A1 : array[0..23] of byte;
    A2 : array[0..5,0..3] of byte absolute A1; // A1,A2 gebruiken zelfde geheugenruimte

Zodoende is A1[9] hetzelfde veld als A2[2,1]

Algemeen :
Inplaats van A2[ col, row] kunnen we ook nemen A1[col*4 + row].

A1[ i + 4] adresseert dus 1 veld naar rechts, A1[ i – 3] adresseert het veld linksonder.
Met deze tactiek kan bij het programmeren van bordspelletjes flinke tijdwinst worden behaald.
Immers, de velden kunnen met simpele + en – bewerkingen horizontaal, vertikaal
of diagonaalsgewijs worden doorlopen.

Plaats op het scherm

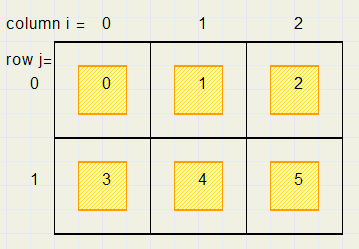
Op het plaatje hierboven is elk zwart omlijnd vakje 100 * 100 pixels op het beeldscherm.
Een Mousemove levert de coördinaten (x,y) van de cursor op, zodat

Elke veld heeft een oranje gebiedje en we willen testen of de pointer zich daarin bevindt
We programmeren:

var orange : boolean;
 x100,y100 : word;
........... 
x100 := x mod 100;
y100 := y mod 100;
orange := (X100 > 25) and (x100 < 75) and (y100 > 25) and (y100 < 75);

Sudoku

De cijferpuzzel Sudoku telt kolommen 1..9, rijen 1..9 en groepen 1..9.
Zie plaatje.

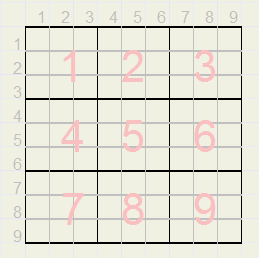
Merk op, dat de telling loopt van 1..9. Dat is niet handig, zodat we rekenen met (i-1)
(j-1) voor kolom i en rij j......{dus 0..8 ipv 1..9}
Gegeven kolom i en rij j willen we berekenen in welke groep het veld zit. Dat kan zo:

function IJtoGroupNr(i,j : byte) : byte;
//return group Nr of field [i,j]
var x,y : byte;
begin
 x := (i-1) div 3;
 y := (j-1) div 3;
 result := x + 3*y + 1;
end;

Tellers koppelen

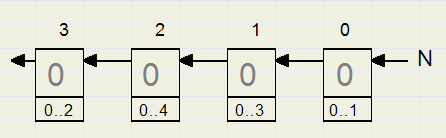
Hierboven zijn vier tellers in serie gekoppeld.
Teller T0 is een modulo 2, T1 een modulo 4, T2 een modulo 5 en teller T3 telt modulo 3.
De gehele teller is te beschouwen als een modulo (2 * 4 * 5 * 3) = modulo 120 teller.
Na 120 verhogingen is de stand weer 0 0 0 0 en er heeft 1 carry van teller 3 plaatsgevonden.

Stel dat N = 68. Wat zal dan de stand T0..T3 zijn van de tellers afzonderlijk?

68 mod 2 = 0, dat is dus T0 = 0
86 div 2 = 43, dat is het aantal carries van teller 0

Teller 1 ontvangt 43 increments zodat T1 = 43 mod 4 = 3
43 div 4 = 10, het aantal carries uit T1, zodat

De tellers staan dus op 2 0 3 0 (geschreven van links naar rechts)
Nu zal de lezer zich afvragen wat het nut is van dit gereken.
Ziehier:
In een pannenkoekenhuis kunnen de volgende keuzes worden gemaakt bij de bestelling:

soort meel	wit (0) of bruin (1)	teller 0
grootte	klein (0) middel(1) groot(2) extra groot (3).	teller 1
soort	naturel (0) appel (1) spek (2) kaas (3) banaan (4)	teller 2
beleg	suiker (0) stroop (1) jam (2)	teller 3

We willen een bestelling zodanig coderen dat een minimum aan geheugenruimte nodig is.
Merk op, dat elke keuze overeenkomt met een tellertje in de figuur hiervoor.

De eerder gevonden tellerstand 2 0 3 0 komt overeen met de pannenkoekenkeuze

wit meel.....extra groot.....naturel......jam N is de code hiervoor: 68.

Hoe codeer je nu de keuze bruin(1), groot(2), appel(1), suiker(0) ?

Dat is dus tellerstand 0 1 2 1, gevraagd is N te berekenen.
T2 is 1 * verhoogd, daarvoor zijn nodig 2 * 4 increments voor T0, want T0T1 vormen samen een modulo 8 teller.
Dus N = 8 voorlopig.
T1 is 2 maal verhoogd, daarvoor zijn 2 * 2 increments van T0 nodig, die immers een modulo 2 teller is,
dus N = 8 + 4 = 12.
T0 is 1 maal verhoogd, dus N = 12 + 1 = 13, wat de code is voor deze pannenkoekenkeuze.
Elke teller levert dus zijn stand * (modulus voorgaande tellers samen) op voor N.

Talstelsels

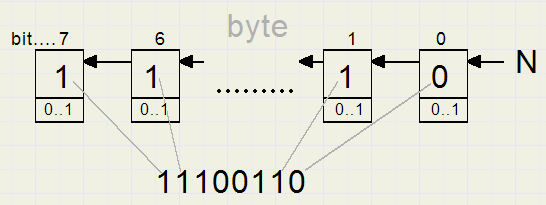
Hierboven staat een telwerk dat we als “byte” herkennen.
Een tellertje heet een bit en onderaan de figuur staat de verkorte notatie zoals we die kennen bij talstelsels.

De modulus is 2^8 = 256
Als elke teller van het type modulo 10 zou zijn, dan was het getal N niet in het twee- maar in het 10 tallig stelsel weergegeven.

Omzetten van 2- naar 10 tallig stelsel doen we door N ook aan modulo 10 tellers te koppelen.
N mod 10 is dan de stand van T0, N div 10 is het aantal carries uit T0, dus increments van T1.

Het programma hieronder zet een (positieve) integer uit het 2 tallig stelsel om in een string

procedure setN(nn : cardinal; t : byte); //displays getal -nn- in  t  tallig stelsel
const digitconvert = '0123456789abcdef';
var s : string;
    m : byte;
begin
 if nn = 0 then begin
                 form1.edit2.text := '0';
                 exit;
                end;
 s := '';
 repeat
  m := nn mod t;
  nn := nn div t;
  insert(digitconvert[m+1],s,1);
 until nn = 0;
 form1.edit2.text := s;
end;

Bit fields

mod en div zijn relatief trage bewerkingen, omdat het een deling betreft.
Voor de snelheid is het daarom beter om ze te vermijden.
Dat kan, als de modulus een veelvoud is van 2, dus een aantal bits betreft.

N div 2 is hetzelfde als N shr 1, een right shift.

Algemeen : N div (2 ^ i) = N shr i

Ook is N mod (2 ^ i) = N and (2^ i – 1)

In plaats van N mod 8 is de berekening N and $7 heel wat sneller bij gelijk antwoord.
(het hexadecimale $ teken is hier niet echt nodig, maar geeft wel een bit-georienteerde bewerking aan)

Stel dat we een spel programmeren waarbij een tabel nodig is van 1000 bij 1000 bits
met daarbij drie procedures/functies.

Hoe pakken we dit aan?
We stoppen simpelweg alle bits in een ééndimensionaal array van bytes.
Dat array moet dus 1000 * 1000 / 8 = 125000 bytes bevatten.

Var BitArray : array[0..124999] of byte;

procedure setbit(i,j : word);
var AbitNr : integer;
   byteNr,bitNr : byte;
begin
 ABitNr := i + 1000 * j  ; // bitnumber in array,geteld 0..999 in rij 1, 1000..1999 in rij 2 
 ByteNr := ABitNr shr 3; //div 8 = index in byte array
 bitNr := AbitNr and $7; //bitnumber in byte
 BitArray[byteNr] := BitArray[byteNr] or (1 shl bitNr);
end; 
 
procedure clearbit(i,j : word);
var AbitNr : integer;
      byteNr,bitNr : byte;
begin
 ABitNr := i + 1000 * j  ; // bitnumber in array , geteld 0..999 in rij 1,  1000..1999 in rij 2 
 ByteNr := ABitNr shr 3; //div 8 = index in byte array
 bitNr := AbitNr and $7; //bitnumber in byte
 BitArray[byteNr] := BitArray[byteNr] and ($ff xor (1 shl bitNr));
end; 
 
function  testbit(i,j : word) : byte;
var AbitNr : integer;
      byteNr,bitNr : byte;
begin
 ABitNr := i + 1000 * j  ; // bitnumber in array , geteld 0..999 in rij 1,  1000..1999 in rij 2 
 ByteNr := ABitNr shr 3; //div 8 = index in byte array
 bitNr := AbitNr and $7; //bitnumber in byte
 result := (BitArray[byteNr] shr bitnr) and $1;
end;

De volgende 200 priemgetallen

Elk -niet priem- getal is te schrijven als een uniek product van priemgetallen.
Priemgetallen spelen een belangrijke rol bij codes.
Voor dit artikel programmeerde ik een programmaatje dat steeds de volgende 200 priemgetallen berekent
en die netjes weergeeft in een paintbox in 20 rijtjes van 10.

Om overbodig werk te vermijden zijn de volgende trucs toegepast:

waarbij m = 5,7,11,13,17,19,23,25,29.....dus steeds afwisselend 2 of 4 ophoogt Opmerking:
1.
6K + 2 kan geen priemgetal zijn, want is deelbaar door 2
6K+3 is deelbaar door 3, 6K + 4 is weer deelbaar door 2.
dus alleen 6K-1 (of 6K+5) en 6K+1 kunnen mogelijk een priemgetal zijn.

2.
Een getal P is deelbaar door m als geldt P mod m = 0
Stel eens, dat P = 63 en m = 7. Dan geldt: 63 div 7 = 9 en 63 mod 7 = 0 ,
geen priemgetal dus, want P is een veelvoud van 7.
Stel eens, dat P = 67, we delen achtereenvolgens door 3,5,7,11,13...
67 div 7 = 9 en 67 div 11 = 6, maar.....6 < 11 , het antwoord is voor het eerst kleiner
dan het getal waardoor we delen.
Nu kunnen we concluderen dat het getal priem is, want een factor hadden we al eerder moeten vinden.

Het programma, met verwijzing naar het hele project, is [hier] te vinden

3.
In het programma komen twee labels en goto statements voor.
Dat is sommigen een gruwel, maar hier erg handig omdat er twee lussen zijn die elkaar kruisen.
Ik houd mij aanbevolen voor een aanpak volgens de conventies van het “gestructureerd programmeren”.

GGD berekenen

De grootste gemeenschappelijke deler van twee getallen laat zich het eenvoudigst berekenen
met het “Theorema van Euclides”.
In het kort komt dat neer op.......GGD(A,B) = GGD(A-B,B).
We berekenen als voorbeeld

Het onderstaande programmaatje berekent de GGD van getallen A en B
door herhaald toepassen van het 'Theorema van Euclides'.

function GGD(A,B : cardinal) : cardinal;
var r : cardinal;
begin
   repeat
     r := A mod B;
     A := B;
     B := r;
   until r := 0;
   result := A;
end;

En hiermee besluit ik dit artikel.