

 |
 |
Priemgetallen Generator |  |
 |
Inleiding
Priemgetallen zijn de natuurlijke getallen groter dan 1, die alleen door 1 en zichzelf deelbaar zijn.Van een priemhoeveelheid blikjes kunnen geen meerdere gelijke stapeltjes worden gemaakt.
De eerste 10 priemgetallen zijn: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
Elk getal kan slechts op ťťn unieke manier in priemfactoren worden ontbonden, zodat priemgetallen
kunnen worden opgevat als de bouwstenen van alle getallen.
Priemgetallen spelen een belangrijke rol in de wiskunde, o.a. bij het coderen van geheime berichten,
wat nodig is bij elektronisch betalingsverkeer.
Dit artikel beschrijft hoe het programma "priem200" priemgetallen berekent.
Theorie
Om te onderzoeken of een getal "priem" is, moet het door alle priemgetallen kleiner dan zichzelf worden gedeeld.Het quotient van zo'n deling mag nooit een geheel getal zijn, want dat betekent dat het getal een veelvoud
van een priemgetal is.
We kunnen ook zeggen: de deling mag nooit uitkomen, er moet altijd een rest zijn.
Computers kennen de bewerking mod, te vergelijken met : of / , de operator voor delen.
De bewerking P mod d levert de rest bij deling van het getal P door d.
Is deze uitkomst 0, dan is P geen priemgetal.
Stel dat we willen onderzoeken of 229 een priemgetal is.
We kunnen dan 229 delen door d = 2, 3, 4, 5..................., 228 en als steeds geldt dat 229 mod d = 0
dan kunnen we concluderen dat P een priemgetal is.
We doen dan echter teveel werk.
Priemgetallen groter dan 2 kunnen nooit even zijn, want dan zijn ze een veelvoud van 2.
P kunnen we dus (vanaf 3) steeds met 2 ophogen.
De deler d kan dan deze rij waarden aannemen: 3, 5, 7, 9, .......
Maar het kan nog iets beter, bekijk daarvoor de priemgetallen boven de 5:
.......7, 11, 13, 17, 19, 23, 29, 31, ...............we zien nooit dat d 2 maal achter elkaar met 2 verhoogt.
De reden is dat een priemgetal boven de 6 de vorm heeft van 6K+1 of 6K+5, waarbij K = 1,2,3,4......
ga maar na:
-
- 6K is deelbaar door 6
- 6K + 2 is deelbaar door 2
- 6k + 3 is deelbaar door 3
- 6K+4 is deelbaar door 2
......5, 7, 11, 13, 17, 19, 23, 25, 29...............steeds afwisselend 2 of 4 erbij.
Maar er is nog een versnelling mogelijk.
Computers maken onderscheid tussen gehele getallen en kommagetallen.
De operator voor delen met kommagetallen is '/ '.
Voor delingen met gehele getallen wordt (in de taal Delphi) de operator div gebruikt.
Bij zo'n deling worden dus in het quotient de cijfers achter de komma weggelaten.
Nog steeds onderzoeken we of 229 een priemgetal is.
-
1).........229 div 13 = 17..........de volgende deler is 17
2).........229 div 17 = 13
In regel 2) is het quotient kleiner dan de deler.
Dat betekent dat het geen zin heeft om d te verhogen en opnieuw 229 te delen,
want als 229 een (priem) factor bevatte dan waren we die al tegengekomen.
Ga maar na: als P = a.b waarbij a en b priemgetallen zijn dan geldt
-
P mod a = 0
P mod b = 0
P div a = b
P div b = a.......deze deling is overbodig als a < b
Zodra geldt dat (P div d) < d, dan kunnen we het delen staken.
Hieronder staat de flowchart van de procedure die, beginnend bij de waarde van P,
de volgende 200 priemgetallen berekent.
Flowchart
Hierin is-
P : het te onderzoeken getal
ip : de waarde waarmee P wordt verhoogd, dus afwisselend 2 en 4
d : de deler van P
id : de waarde waarmee d wordt verhoogd, dus afwisselend 2 en 4
n : het nummer van het priemgetal op het scherm, van 0..199
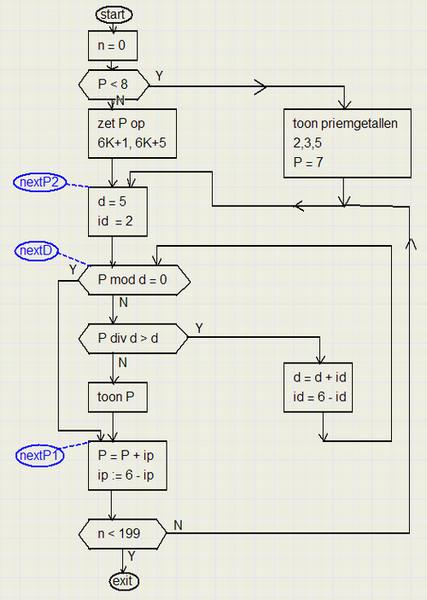
| rechthoeken | functie-boxen: hier worden handelingen verricht |
| dropvormen | beslissings-boxen: hier wordt een test gedaan afhankelijk van de uitslag (Y-yes, N-no) wordt een ander deel van het programma doorlopen |
| ellipsen | label: een plaats waar naartoe kan worden gesprongen |
Programma
Download het programma door op het "bliksem" icoon te klikken bovenaan deze pagina.Er is geen installatieprocedure, kopieer "priem200.exe" naar een map naar keuze.
GeÔnteresseerd in het gehele Delphi-7 project met de sourcecode? Klik dan [hier ]


