Meetkunde examen MULO - B 1931

Hieronder tref je aan het eindexamen meetkunde van de MULO-B in 1931.
Tijdsduur is 1,5 uur.
Bij de vraagstukken moet worden bedacht dat geen gebruik werd gemaakt van rekenmachines.

1.
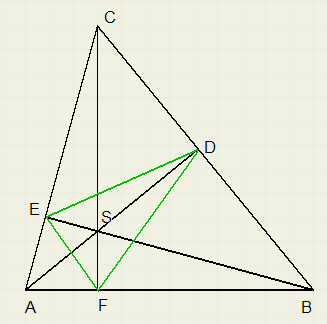
Men laat in DABC de hoogtelijnen AD, BE en CF neer op de zijden.
Uit D laat men een loodlijn neer op AB, die , verlengd, het verlengde van EF in G snijdt en uit D een loodlijn
op AC, die, verlengd, het verlengde van FE snijdt in H.

Bewijs dat GH gelijk is aan de omtrek van DDEF.

Zie figuur 1 hieronder:
DDEF is de zg. "voetpuntsdriehoek".
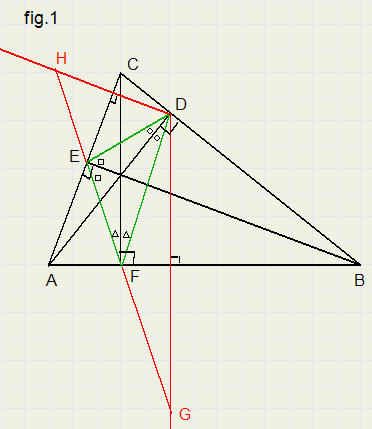
Een stelling luidt:
    "De hoogtelijnen van een driehoek zijn de deellijnen van de voetpuntsdriehoek".
Na het gehele examen zal ik deze stellling bewijzen.
Zonder gebruikmaking van deze eigenschap zou de opgave zeer lastig zijn.

In figuur 1 zijn dus de gelijkgemerkte hoeken gelijk.

Daarom is ook: LCED = LAEF.........en omdat ...........LAEF = LHEC is
LCED = LHEC.
daarom is

HE = ED.................{in een driehoek liggen tegenover gelijke hoeken gelijke zijden}

Op eenzelfde wijze kan worden vastgesteld dat GF = FD, zodat HG de omtrek is van DDEF

2.
Construeer (passer en liniaal) een driehoek, waarvan gegeven zijn:
een zijde, de hoogtelijn op die zijde, en de hoek die de beide andere hoogtelijnen met elkaar maken.

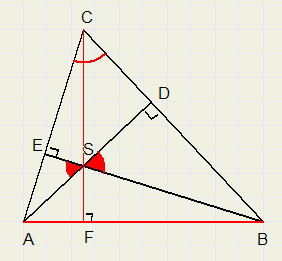
Eerst een oriënterend plaatje tekenen.
De gegeven zijden en hoek zijn rood gekleurd.
Nu is LC gelijk aan de hoek tussen hoogtelijnen AD en BE.
Beschouw daarvoor DBSD en DBEC.
Zowel LC als LBSD zijn, aangevuld met LSBD, gelijk aan 90°

De opgave verandert hiermee in:
construeer een driehoek waarvan gegeven zijn de basis, hoogtelijn op die basis en de tophoek.
Dat ziet er een stuk prettiger uit.
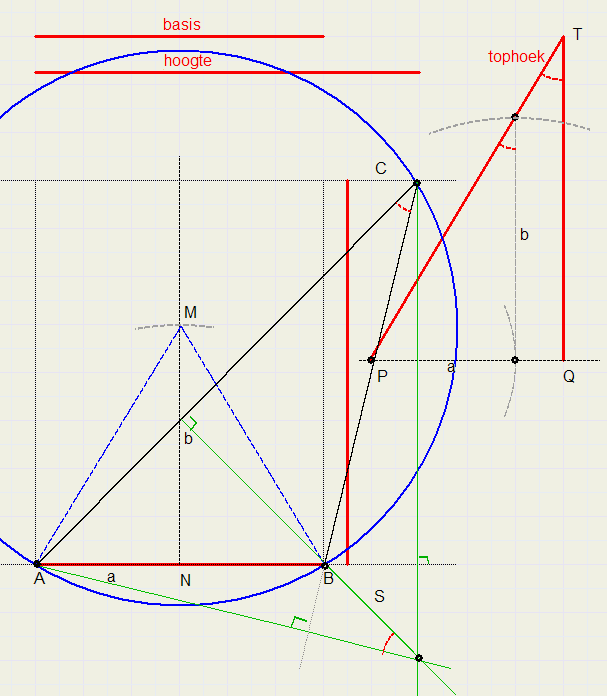
in de figuur hieronder zijn basis, hoogte en tophoek gegeven (getekend in rood).
De constructie verloopt als volgt:
    - teken een lijn met daarop de basis AB van de driehoek
    - construeer middelloodlijn op AB
    - neem een punt P op een van de benen van LT
    - laat loodlijn PQ neer
    - zet afstand a (AN) af op PQ
    - richt loodlijn b op, zie figuur
    - pas b af op middelloodlijn van AB ( = MN)
    - trek cirkel met middelpunt M door A en B
    - trek lijn evenwijdig aan AB op afstand h (= hoogte van de driehoek)
    - Top C is snijpunt van deze lijn met de cirkel
Uitleg:
boog AB = 2 * LT, zodat
LC = LT..........................{vlg. stelling van Thales}

Merk op , dat het snijpunt S van de hoogtelijnen (groen getekend), buiten de driehoek valt omdat LB stomp is.

Elementaire constructies van een middelloodlijn of loodlijn zijn hier niet getekend om een chaotische tekening te vermijden.

3.
Van DABC is AB = 20, BC = 24 en AC = 16.
De zwaartelijn uit het hoekpunt A snijdt de deellijn CE van LC in F.
Bereken de stukken CF en FE.

Zie figuur hieronder:
De aanpak is als volgt:
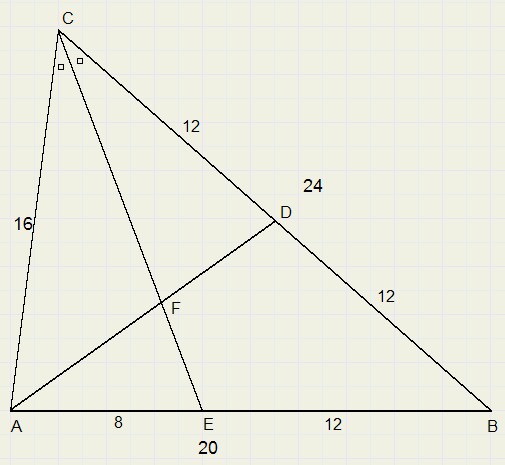
    - bereken AD met de stelling van Stewart
    - bereken de lijnstukken AF en FD met de deellijnstelling
    - bereken CF met de stelling van Stewart
    - bereken de lijnstukken AE en EB met de deellijnstelling
    - bereken CE met de stelling van Stewart
    - bereken FE = CE - CF
De stelling van Stewart zal ik in een apart artikel bewijzen, samen met enkele toepassingen.
De deellijnstelling luidt:
    De deellijn van een hoekpunt van een driehoek verdeelt de overstaande zijde in delen die zich verhouden
    als de lijnstukken om die hoek.
    Kijk [hier]

berekening van AD

Bekijk DABC. Stewart:
    24.AD2 = 12.AC2 + 12.AB2 - 12.12.BC
    AD2 = 184
    AD = 2 
    \46

berekening van AF en FD

bekijk DADC
Deellijnstelling............AF : FD = AC : DC = 4 : 3

Stel daarom AF = 4x en FD = 3x, zodat AD = 7x

7x = 2 
\46
 ............. x =
2
7
 
\46
AF =
8
7
 
\46
 .............. FD =
6
7
 
\46

berekening van CF

Stewart in DADC:

7x.CF2 = 3x.162 + 4x.122 - 3x.4x.7x
7.CF2 = 1344 - 84.x2
CF2 = 192 -
12.4.46
49
CF2 =
7200
49
 =
3600 · 2
49

CF =
60
7
 
\2

Berekening van AE en EB

bekijk DABC en pas deellijnstelling toe:

AE : EB = 16 : 24 = 2 : 3
stel AE = 2y................EB = 3y...................zodat................5y = 20..............y = 4
AE = 8, EB = 12

Berekening van CE

Stewart in DABC:

20.CE2 = 12.162 + 18.242 - 8.12.20
CE2 = 288 = 2.144
CE = 12 
\2

Berekening van FE

FE = 12 
\2
 -
60
7
 
\2
 =
24
7
 
\2

--- einde examen ---

Bewijs van de voetpuntsdriehoek

stelling:

De hoogtelijnen van een driehoek zijn de deellijnen van de voetpuntsdriehoek

Het bewijs maakt gebruik van gelijkvormigheid van driehoeken.
Daarom eerst in het kort wat theorie hierover.
Bekijk figuur 5. hieronder:
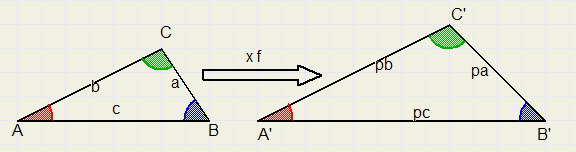    fig.5
DA'B'C' is een vergroting van DABC met een factor p.
Daarom noemen we de driehoeken gelijkvormig.
Bij vergroting blijven de hoeken gelijk.

Merk op, dat overeenkomstige zijden een gelijke verhouding bezitten:
    A'B' : A'C' = AB : AC............en bijvoorbeeld ook......................A'B' : AB = A'C' : AC
Om te bewijzen dat twee driehoeken gelijkvormig zijn volstaat
    1. aantonen dat ze gelijke hoeken hebben. {twee hoeken is uiteraard voldoende}
    of:
    2. aantonen dat de driehoeken 1 hoek gelijk hebben en hun zijden om die hoek een gelijke verhouding bezitten
Nu terug naar de stelling. Bekijk figuur 6.
    fig.6
AD, BE en CF zijn hoogtelijnen.
DDEF is de voetpuntsdriehoek.

wegens gelijke hoeken is................DBDA ~ DBFC.....................{let op juiste volgorde van letters}
zodat geldt
BD : AB = BF : BC

DDBF en DABC delen nu LB en hun zijden om LB hebben dezelfde verhouding.
Daarom is
DDBF ~ DABC..........zodat LBDF = LA

Wegens "symmetrie" of op eendere wijze als hiervoor is vast te stellen dat de gelijk gekleurde hoeken
in figuur 7 even groot zijn.
    fig.7
Hieruit volgt dat de hoogtelijnen in DABC de deellijnen zijn van DDEF