

 |
Twee handige Meetkunde Stellingen |  |
 |
Stelling 1
Als twee driehoeken een gelijke hoek hebben, dan verhouden hun oppervlakten zich
als het product van hun zijden om die hoek
Gegeven
DABC en DADE met gelijke LCABzie figuur 1.
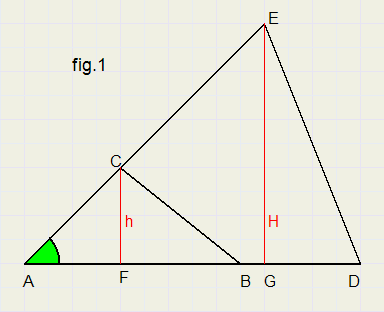
Opmerking: met [ABC] wordt bedoeld de oppervlakte van driehoek ABC
Te bewijzen:
-
[ABC] : [ADE] = (AB.AC) : (AD.AE)
Bewijs:
Trek hoogtelijnen CF en EG.CF = h en EG = H
[ABC] =
| h.A B |
| 2 |
[ADF] =
| h.A D |
| 2 |
| [A B C] |
| [A D E] |
| h.A B |
| H.A D |
maar DAFC ~ DAGE............zodat...........
| h |
| H |
| A C |
| A E |
| [A B C] |
| [A D E] |
| A C.A B |
| A E.A D |
Stelling 2.
In een driehoek verdeelt de deellijn van een hoek de overstaande zijde
in delen die zich verhouden als de zijden om die hoek.
Gegeven:
DABC met deellijn CDZie figuur 2.
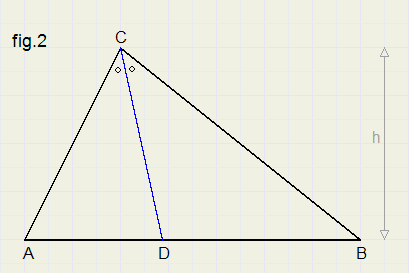
Te Bewijzen:
-
AC : BC = AD : BD
Bewijs
LACD = LDCB zodat we de hierboven bewezen stelling kunnen gebruiken.| [A D C] |
| [D B C] |
| A C.D C |
| B C.D C |
maar ook is natuurlijk
| [A D C] |
| [D B C] |
| h.A D |
| h.B D |
| A D |
| B D |
zodat
AD : BD = AC : BC

