prime number puzzle

A nice prime number puzzle

download program

download Delphi-7 project

Following prime number puzzle was placed on Facebook by mr. Andrey Dyukmedzhiev :

"What is the biggest prime number that can be formed by using digits 1..9 no more than once"

This article describes the approach and solution of this puzzle by writing a Delphi program.
This is the result:

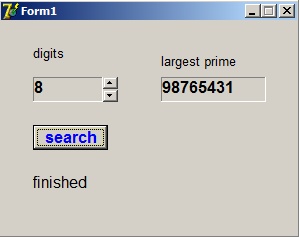
Note:
For the theory please refer to my article the basic theory of counting and coding

A number consisting of all digits 1..9 cannot be prime.
The sum of these digits is 45 which is divisible by 3 so any number
with digits 1..9 is also divisible by 3 and cannot be prime.
So our search starts by analysing 8 digit numbers.

I implemented a somewhat broader approach:
"search the biggest prime number consisting of k digits 1..9 choosen once" .

There are several ways to make selections of elements.
In this case the sequence is important because number 123 is different from 321
and also an element may be choosen just once.
Such a selection is called a variation.

How to solve this problem and write a (Delphi) program to have the computer do the work?
This project has 3 parts:

1. sequentially generate all numbers to be investigated for prime
2. test this number for being prime
3. systematically call 1. and 2. and report results

1.
A variation may be assigned a rank.
Thus, incrementing the rank makes all possible selections omitting none.
In case of k = 3 the rank ranges from 0 to 9*8*7 - 1 = 503.

The selection with rank 0 is 123, rank 1: 124....rank 503: 987.

How to translate a rank number to a digit selection?
Array elements originally holds elements 1..9.
Element[1] = 1...Element[9] = 9.
For the first choice there are 9 possibilities (out of 1..9) and the choice is (rank mod 9).
This produces a number digitnumber 0..8 so 1 must be added because we number our elements 1..9.
Now our digit = element[digitNr].

A selected element is removed (by shifting the next elements down) not to be selected again.
Rank = Rank div 9.

Next digitNr = (Rank mod 8) + 1 because the choice is out of 8 remaining elements.
Again digit = element[digitNr] and this element is removed by downshifting.
Rank = Rank div 8.

Next digitNr = (Rank mod 7) + 1.
Digit = element[digitNr]
and the three digits are choosen.

Finally these digits have to be multiplied by 1,10,100 to form the number
that will be tested for prime.

This Delphi function does the work:

function variation(rank : dword; k : byte) : dword;
//rank is sequence nr of variation of k digit selection 1..9
//result is made of choosen digits
var element : array[1..9] of byte;
    decexp : dword;//decimal exponent
    i,j,digit,digitnr : byte;
begin
 for i := 1 to 9 do element[i] := i;  //reset elements
 decexp := 1;
 result := 0;
 for i := 1 to k do
  begin
   digitnr := (rank mod (10-i)) + 1;
   rank := rank div (10-i);
   digit := element[digitnr];
   result := result + decexp*digit;
   for j := digitnr to 8 do element[j] := element[j+1];
   element[9] := 0;
   decexp := decexp*10;
  end;
end;

In schematic form:

2.
Testing a number for being prime.
Six successive numbers may be written as 6k, 6k+1,...,6k+5 where k=1,2,3,4.....
Only numbers that satisfy the expressions 6k+1 and 6k+5 may be prime.
6k is divisible by 2 and 3, 6k+2 is divisible by 2...etc.
So, we only have to examine type 6k+1 and 6k+5 numbers.

To test a number for prime is to test the absence of factors.
The number may not be a multiple of (smaller) prime factors.
The divisors are also limited to numbers satisfying the expression 6k-1 and 6k+1.
This is accomplished by incrementing the divisor alternately by 2,4,2,4...

Following function does the work:

function prime(Pnr : dword) : boolean;
//return true if Pnr is prime
//primes have format 6K-1 or 6K+1
var treshold : dword;
    divisor : dword;
    divincr : byte;
begin
 treshold := round(sqrt(Pnr));
 result := ((Pnr mod 3) > 0) and ((Pnr mod 5) > 0);
 divisor := 5;
 divincr := 2;
 while (result) and (divisor < treshold) do
  begin
   divisor := divisor + divincr;
   divincr := 6 - divincr;
   result := (Pnr mod divisor) > 0;
  end;
end;

Another trick to reduce processing time is limiting the divisor to
the square root of the number.
This is obvious because a*b = b*a : if Number / a = b then Number / b = a.
In case b > a the division Number / b adds nothing new.

3.
Calling above functions and showing results.

procedure TForm1.BitBtn1Click(Sender: TObject);
//search largest prime 
var i : byte;
    maxvar : dword;
    varnr : dword;
    N : dword;    
    oldprime : dword;
    digitcount : byte;
begin
 digitcount := updown1.Position;
 oldprime := 2;
 label3.Caption := 'searching';
 statictext2.Caption := 'no primes';
 application.ProcessMessages;
 maxvar := 1;
 for i := 1 to digitcount do maxvar := maxvar * (10-i);
 varnr := 0; //rank of variation
 repeat
  N := variation(varnr,digitcount);
  if ((N+1) mod 6 = 0) or ((N-1) mod 6 = 0) then
   if prime(N) then
    if N > oldPrime then
     begin
      oldPrime := N;
      statictext2.Caption := inttostr(N);
     end;
  inc(varnr);
 until varnr = maxvar;
 label3.Caption := 'finished'; 
end;

variables:

Controls: