Lissajous curves in motion

The graphics below are generated with Graphics Explorer, my equations grapher program.

download Graphics Explorer

Theory.

Lissajous was a French mathematician, who lived 1822 to 1880.
He is famous for his research on waves and oscillations.
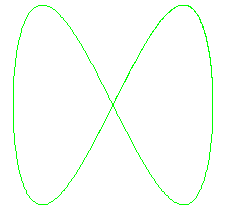
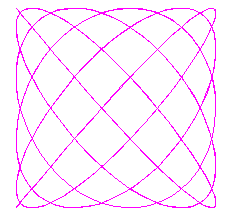
A particular kind of graphs are called "Lissajous curves",
3 examples are pictured right.

Lissajous curves are made by so called "parametric functions".

"common" functions, like y = 5sin(x) , produce a -single- y value for a value of x.
So, it is not possible to make graphs of spirals or even a circle, which needs 2 -y-
values for each value of x.

Parametric functions overcome this limitation by the following tric:
instead of y = f(x) we write:

y = g(v) and x = h(v)

so x and y are both functions of a new variable v.
(Graphics-Explorer uses v, often this variable is called t)

An example:
if y = 5sin(v) , x = 5cos(v) and v has domain 0..6.28 (2*p radians), the plotted curve
is a circle with centre (0,0) and a radius of 5.

In general:

a Lissajous curve is the graph of a parametric function
with both x and y being trigonometric functions of v

Molested Lissajous curves.

That's how we may call the picture right.
Lissajous curves, like common functions, will be smooth, without sharp angles.
The picture right is the result of the steps of v being too large.
This is how GraphicsExplorer paints parametric functions:

1.	stepvalue of v = (endvalue - startvalue)/number of steps
2.	calculate (x,y) coördinates using startvalue of v
3.	increment v by stepvalue
4.	calcalute next (x,y) and draw line to previous (x,y) coördinates
5.	repeat steps 3..5 until endvalue of v is reached

If the steps are too large, straight lines with angles instead of smooth curves will result.

Practice.

Start program Graphics-Explorer or goto [ Graphics-Explorer ] page first.
(download program by clicking on download (lightning) logo at top of page).
Select AUTOPLOT and REPLACE modes.
Type :

y = 5sin(v) ; x = 5cos(v)

and press ENTER.
Set start = 0 , end = 10 en steps = 100. Press ENTER

A circle with centre (0,0) and radius of 5 is plotted.

Erase graphics by menu:general:restart.
Type :

y = 5sin(a*v) ; x = 5cos(b*v)

Type ENTER or click PLOT button.
Move mousepointer over constants A and B and press (and hold) left or right mousebutton.
As the constants change, the function will be repaint, using the new values.
More accurate variations are obtained by decreasing the constants (+/-) increment value.
A higher number of steps for v will produce smoother curves.

Try this:

y = c*sin(a*v) ; x = c*cos(b*v)

Constant c is de size of the graphic.

Other Curves.

Interesting curves and artwork can be created by combining movements.
Type:

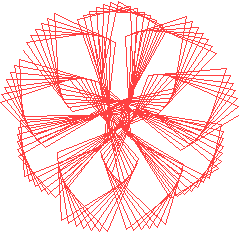
y = 5sin(a*v) + c*sin(b*v) ; x = 5cos(a*v) + c*cos(b*v)

A point rotates over a circle with radius = 5. The speed is a (radians/v).
This point is the centre of a circle with a radius of c.
The pen moves over this second circle with a speed of b.

Some examples:

y = 3sin(av)+csin(bv) ; x = 3cos(av) + ccos(bv)
start = 0 end = 10 steps = 200
A=8.4 B=96.41 C=3	A=13.81 B=42.1 C=3

Another example.
Type:

y = c*sin(a*v)(1 + sin(b*v)) ; x = c*cos(a*v)(1 + sin(b*v))

This represents a point moving over a circle with a speed of a (radians/v).
The radius of the circle is modulated by the factor (1 + sin(b*v)).

y = csin(av)(1 + sin(bv)) ; x = ccos(av)(1 + sin(bv))
start = 0 end = 10 steps = 200
A=30 B=11.88 C=3	A=100 B=25 C=3

Also, graphics of different formula's and colors can be combined.
Use menu:graphics:color to select other colors for background, grid or curves.

Success and have fun!

Note

Design artist Jennifer Townley builds machines that draw Lissajous curves.
Visit her website [HERE]