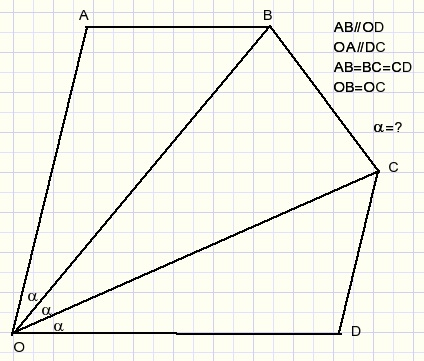
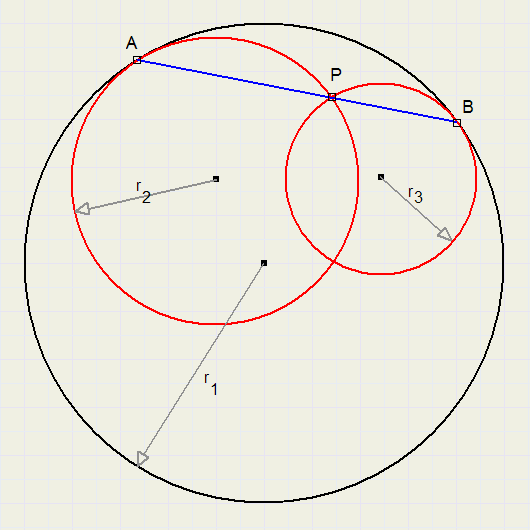
Geometry problems (1..10) problems 11..20 1. Given are: - a circle with radius r1 and inside - two circles with radius r2 and r3 which contact circle 1 at points A and B - the centers of circles 1,2 and 3. - the intersection point P of circles 2 and 3 Prove that: If P is on line AB then r1 = r2 + r3 must be true 2. In the figure above the circles have centers M, N. Proof, that the marked areas are equal. 3. 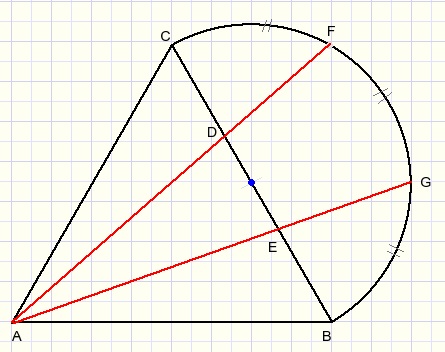Given are: Equilateral triangle ABC. M is the center of BC and also center of a circle arc through B and C. Arcs CF, FG and GB are equal in length. Prove that : CD = DE = EB. 4. Given is a square and a line CD = AB. Some angles (indicated by a small red square) are 300 Asked is the sum of angles a+b. 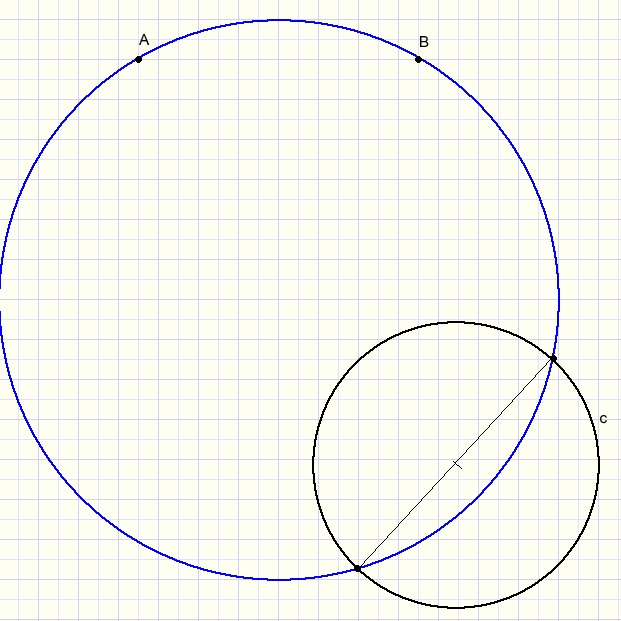5. Given are points A and B and a circle c. Construct a circle through A and B that intersects c in diametrically opposite points. 6. Given is square ABCD. Triangle CDP is equilateral. Calculate the size of LBAP. 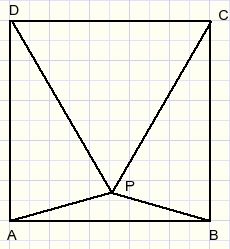7. 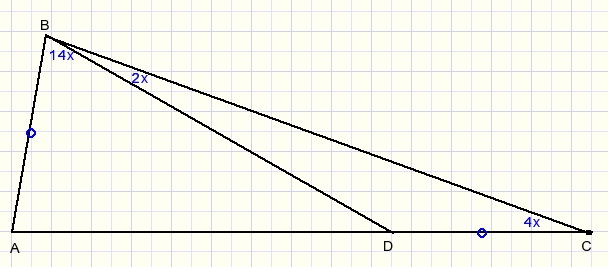Given are: 1. ΔABC with point D on BC such that AB=DC. 2. The relative size of some angles, see figure (in blue). Asked: find the value of x. 8. 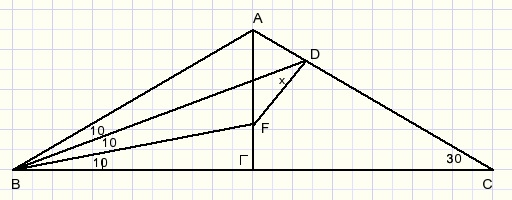Problem: calculate angle x in figure below: 9. 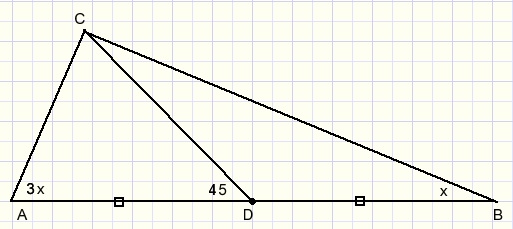AD=DB Question: prove that x=22.5 10.