

| geometry solutions 1..10 |
1.
Description
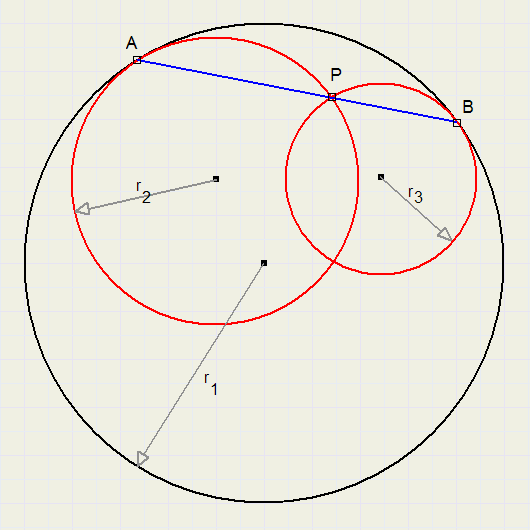
Given are:
- a circle with radius r1 and inside
- two circles with radius r2 and r3 which contact circle 1 at points A and B
- the centers of circles 1,2 and 3.
- the intersection point P of circles 2 and 3
Prove the following theorem:
-
If P is on line AB then r1 = r2 + r3 must be true
 |
Solution 1
(Bruce)
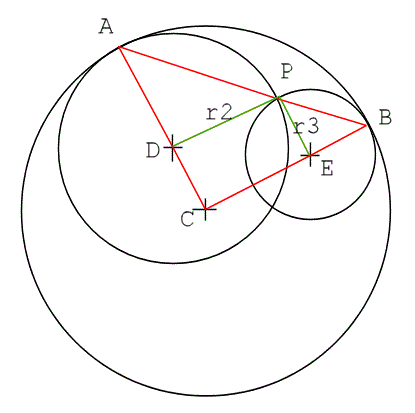
For APB to be a straight line, we need to show that the sum of angles
APD + DPE + EPB = 180
Notice that CD + AD = r1 also CE + EB = r1
But, our condition is r1 = r2 + r3
So, this means that DPEC is a parallelogram.
So, CD = r3 and CE = r2
Finally, we use the parallelogram to relate angles
DAP = EPB and ADP = DPE
Since angles of triangle ADP sum to 180deg
Then so do the angles on the line APB.
Solution 2
(Wim de Rijke)
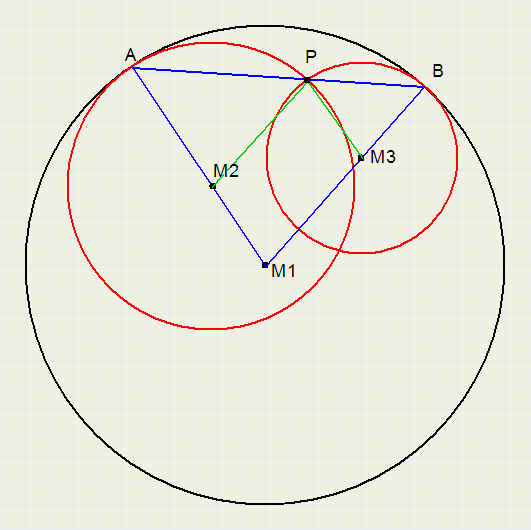
Call centers M1, M2 and M3.
Draw AM1, BM1.
AM1 and AM2 are on same line because perdendicular to tangent in A.
Same for BM1 and BM3.
Draw PM2, PM3.
Triangles APM2, BPM3 and ABM1 are isosceles and also equilateral because angles A, B are equal.
Equal angles at M1, M2 and M3 make M1M2PM3 a parallellogram.
M1M2 (= r1-r2) is equal to PM3 (=r3). So, r1 = r2+r3.
Solution 3
(myself)
Draw circle M4 with diagonal SC on AC. Angles at P, B, Q are 90 degrees (Thales).
PSQB is rectangle. AB and SQ are parallel.
Angles at A, S are equal.
Also, angles at A, P, B are equal because of isosceles triangles.
So, triangles PDB, SCQ are similar and because PB = SQ they are congruent.
Cirkel M3 is equal to M4.
2r1 = 2r2 + 2r3..........{diagonals}
r1 = r2 + r3
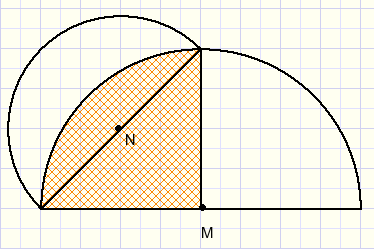
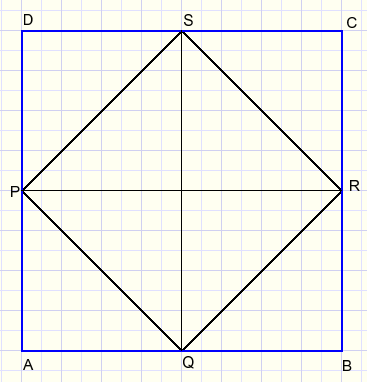
2.

In the figure above the circles have centers M, N.
Proof, that the marked areas are equal.
A first approach would be to define the radius of circle M = 1, than calculating the radius of circle N
using the Pythagoras lemma.
But a simplification is possible:
 |
 |
We also may proof, that the marked areas in above pictures are equal.
We do not need the Pythagoras lemma either.
In picture below we observe that area ABCD = 2* area PQRS.
Adding circles:
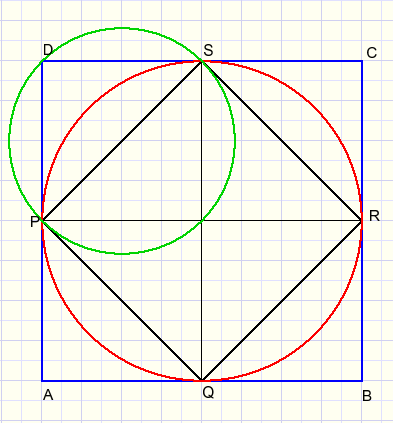
So, the large red circle has twice the area of the small green circle.
A quarter of the red circle equals half of the green circle.
That concludes the proof.
3.
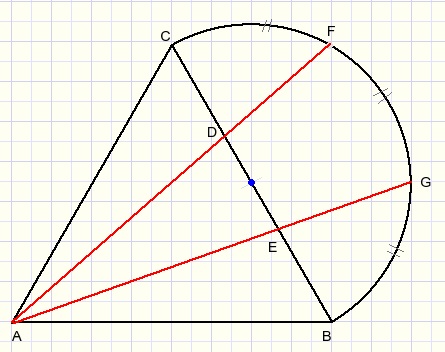
Given are:
Equilateral triangle ABC.
M is the center of BC and also center of a circle arc through B and C.
Arcs CF, FG and GB are equal in length.
Prove that :
CD = DE = EB.
Because of the symmetry: CD = EB.
Extend AB and FG, their intersection is H.
Draw lines FM, MG, GB.
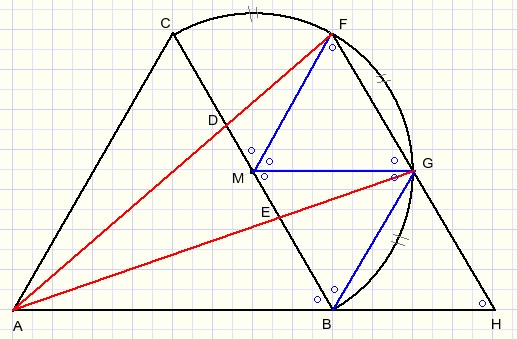
LFMG = 600.....one sixth of 3600
FM = GM, so LMFG = LMGF = 600
Similar:
LGMB=LMGB=LGBM=600.
LBGH=1800-600-600= 600
Conclusion:
FH||BC
Triangles FMG and BMG are equilateral and have a common edge MG.
Triangles BMG and BHG are equilateral and have a common edge BG.
So:
FG = GH.......(1)
Triangles ADE and AFG are similar so:
DE / FG = AE / AG .........(2)
Triangles AEB and AGH are similar so:
EB / GH = AE / AG .........(3)
Combining (2) and (3):
DE / FG = EB / GH now combine with (1):
DE = EB
4.
This geometry puzzle was brought to my attention by mr. Omid Motahed, math teacher in Beijing.

Given is a square and a line CD = AB.
Some angles (indicated by a small red square) are 300
Asked is the sum of angles a+b.
The first question is how to construct this figure.
The equal angles must span equal circle arcs (Thales lemmas).
So a good start would be to construct a circle through these angles using a radius of AB.
An equilateral triangle is attached to the squares edge opposite AB.
The top angle of this triangle is the center of the circle with radius AB.
The 300 angles span circle arcs of 600, which is part of a regular hexagon
dividing the circle in 6 equal arcs of 600.
Please refer to the grey lines in the picture before.
Asked is the calculation of angles a+b.
Knowing however that the exterior angle of a triangle is equal to the sum
of the opposite interior angles, we may restate the problem as:
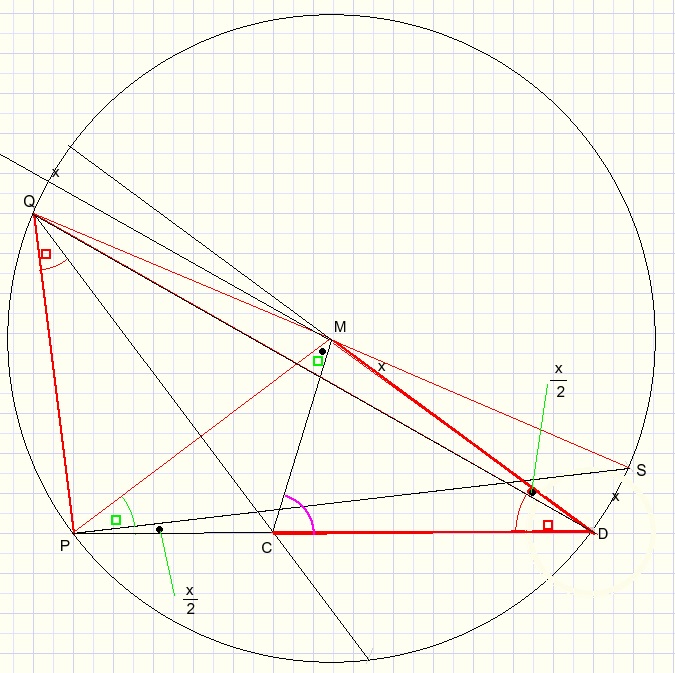
(a+b) = LSPD = x/2 after we call arc DS = x.
Now the problem is how to calculate arc x.
Have a look at LMCD.
This is the exterior angle of triangle PCM and also a base angle of isosceles triangle MCD.
LPQC=300...{given}
LQPS=900...{spans half of circle}
so
LMPS=90-60=300
2.LMCD + LCDM = 1800
LCDQ=300...{given}
Because of isosceles triangle MPC...{C on bisector of MP} :
the following equation emerges:
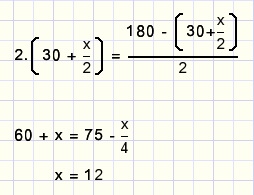
so (a+b) = 60
5.
This geometric construction problem was placed 14-09-2018 on facebook by Tungsteno.
The solution is my own.
Given are points A and B and a circle c.
Construct a circle through A and B that intersects c in diametrically opposite points.
In above picture, the blue circle is the solution.
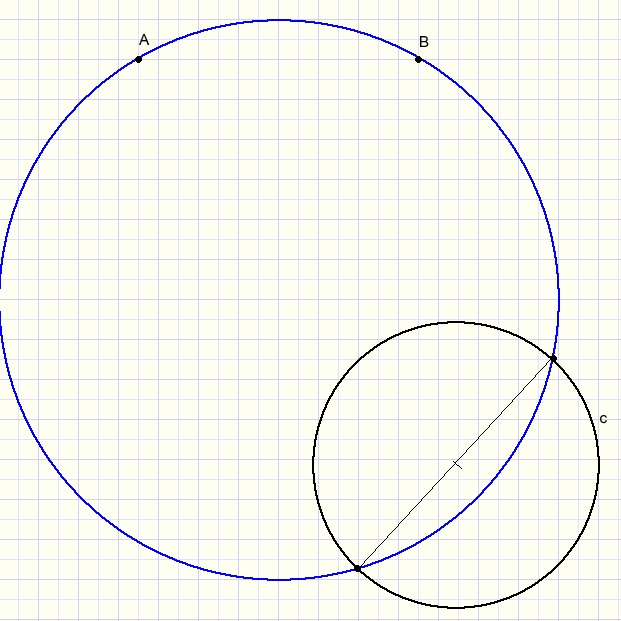
Now look at the picture below:

The center N of circle c we assume at distance 1 from line AB.
Center M of the circle we have to construct must be on the perpendicular bisector DF of AB.
N has distance b to this bisector.
So, 2x = BE2 - EP2.
We proceed:

Take E as center.
Circle EP.....EP'
Draw line from P' perpendicular to EN.
Circle EB , intersection with previous line is B'.
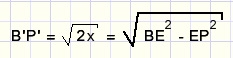
We have to square the above formula to obtain 2x.
Extend P'E such that P'Q = 1.
Draw P'T = P'B'
Draw TS parallel to QB'.
P'S = 2x
Note:

It looks like point S is on circle M.
Is this coincidence?
No, it is not.
Proof is left to the reader.
This concludes the construction.
An interesting problem.
However......
A nice thing about geometry is that logic reasoning may replace massive calculations.
In the previous solution only basic geometry rules were used together with some algebra.
In the next construction the algebra is absent because we use a powerfull lemma.
But first a proof.
Consider 1 point A and a circle.
Then many circles through A are possible that intersect the circle at diametrically opposite points (P and Q).
(just choose P and Q differently)
See picture below:
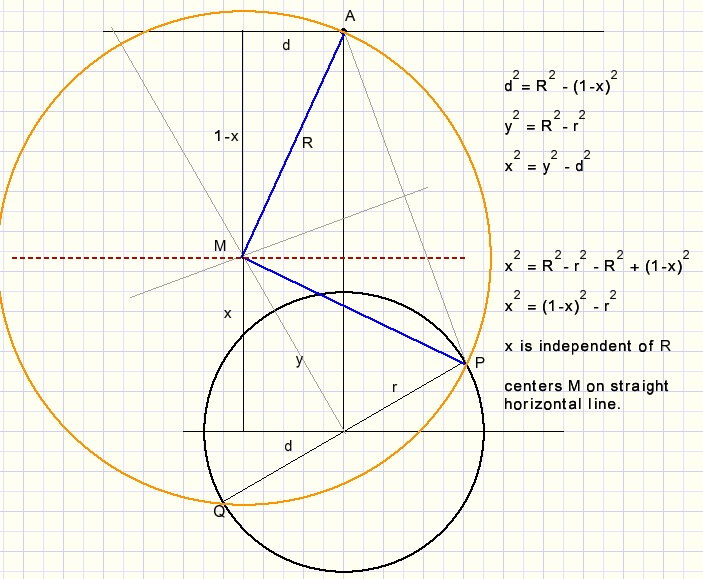
Here we assume that A has distance 1 to the circle center.
We notice that x is independent of radius R, so all centers M are on a straight horizontal line.
So, this is all algebra we need.
The new lemma is
-
If circles (M) through a point (A) intersect another circle (center N) in diametrically opposite points
than the centers (M) of these circles lay on a straight line
(perpendicular to AN)
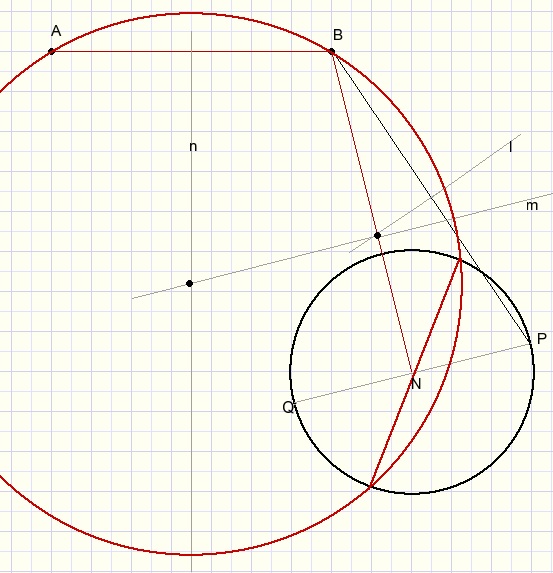
- draw BN.
- draw PQ perpendicular to BN.
- draw BP.
- draw line l, perpendicular bisector of BP.
- draw line m through intersection of l and BN parallel to PQ.
- draw line n, perpendicular bisector of AB
- center M of circle is intersection of m and n.
Note: possible circle centers are on line m.
But to run through point A, the center has to be on n as well.
6.
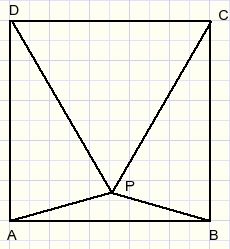
Given is square ABCD.
Triangle CDP is equilateral.
Calculate the size of LBAP.
This calculation is not difficult. The result is 150.
However, the reverse problem is not so easy:
Given is square ABCD and point P within such that LPAB = LPBA = 150.
Prove that triangle CDP is equilateral.
How to start such a proof?
The 150 angle does not bring us far.
We have to use the fact that ABCD is a square.
So let's start by reflecting ABP around diagonal AC.
Now look at the next picture, somewhat enlarged for clarity:
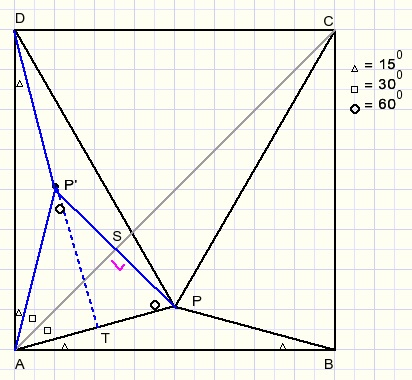
Point P' is the reflection of P on line AC.
Now focus on triangle APP'.
AP = AP' and LPAP' = 90 - 2*15 = 600.
LAPP'= (180 - 60)/2 = 600 so triangle APP' is equilateral.
We extend line DP' to point T on AP.
LATD = 180-15-15-60 = 900
P'T is perpendicular to AP and because triangle APP' is equilateral, T is the center of AP.
DT is the perpendicular bisector of AP.
So DA = DP.
For reasons of symmetry CP = DP.
Because ABCD is a square AD = CD.
Triangle CDP is equilateral.
7.
Following geometric problem was found on the Facebook group "Classical Mathematics".
Also a picture was provided showing the solution.
However, the steps leading to this solution were missing.
So the solution shown here is not mine but the steps are.
This is the problem:
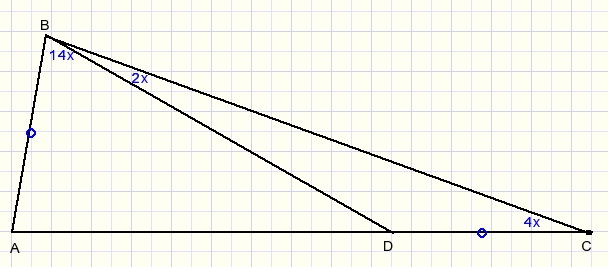
Given are:
1. ΔABC with point D on BC such that AB=DC.
2. The relative size of some angles, see figure (in blue).
Asked: find the value of x.
During this calculations we apply the lemma:
-
an exterior angle of a triangle is equal to the sum of the two interior opposite angles.
the calculations
Step 1.
Draw a circle with center D and radius DC.
P is the intersection of the circle with BC, so DP=DC and also LDPC=LPCD=4x.
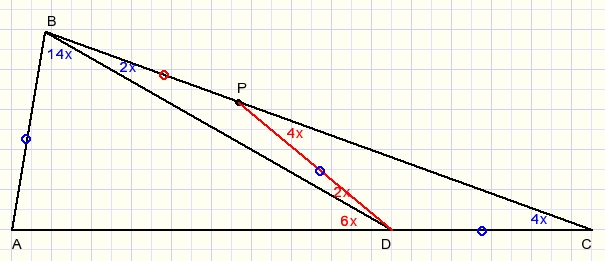
LADB=6x ... exterior angle of ΔBCD
LADP=8x ... exterior angle of ΔDCP
LBDP=8x-6x=2x
LPBD=LPDB so BP=DP and also AB=BP (=PD=DC)
Step 2.
Draw bisector BE of LABC.
Point E on AC.
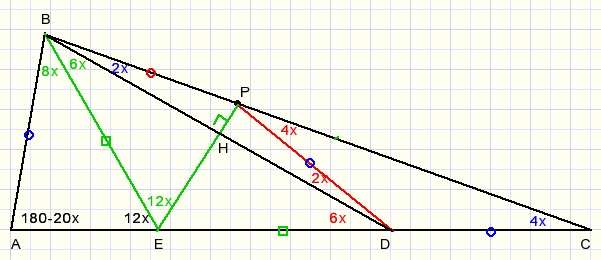
LAEB=12x ... exterior angle of ΔBEC
LAEB=LPEB=12x ... ΔBEA and ΔBEP are congruent.
LEBD=LBDE=6x so EB=ED
EP is perpendicular bisector of BD, all angles at point H are 900
Step 3.
LBEP=LDEP=12x ... ΔPEB and ΔPED are congruent.
Please look at point E:
36x=1800
x=5
A difficult problem.
8.
Problem: calculate angle x in figure below:
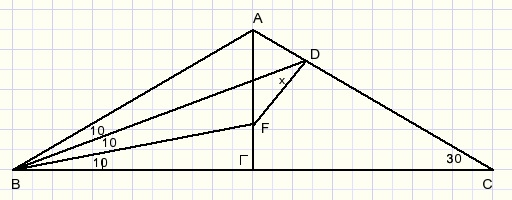
A great help is this lemma:
-
the exterior bisectors of two angles of a triangle and the bisector of the third angle intersect at one point.

Please look at the picture above:
M is the intersection of the bisectors of ΔABC.
N is the intersection of the bisectors of exterior angles B and C.
M and N are the centers of the inscribed and escribed circles.
Lines DM and FN are both perpendicular to AB.
LAMD=LANF.
So, AN is a straight line.
The solution
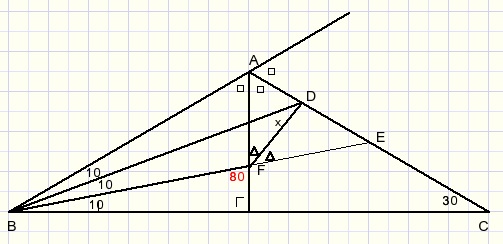
1. extend line BA
2. observe ΔABF
3. BD is interior bisector of B
3. AC is exterior bisector of A
4. D is the intersection of bisectors so, DF is exterior bisector of F
5. LAFE=800
6. LAFD=0,5*80=400
7. x+10 = 40
8. x = 300
9.
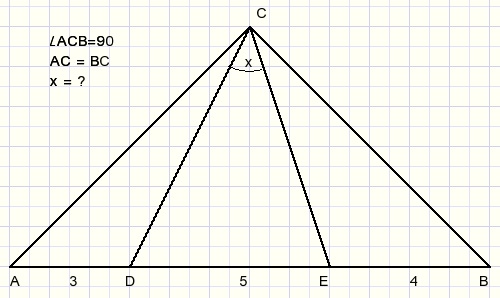
Above we see isosceles right angled triangle ABC.
Proof that angle x = LDCE = 45 degrees.
The lengths AD=3, DE=5 and EB=4 show a Pythagoras triple.
So we approach this problem in a more general way:
If AD=a, DE=c and EB=b and also a2 + b2 = c2
then prove that x = 45.
The proof
Shift lines AD and EB parallel to AB until they meet at point E.Because of similarity of ΔABC and ΔDEM (equal angles) MD = ME.
We prove that also MC = MD = ME.
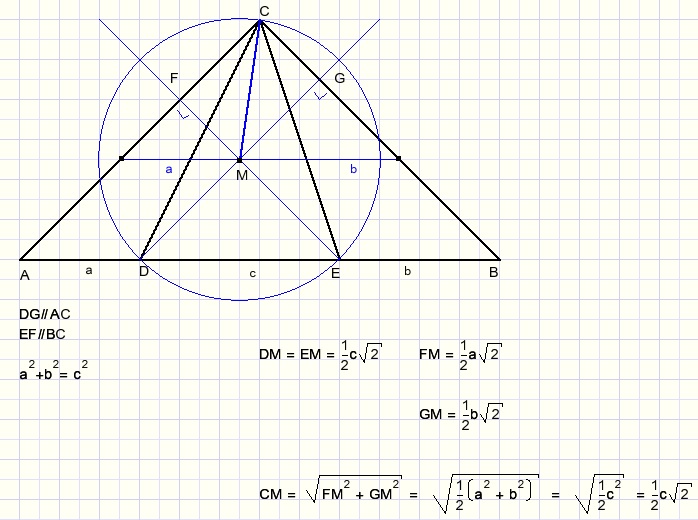
Note: in a right angled isosceles triangle with a hypothenuse of a, the other sides are
half the root of a.
M is the center of a circle through points D, E and C.
LDME spans arc DE of 90 degrees.
Angle x also spans arc DE so LDCE = 45.
10.
A geometry puzzle:
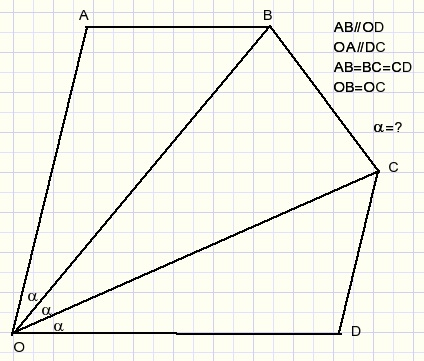
and the solution:
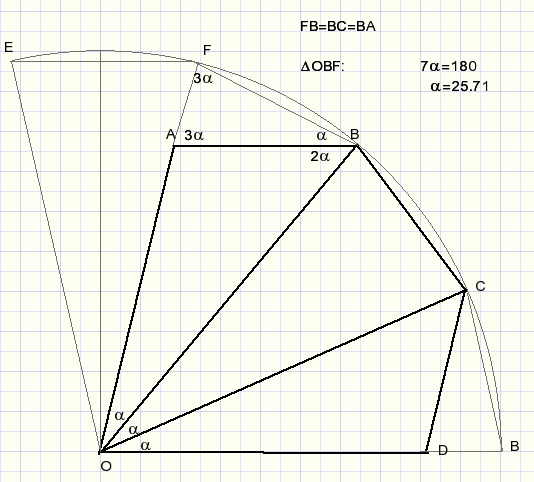
Explanation:
-
draw circle with center O and radius OB
LFAB = LFOD
LOBA = LBOD
LAFB = LBAF
LAFB = LOBF

