the flippo problem

the Flippo problem

Download (Windows) program

Download Delphi(7) project

Introduction

Flippo's are small cardboard or plastic discs with the printed image of a football player, movie star or comic hero.
In the '90s potato chips producer Smith added a flippo to their packets which made flippo collection a craze.

This is our problem:
After collecting a certain amount of flippos what is the chance to posses a complete series?
This article shows three methods of calculation.
Basic knowledge may be found at: a short course in combinatorics

A computer program is provided which provides for all calculation methods.

The flippos in a series I call 1,2,3,...,N
where N is the number of different flippos of the series.

The counting method

This method was developed first to serve as validation for later developed formulas.
We simply write rows of all possible series of K flippos possible and count
the rows that contain a complete series.

Say N=3 and K=5, then some of the 3⁵ = 234 rows are:

A "good" row is 3 3 1 1 2
A "wrong" row is : 2 2 1 1 2

For K flippos from a collection of N, N^K rows of K flippos are generated.
If G "good" rows are counted then the probability to posses a complete series in K flippos is:

This method is very time consuming so the limit is set to small numbers {N^K < 250.000.000}

A formula

This provides a fast and accurate calculation.
Say A(1) is the number of rows where flippo 1 is absent.
Such a row was generated by choosing K times from (N-1) flippos, so (N-1)^K rows result.
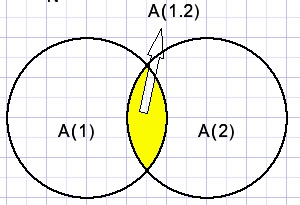
A(1+2) is the number of rows with missing flippos 1 OR 2 and
A(1.2) the number of rows with missing flippos 1 AND 2.
Read "+" as OR , "." as AND.
Then A(1+2) = A(1) + A(2) - A(1.2) the last term corrects for double counting.

Applying this rule further:
A(1+2+3) = A((1+2)+3) = A(1+2) + A(3) - A((1+2).3)
A((1+2).3) = A(1.3+2.3) = A(1.3) + A(2.3) - A(1.2.3)

These rules may be visualized by drawing overlapping areas as we noticed before.

Summing up :
A(1+2+3) = A(1) + A(2) + A(3) - [A(1.2 + A(1.3) + A(2.3)] + A(1.2.3)

A(1) = A(2) = ..= A(K) are N terms.
A(1.2) = A(1.3) = A(2.3) = .... = A((k-1),K) are just as much terms as we can select 2 flippos out of N.

This results in a formula for the amount of incomplete rows:

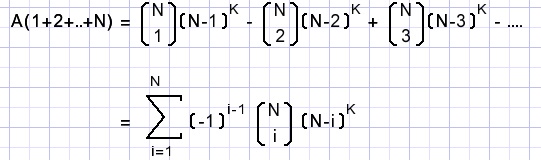
The number of "good" rows is N^K - A(1+2+..+N)
Division by N^K results in the probability for a complete flippo series in a collection of K.

A shorter formula

This formula provides an approximation which is only accurate for large numbers of K >> N

We choose a row of K flippos without flippo 1.
The probability for this row is:

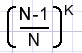
So, the probability for a row with at least 1 flippo -1- is:

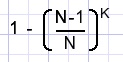
Repeating this formula for flippos -2..N- the probability of a complete series is:

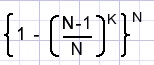
Above, we multiplied chances that were not completely independent which results in an error.
For large values of K however this error is small.
The formula may be simplified:

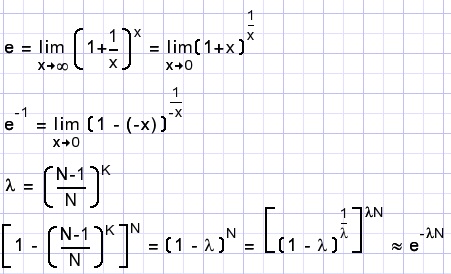
Table below shows some values for the case of N = 5
The "formula" column is accurate, the "e-power" column is calculated using the approximation method.

K	formula	e power
5	3,8%	19,4%
10	52,5%	58,5%
20	94,3%	94,4%

The program

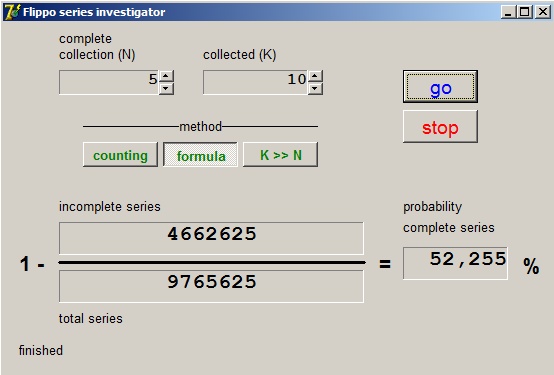
Download the program by clicking on the lightning icon, top left on this page.