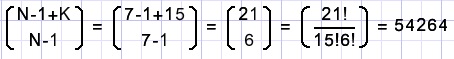| A short course in combinatorics |
Combinatorics is the part of math where possibilities are counted.
Examples are:
-
- the number of boards to choose from a group of people (chairman,secretary,cashier,members)
- the ways to connect railway cars (1st, 2nd class, luggage-, restaurant carriage)
- the number of sequences in which to visit 20 customers
- the number of ways to travel from A to B
1.Number systems
In the decimal system and using 6 digits we can make numbers from 000000 to 999999which are 106 = 1000000 rows of 6 digits.
In general, having N different digits, there are NK different numbers of K digits.
Example:
A 32-bit word in computer memory may hold 232 = 4294967296 numbers,
from 0 to 232 - 1 = 4294967295
Example:
Using characters A,B,D,E,F we can make 58 words of 8 characters,
from AAAAAAAA to FFFFFFFF.
2.Permutations
In the previous numbers any digit (element) could be choosen many times.In the case of visiting a number of customers once, each time the choice is from
the customers not yet visited.
Elements are choosen once.
N! = N(N-1)(N-2)....2.1 is called N faculty and is the way we can make sequences of N different elements.
N customers may be visited in N! sequences.
A sequence is also called a permutation.
The characters A,B,C,D can be arranged to make 4! = 4.3.2.1 = 24 words, from ABCD to DCBA.
Now follows an important rule.
How many sequences are possible if some elements are the same?
Let the elements be AAAABCDE.
The tric is making the A's different at first by applying an index:
A1A2A3A4BCDE are 8 elements which can make 8! sequences.
A1A2A3A4 are 4 elements which can make 4! sequences however
because they are the same only one sequence AAAA (4! times less) is possible.
So, 8! must be divided by 4! the answer is 8! / 4! = 8.7.6.5 = 1680 sequences.
Note: 0! = 1.
Example:
From 15 people a board is choosen (chairman,secretary,cashier).
Call the chairman A, secretary B, cashier C and call not choosen people N.
Then the number of boards possible is the way we can make sequences of ABCNNNNNNNNNNNN.
Applying the rule before: 15!/12! = 15.14.13 = 2730.
Example:
In how many ways can we arrange a train if there are 8 2nd class, 3 1st class, 3 luggage and 2 restaurant carriages?
Call first class F, second class S, luggage L and restaurant carriage R.
How many sequences are possible of the characters FFFSSSSSSSSLLLRR ?
16! must be divided by 8! (the second class) also by 3! (first class) 3! (luggage) and 2!(restaurants)
16!/(8!.3!.3!.2!) = 16.15.14.13.12.11.10.9/(6.6.2) = 7207200 possibilities.
3.Combinations
In case 1. elements (characters,digits) were reselectable and the sequence was important.In case 2. elements were not reselectable, but the sequence was important.
This case (3) is about selections in which elements are not reselectable and the sequence is unimportant.
Such a selection is called a combination.
Example:
After a party a team of 4 people (from a group of 12) must be selected to clean the area.
We apply the character Y to people selected and a N to not selected people.
The number of choices (combinations) is the possible number of sequences of characters YYYYNNNNNNNN
which is 12! divided by 4! and also by 8!.
12!/(4!.8!) = 12.11.10.9/(4.3.2.1) = 495.
Combinations are very common so a special notation exists:

Example:
A computer code exists of 3 zero bits and 4 one bits.
How many codes are possible?
Just the amount of codes as there are sequences of 0001111 which are the number of combinations
of 3 out of 7 = 7!/(3!4!) = 35.
Example: (Newton binomium)
(a+b)2 = aa + ab + ba + bb = a2 + 2ab + b2
(a+b)3 = aaa + aab + aba + abb + baa + bab + bba + bbb = a3 + 3a2 + 3ab2 + b3
We notice that a,b act as digits of a counter.
So, in (a+b)10 the term a7b3 originates from aaaaaaabbb and the number of occurrences
are the combinations of 7 out of 10.
The term has coefficient 10!/(7!.3!) = 120
Example:
below is shown a roadmap.
Question is how many roads exist from left top A to right bottom B.
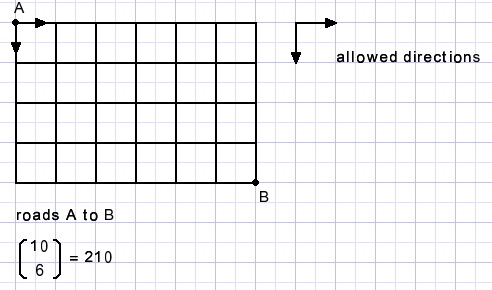
Call a horizontal direction H, vertical direction V, a possible road is HHHHHHVVVV
but all other combinations are fine.
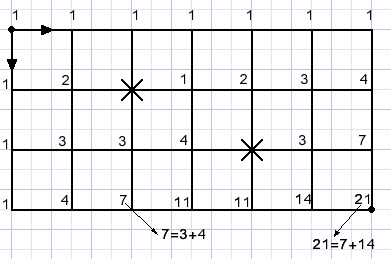
How to proceed is some roads are blocked?
Write a 1 at the starting position, we arrived here in one way.
For each road crossing, write the sum of the numbers of the preceding crossings.
4.Reselection without sequence
This is the case where digits may be (re)selected but the position is unimportant.In this case the number 54481 is equal to 14458.
I call this the zoo problem.
Say we want to built a zoo with 12 animals, the choice is of apes (A) bears (B) crocodiles (C) and eagles (E).
How many zoos are possible?
A possible zoo could be AAA | BBBB | CCC | EE
Call | a fence to separate the animals.
Then the number of zoos is the number of ways we can place the three fences:
AAAAAAA||CCCCC| would be a zoo with 7 apes, no bears, 5 crocodiles and no eagles.
Because the location of the animals is fixed, we no longer need the characters A,B,C and we write X.
The first zoo becomes: XXX | XXXX | XXX | XX.
Animals + fences + 12 + 3 = 15.
Three fences have to be placed where the choice is of 15 places.
Note that the number of fences is the number of different animals - 1.
The number of zoos are the combinations of 3 out of 15 so 15!/(12!3!) = 455.
Note: the selection is from XXXXXXXXXXXX--- where ---are the fences.
In general:
The number of K choices from N re-selectable objects where the sequence is unimportant is:
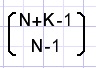
Example:
In how many ways can we paint 15 eggs if the choice is of 7 colors?
Comparing with the zoo problem:
Eggs = animal count, colors are animal types.
Align the egges and place cardboard between the colors.
K = 15 (eggs). N = 7 (colors).