 |
An integer cube root algorithm |  |
 |
A cube root algorithm
There are similarities with the square root algorithm. Please look [here].If number N = root3 + remainder, the cuberoot program returns the (cube) root and remainder of N.
 |
 |
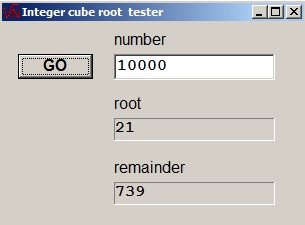Theory
Regard N as groups of 3 bits, counted from the right side.[ab]2 = 2a + b
(2a+b)3 = 8a3 + 12a2 + 6ab2 + b3.
At the start, a=0 and "1" is subtracted from rightmost bit in the highest group of N.
Then a=1, the term 8a3 = [1000]2 was subtracted from N.
Next bit b has to be found: 12a2b + 6ab2 + b3 must be subtracted from N.
If subtraction was possible, a becomes [a1]2 else a becomes [a0]2.
So, to find the next bit b requires trial substraction of 12a2b + 6ab2 + b3 from N
and because b=1 the substrahend becomes:
12a2 + 6a + 1 = [a0]([a0] + 1)*3 + 1.
Note: [a0]2 = 2a.
Each trial subtraction yields a new bit for the root.
For 30 bit numbers, these steps have to be repeated 10 times to generate a 10 bit result.
Note: Cube roots may be taken from negative numbers as well.
The program
function CubeRoot(N : longInt; var rem : longInt) : smallInt;
// -1,073,741,823 <= N <= 1,073,741,823
//return integer cube root of N and remainder rem
const max = 1073741824;
var NX,sub,r2 : longInt;
root : word;
p : shortInt;
neg : boolean;
begin
if (N <= -max) or (N >= max) then
begin
result := 0;
rem := N;
exit;
end;
if N < 0 then begin
N := -N;
neg := true;
end else neg := false;
p := 30;
root := 0;
repeat
r2 := root shl 1;
sub := r2*(r2+1)*3+1;
sub := sub shl p;
root := root shl 1;
NX := N - sub;
if NX >= 0 then
begin
N := NX;
root := root or 1;
end;
p := p - 3;
until p < 0;
if neg then begin
root := -root;
N := -N;
end;
result := root;
rem := N;
end;
procedure TForm1.GoBtnClick(Sender: TObject);
var N,rem : longInt;
root : smallInt;
begin
if length(numberEdit.Text) = 0 then numberEdit.Text := '0';
N := strtoInt(numberEdit.Text);
root := cubeRoot(N,rem);
rootLabel.Caption := inttostr(root);
remainderlabel.Caption := inttostr(rem);
end;
procedure TForm1.FormKeyPress(Sender: TObject; var Key: Char);
var OK,mt : boolean;
begin
OK := false;
with numberEdit do
begin
mt := length(text) = 0;
case key of
#8 : OK := true;
'1'..'9' : OK := true;
'0' : OK := not(mt);
'$' : OK := mt;
'a'..'f' : OK := text[1] = '$';
'-' : OK := mt;
end;
if OK = false then key := #0;
end;
end;
end.
download cube root program download cube root project
