An integer square root algorithm

Introduction

The Delphi programming language has operators div and mod for integer divide and remainder calculations.
For square root however only floating point calculations exist.
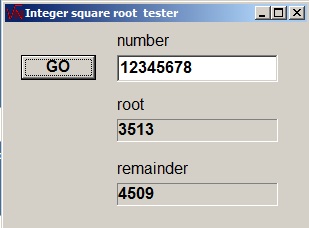
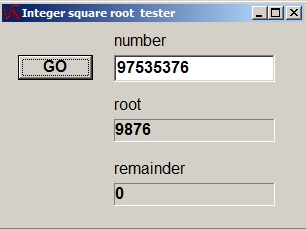
This project presents an integer square root algorithm which also supplies the remainder.

So we write for the square root of number N:
    N = root2 + remainder.
Please look at the pictures below:



The algorithm

The integer square root project uses 32bit positive integers (cardinal, dword) for N and
16 bit positive integers (word) as root and remainder.

For clarity an example is given where N is a byte.
We calculate the square root of 121 = $79 = [0111 1001]2.

First, the binary number N is organised as groups of 2 bits, counted from the right side.
Variables N, root and b are all bytes.

b is a single bit value (painted in red) and is initially positioned right in the leftmost group of 2 bits of N.
The variable root is zero initially (painted in black).
In the picture below, empty cells are zero.

The value root + b is subtracted from N only if N >= root + b.



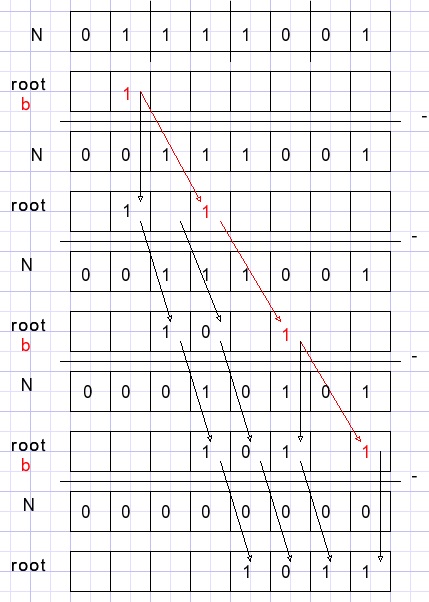
After a (trial)subtraction:
  • if subtraction took place, the b bit is copied to the root
  • the root is shifted one bit right
  • the b bit is shifted 2 bits right
This process continues until the b bit is shifted out of the byte.
Then N holds the remainder.

Why this works

Consider a binary number with 2 bits a,b : [ab]2 = 2a+b.
The square is (2a+b)2 = 4a2 + 4ab + b2
So this square is a four bit number.

Now, a2 = a, b2 = b for single bits.
for a = 1:
4a2=[100]2 and 4ab+b2=[101]2 if b=1.
If N >= [100] then [100] is subtracted from N and a=1
Remains to find the value of b.
For a=1 , 4ab + b2= [101] must be subtracted from N if b=1.
This applies to 4 bit numbers however:
These bits may be regarded as the 4 upper bits of a larger number.
After each (trial subtraction) step finding bit b, a is replaced by [ab]2.
Then a2 has already been subtracted from N so a next bit of b
has to be found by trial subtraction of [a01]2.

The program

N is the (32 bit) number from which the root is calculated.
At the end, N holds the remainder.
Variable root holds the value of a.
Variable b is b in the explanation before.
Initially, a is set to zero, b is set for the first subtraction to find a.
Then root holds the value of a.
Below is the procedure that calculates the integer root: 
function IntRoot(N : dword; var rem : word) : word;
//return integer square root of N and remainder rem
var b,root,sub : dword;
begin
 b := $40000000;
 root := 0;
 repeat
  sub := root or b;
  if sub <= N then
   begin
    N := N - sub;
    root := (root shr 1) or b;
   end else root := root shr 1;
  b := b shr 2;
 until b = 0;
 result := root;
 rem := N;
end;
procedure TForm1.GoBtnClick(Sender: TObject);
var N,root : dword;
    rem : word;
begin
 if length(numberEdit.Text) = 0 then numberEdit.Text := '0';
 N := strtoInt(numberEdit.Text);
 root := IntRoot(N,rem);
 rootLabel.Caption := inttostr(root);
 remainderlabel.Caption := inttostr(rem);
end;

procedure TForm1.FormKeyPress(Sender: TObject; var Key: Char);
var OK,mt : boolean;
begin
 OK := false;
 with numberEdit do
  begin
   mt := length(text) = 0;
   case key of
    #8       : OK := true;
    '1'..'9' : OK := true;
    '0'      : OK := not(mt);
    '$'      : OK := mt;
    'a'..'f' : OK := text[1] = '$';
   end;
   if OK = false then key := #0;
  end;
end;

 download root program

 download Delphi(7) project