A Bitmap Resize Algorithm
download
resize program		 download complete
Delphi-7 project		 read the BMresize
procedure code

Preface

The bitmap resize program has been replaced by a 5 to 10 times faster version.
The old program may still be found here.
The speed increase was realized by a faster pixel accesss method and optimized program code.

Introduction

Images in digital format consist of pixels, individual dots on a computer screen.
Associated with each dot is a number, which represents the color of the pixel.
Images in uncompressed form are stored as bitmaps (a *.bmp file) which is a two dimensional array of pixels.

Bitmaps may have several formats to represent pixel colors.
In this project I use the true color 32 bit format (pf32bit), see below.
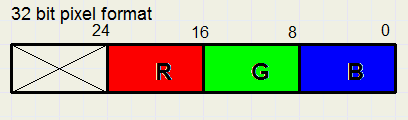
The three base colors (red,green,blue) have 8 bits each, so their intensity ranges from 0 to 255.

This is what a (very enlarged) pixel looks like:
Image below shows a bitmap with some coordinates.
A pixel is pictured as a square.

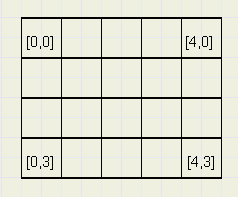
Above bitmap has 5 columns [0..4] and 4 rows [0..3].

The Algorithm

A source bitmap is copied to a destination bitmap having different dimensions.
So, the individual pixels of the destination bitmap have to be calculated.
This is done by scanning these pixels, left to right, top to bottom while projecting
the destination pixel over the source bitmap. See picture below:

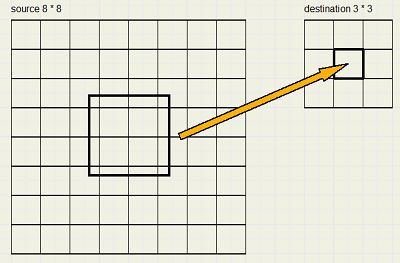
Bitmap dimensions and access

The source bitmap has columns 0..7 and also rows 0 .. 7.
The destination bitmaps has columns 0 .. 2 and also rows 0 .. 3.

Multiplication factor

The multiplication factor f = (source bitmap width) / (destination bitmap width).
In the picture above f = 8/3 = 2.6667
f > 1 means reduction, f < 1 means magnification.

We zoom in:
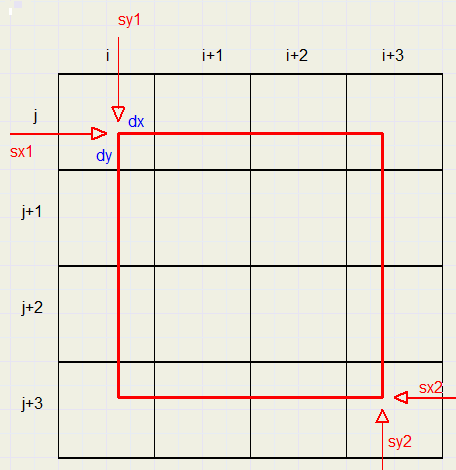
The red square is a pixel of the destination bitmap projected on the source bitmap.

The destination bitmap pixels are addressed by variables x and y.
[x,y] is a destination pixel at column x and row y.
The source bitmap columns and rows are addressed by variables i and j.
[i,j] is a pixel of the source bitmap at column i and row j.

We assume the width and height of a destination pixel is 1.
So, the red square has dimensions f * f, the multiplication factor.

sx1 is the left postion of the red square, sx1 = f * x.
Similar, sy1 = f * y is the top position.
sx2 = sx1 + f.
sy2 = sy1 + f.
Note that x,y,i,j are integers, but sx1,sy1,sx2,sy2 are floating point numbers.

dx * dy is the area of overlap of a source and destiantion pixel.
Note: dx and dy are floating point numbers as well.

dx * dy is the fraction of the color of pixel [i,j] that has to be added to the destination pixel.
What we have to do is
    1. read source pixel[i,j]
    2. extract the red, green and blue values
    3. multiply these values by dx*dy and adding them up per color
    4. repeat 1..3 for all overlapping pixels
    5. pack the summed red, green and blue colors in a dword (32 bit integer)
    6. store this dword in destination bitmap [x,y]
One other correction is necessary:
the summed colors are for an area size f*f, but their destination area is 1*1.
So, the summed colors from the source bitmap must be divided by f2.
Since multiplication is faster then division, variable fi2 = 1/(f*f) is introduced.

This describes the algorithm.
However, there is a pitfall.

Floating point accuracy

In this project, floating point numbers of type single are used which are 32 bits in size.
Accuracy is about 7 (decimal) digits, so a number like 1.5555555555 is rounded to 1.555556

Say, we reduce a 280*280 bitmap to 180*180.
f = 280 / 180 = 1.555556.
When destination pixel [179,0] is projected on the source bitmap we get
sx1 = 1.555556 * 179 = 278.4445 (rounded)
sx2 = 280.0001 (rounded)
Oops! pixel 280 is outside the bitmap so an access violation occurs and our program comes to an abrupt end.

What to do?
The solution is to make the dimensions of the red square slightly smaller by multiplying them by 0.9999
Edge length fstep = f * 0.9999 = 1.555400
Now, sx2 = 278.4445 + 1.555400 = 279.9999, nice within the bitmap.
Actually, we have corrected here for rounding errors.

Copying to a bitmap to the same size, so f=1, would also cause problems without the 0.9999 correction.
Say we copy a 100*100 bitmap.
For pixel 99 we get:
sx1 = 99
sx2 = 99 + 1 = 100, outside the bitmap.
Using 0.9999, sx2 = 99.9999, within the bitmap.

Calculations

i and j start, end values

In the example above, for destination pixel [x,y] the source pixels covered by the red square
have to be scanned. This is done by two loops:
1. an outer loop : for j := jstart to jend
2. an inner loop : for i := istart to iend

code: 
...
jstart := trunc(sy1);
jend := trunc(sy2);
istart := trunc(sx1);
iend := trunc(sx2);      
...
for j := jstart to jend do
....
  for i := istart to iend do
  ....

Width and Height independency

The source bitmap is bm1, the destination bitmap is bm2.
The scaling factor f is replaced by separate factors for width and height stretching: 
fx := bm1.width / bm2.width;
fy := bm1.height / bm2.height;
fxStep := 0.9999*fx;
fyStep := 0.9999*fy;
fix := 1/fx;
fiy := 1/fy;
...
sy1 := y*fy;
sy2 := sy1 + fyStep;
...
sx1 := x*fx;
sx2 := sx1 + fxStep;

dx and dy values

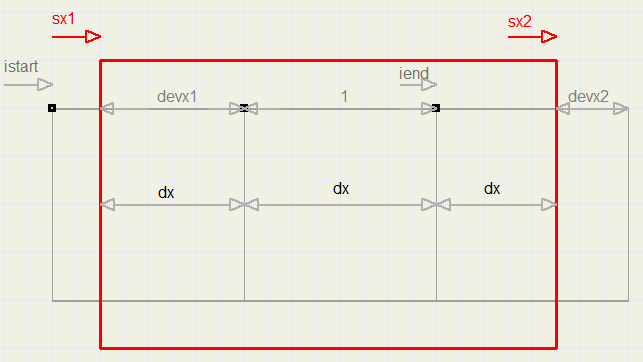
Calculations inside loops must be minimized.
dx has the choice of three values:
1. when i=istart, dx=devx1
2. when i=iend, dx=dx - devx2
3. else dx=1
Look at the picture below, where the red destination pixel is projected over the grey source pixels:
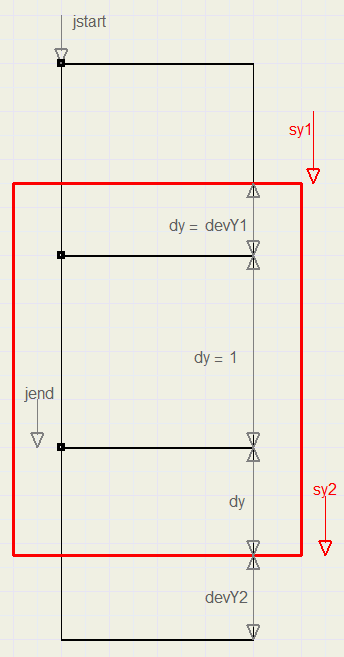
Note: istart and iend may be the same pixel, so dx is decreased when i=iend, presetting is not possible.

A similar scheme applies to dy.
1. when j=jstart , dy=devY1
2. when j=jend, dy = dy-devY2
3. else dy=1
See picture below

Loops

The resize procudure has an initializing part, followed by four embedded loops.
The outer loop is for y, addressing the destination bitmaps rows.
Within is the for x loop, addressing the destination bitmaps columns.
Within is the for j loop, addressing the source bitmaps rows.
And last within is the for i loop to address to source bitmaps columns.

For maximum speed, calcultions are best placed outside loops.
This is what happens.
Initializing
Calculate fx, fy, fix, fiy, fxStep, fyStep, destwidth, destheight

Inside for y := 0 to destheight do...........
Calculate sy1, sy2, jstart, jend, devY1, devY2.

Inside for x := 0 to destwidth do ...........
Calculate sx1, sx2, istart, iend, devX1, devX2.

Note: these values are recalculated for each y value.
Time may be saved to calculate them once and reload from a table.
However, code will get more complex.
The variables destR, destG,destB are the summing values for the [x,y] color.
They are reset to zero at this point.
dy is preset to devY1.

Inside for j := jstart to jend do ..............
Preset dx = devX1
Adjust dy if j = jend

Inside for i := istart to iend do ...............
Adjust dx if i = iend.
read color at [i,j] of source bitmap.
Extract sR, sG, sB individual RGB colors.
Calculate area factor AP = fix*fiy*dx*dy.
Add colors to destR, destG, destB:
destR := destR + sR*AP.......etc.

After i loop........
set dy = 1.

After j loop
round colors in destR, destG, destB
Pack colors in dword and store in destination bitmap [x,y]

Fast pixel access

The main speed increase is obtained by avoiding the slow TBitmap.pixels[ , ] and TBitmap.scanline[ ] properties.
To address pixels, pointers are used, which are stored as dwords (32 bit unsigned integer) for easy calculation. 
type PDW = ^dword
....
var ps0,pd0,psStep,pdStep : dword;
....
ps0 := dword(bm1.scanline[0]);
psStep := ps0 - dword(bm1.scanline[1]);
pd0 := dword(bm2.scanline[0]);
psStep := pd0 - dword(bm2.scanline[1]);
This is the only place scanline is used.
To read the pixel [i,j] of the source bitmap into color:
var p,color : dword;
....
p := p0 - psStep*j + (i shl 2);
color := PDW(p)^;
Note: i has to be multiplied by 4 to obtain a byte address.

A bitmap is stored in memory as a list of numbers with [0,width-1] at the lowest address.
In the pf32bit format, the psStep value = 4*(source width) and pdStep = 4*(destination width).

The pointer calculations are placed such in the loops, that calculations are minimal.
For details, please refer to the source code.

The complete project

Below is a reduced picture of the program at work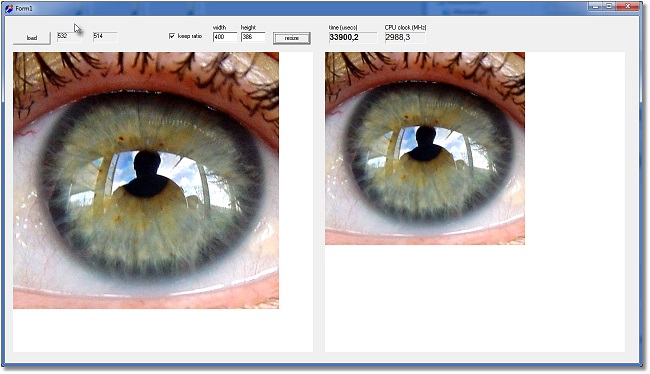
The project has one form (form1) and three units:
form1 :
paintboxes (600*600) to show the source and destination bitmaps.
buttons to load a *.bmp image and resize.
Edits for input of the new width, height dimensions.

unit1:
Handling of keyboard and mouse events.
paintbox painting, clock initialization.
Bitmap creation and destruction.

Resize unit:
Global bm1,bm2 source and destination bitmaps.
procedure BMresize.

TimerUnit:
A nanoseconds clock to measure resize performance.