

 |
a Bitmap Resize Algorithm |  |
 |
Announcement:
A 5 to 10 times faster version of this program has been completed.
This article and Delphi project will be replaced april 2015.
Introduction
Information can be stored in an analog or digital form.
The big advantage of digital storage is the possibility to manipulate the data using mathematical functions.
This article handles a simple algorithm to resize (enlarge or reduce) computer pictures.
Data formats and mathematics are discussed in detail.
The Delphi-implementation and full source-code listing are also included.
Data formats
A computer picture (or screen) is made up of dots which are called pixels.
A colored pixel is a mix of three colors: red, green and blue.
Using realistic colors, the intensity of each color is a number ranging 0..255.
0 means zero intensity, 255 (or hexadecimal ff) indicates the highest intensity.
This is what a (very enlarged) pixel looks like:
 |
Internally, Windows stores the data of each pixel in a 32 bit word:
 |
Bits 24..31 are not used.
A picture is a 2-dimensional table of pixels.
In Delphi, this table may be part of a Bitmap component.
This component offers the choice of several data formats and has procedures to manipulate
the pixels (drawing lines, filling areas, copying ...).
Bitmaps may be copied to a paintbox to be displayed on the screen.
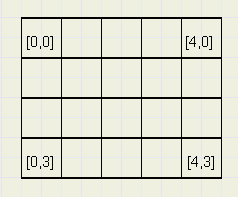
Pixeldata in the bitmap is addressed by using the [x,y] coordinates.
Image below shows a bitmap with some coordinates.
A pixel is pictured as a square.
 |
Commonly used pixelformats are: 16 bits, 24 bits or 32 bits.
24 bit is the Windows internal format.
In this application, the 32 bit format is used.
In this format, the colors red and blue have traded positions in the
32 bit word as compared to the windows format, so red is positioned
in bits 16..23 and blue in bits 0..7.
If a variable "color" has to receive the data of pixel[x,y] of a bitmap named bm1 then
-
color := bm1.canvas.pixels[x,y]
Notice, that "color" has the Windows format, regardless of the format in which
the colors were stored in the bitmap.
To further extract the individual color intensities into bytes R,G,B , use the statements:
-
R := color and $ff;
G := (color shr 8) and $ff;
B := (color shr 16) and $ff;
on form1 while positioning the left-top at paintbox position [x,y] , use the statement:
-
form1.paintbox1.canvas.draw(x,y,bm1)
Image below shows a source- and destination bitmap.
The source bitmap has 5 rows of 5 columns, the destination is a 4 * 4 bitmap.
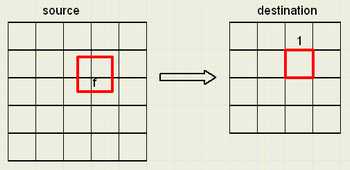 |
We regard the bitmaps as pieces of paper.
A pixel is given the dimension 1 * 1.
The destination bitmap dimensions are the dimensions of the source bitmap
divided by a factor f.
So, for each destination pixel, a corresponding area (f*f) on the source map may be drawn.
In most cases, this area will partially overlap the pixels in the source.
The color of a destination pixel is the (weighted) addition of the colors of
the pixels covered on the source map.
In the picture above, 4 pixels in the source contribute to the (marked) pixel
in the destination.
This contribution is proportional to the area covered.
We zoom into above picture to show the details:
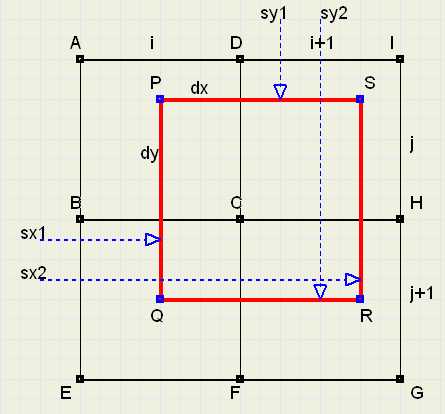 |
We see a part of the source bitmap with 4 pixels:
-
ABCD : [i,j]
DCHI : [i+1,j]
BEFC : [i,j+1]
CFGH : [i+1,j+1]
source bitmap. This projection is the (red) rectangle PQRS.
We must clearly distinguish pixel positions in the bitmap and distances on the map.
Pixel positions are [i,j] , so point A has distance i to the left and j to the top.
sx1,sx2,sy1,sy2 are variables of type single, which hold therefore floating point
values indicating the distance of the (red) square edges to the edges of the map.
Note , that PS = PQ = sx2-sx1 = sy2-sy1 = f;
If the destination-pixel is [x,y] then
-
sy1 := f * y;
sy2 := sy1 + f;
sx1 := f * x;
sx2 := sx1 + f;
j := floor(sy1);
i := floor(sx1);
fi2 := 1/(f * f);
Now, the colors of the pixel[i,j] must be extracted and the proper fraction
added to the destation colors
If dx,dy are the edges of the (red) rectangle overlapping pixel[i,j] then
-
dx := 1-(sx1-i);
dy := 1-(sy1-j);
PC := dx*dy*fi2;
color := bm1.canvas.pixels[i,j];
sR := color and $ff; //source red
sG := (color shr 8) and $ff; //source green
sB := (color shr 16) and $ff; //source blue
destR := destR + sR*PC; //dest red
destG := destG + sG*PC; //dest green
destB := destB + sB*PC; //dest blue
bm2.Canvas.pixels[x,y] := RGB(trunc(destR),trunc(destG),trunc(destB));//write destination
To calculate the color of destination-pixel [x,y], the above statements must be repeated
4 times, for all source pixels ABCD, DCHI, BEFC, CFGH.
This concludes the description of the algorithm.
For the reduction of a picture, a similar description holds.
Below is a picture of the form, showing the results
 |
Opendialog and Savedialog components are added to the form.
Two bitmaps are created: bm1 for the source, bm2 for the destination.
Paintbox1,2 components are used to display the bitmaps.
The overal procedure is:
-
- scan destination bitmap bm2 , row by row
- for each pixel in bm2, calculate overlap with source bitmap bm1
- scan all pixels in source which are overlapped
- add colors of these pixels according to fraction of overlap
- copy color to destination pixel
For larger images, the program is rather slow.
After the source listing, a modification is discussed to reduce processing time.
The complete source listing
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
StdCtrls, ExtCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
OpenDialog1: TOpenDialog;
PaintBox1: TPaintBox;
StaticText1: TStaticText;
StaticText2: TStaticText;
Label1: TLabel;
Label2: TLabel;
Edit1: TEdit;
Label3: TLabel;
Button2: TButton;
PaintBox2: TPaintBox;
SaveDialog1: TSaveDialog;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure FormKeyPress(Sender: TObject; var Key: Char);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.DFM}
var bm1,bm2 : TBitmap;
sw,sh : word;
procedure TForm1.Button1Click(Sender: TObject);
//load picture
begin
opendialog1.filter := 'bitmaps | *bmp' ;
if opendialog1.execute then
begin
bm1.loadfromfile(opendialog1.filename);
bm1.pixelformat := pf32bit; //in case other format loaded
end;
with paintbox1 do
with canvas do
begin
brush.color := 0;
fillrect(rect(0,0,width,height));
draw(0,0,bm1);
end;
sw := bm1.width;
sh := bm1.height;
statictext1.caption := inttostr(sw);
statictext2.caption := inttostr(sh);
end;
function floor(a : single) : word;
//return a rounded down to integer
begin
result := trunc(a);
end;
function ceiling(a : single) : word;
//return a rounded up to integer
begin
result := trunc(a);
if frac(a) > 0.0001 then inc(result);//fix acces violation if small fraction
end;
procedure TForm1.Button2Click(Sender: TObject);
//reduce or enlarge
var sx1,sy1,sx2,sy2 : single; //source field positions
x,y : word; //dest field pixels
destR,destG,destB : single; //destination colors
sR,sG,sB : byte; //source colors
destWidth, destheight : word;
f,fi2 : single;
i,j : word;
dx,dy,PC : single;
color : longInt;
begin
with paintbox2 do
with canvas do fillrect(rect(0,0,width,height));
//
destwidth := strtoint(edit1.text);
f := sw / destwidth;
fi2 := 1/f;
fi2 := fi2*fi2;
destheight := trunc(bm1.height/f);
with bm2 do
begin
width := destwidth;
height := destheight;
end;
//---
for y := 0 to destheight-1 do //vertical destination pixels
begin
sy1 := f * y;
sy2 := sy1 + f;
for x := 0 to destwidth-1 do //horizontal destination pixels
begin
sx1 := f * x;
sx2 := sx1 + f;
destR := 0; destG := 0; destB := 0; //clear colors
for j := floor(sy1) to ceiling(sy2)-1 do //vertical source pixels
begin
dy := 1;
if sy1 > j then begin
dy := dy-(sy1-j);
end;
if sy2 < j+1 then begin
dy := dy-(j+1-sy2);
end;
for i := floor(sx1) to ceiling(sx2)-1 do //horizontal source pixels
begin
dx := 1;
if sx1 > i then begin
dx := dx-(sx1-i);
end;
if sx2 < i+1 then begin
dx := dx-(i+1-sx2);
end;
color := bm1.canvas.pixels[i,j];
sR := color and $ff;
sG := (color shr 8) and $ff;
sB := (color shr 16) and $ff;
PC := dx*dy*fi2;
destR := destR + sR*PC;
destG := destG + sG*PC;
destB := destB + sB*PC;
end;//for i
end;//for j
bm2.Canvas.pixels[x,y] := RGB(trunc(destR),trunc(destG),trunc(destB));
end;//for x
end;//for y
paintbox2.canvas.draw(0,0,bm2);
end;
procedure TForm1.FormKeyPress(Sender: TObject; var Key: Char);
//make picture for website
var formImage : Tbitmap;
begin
if upcase(key) = 'P' then
begin
formimage := Tbitmap.create;
formimage := getformimage;
formImage.canvas.draw(paintbox1.left,paintbox1.top,bm1);
formImage.canvas.draw(paintbox2.left,paintbox2.top,bm2);
if savedialog1.execute then
formImage.savetofile(savedialog1.filename);
formImage.free;
end;
end;
initialization
bm1 := Tbitmap.create;
with bm1 do
begin
pixelformat := pf32bit;
width := 100; height := 100;
end;
bm2 := TBitmap.create;
with bm2 do
begin
pixelformat := pf32bit;
width := 100; height := 100;
end;
sw := 100; sh := 100;
finalization
bm1.free;
bm2.free;
end.
Speeding upThe following procedure is slow:
-
color := bm1.canvas.pixels[i,j]
To bypass windows and directly address the pixels in the array, a pointer is used.
This pointer is the scanline property of the bitmap component.
If p is a pointer to a large a9one dimensional) array of LongInt and
-
p := bm1.scanline[y]
-
color := p^[x]
Below is the modified procedure.
procedure TForm1.Button2Click(Sender: TObject);
//reduce or enlarge
type TWa = array[0..1000] of longInt;
PWa = ^TWa;
var sx1,sy1,sx2,sy2 : single; //source field positions
py,pj : PWa;
x,y,i,j : word; //source,dest field pixels
destR,destG,destB : single; //destination colors
sR,sG,sB : byte; //source colors
destWidth, destheight : word;
f,fi2 : single; //factors
dx,dy,AP : single; //distance, area percentage
color : DWord;//longInt;
begin
with paintbox2 do
with canvas do fillrect(rect(0,0,width,height));
//
destwidth := strtoint(edit1.text);
f := sw / destwidth;
fi2 := 1/f;
fi2 := fi2*fi2;
destheight := trunc(bm1.height/f);
with bm2 do
begin
width := destwidth;
height := destheight;
end;
//---
for y := 0 to destheight-1 do //vertical destination pixels
begin
sy1 := f * y;
sy2 := sy1 + f;
py := bm2.ScanLine[y];
for x := 0 to destwidth-1 do //horizontal destination pixels
begin
sx1 := f * x;
sx2 := sx1 + f;
destR := 0; destG := 0; destB := 0; //clear colors
for j := floor(sy1) to ceiling(sy2)-1 do //vertical source pixels
begin
pj := bm1.scanline[j];
dy := 1;
if sy1 > j then begin
dy := dy-(sy1-j);
end;
if sy2 < j+1 then begin
dy := dy-(j+1-sy2);
end;
for i := floor(sx1) to ceiling(sx2)-1 do //horizontal source pixels
begin
dx := 1;
if sx1 > i then begin
dx := dx-(sx1-i);
end;
if sx2 < i+1 then begin
dx := dx-(i+1-sx2);
end;
color := pj^[i];
sB := color and $ff;
sG := (color shr 8) and $ff;
sR := (color shr 16) and $ff;
AP := dx*dy*fi2;
destR := destR + sR*AP;
destG := destG + sG*AP;
destB := destB + sB*AP;
end;//for i
end;//for j
color := trunc(destB);
color := color or (trunc(destG) shl 8);
color := color or (trunc(destR) shl 16);
py^[x] := color;
end;//for x
end;//for y
paintbox2.canvas.draw(0,0,bm2);
end;


