| Magische vierkanten (vervolg) |  |
Ook hier laten we eerst de eis van verschillende cijfers per veld even vallen.
Alleen unieke cijfers per rij, kolom en diagonaal.
Dan moeten de 4 middelste velden 0,1,2,3 zijn, want die maken deel uit van zowel een rij,
een kolom en een diagonaal.
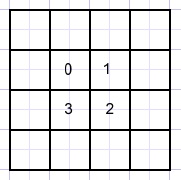
Omdat er veel symmetrieŽn zijn maakt het volgende cijfer niets uit zolang de som maar 0+1+2+3=6 bedraagt.
De 2*2 vierkantjes (links en rechts, boven en onder) moeten 0,1,2,3 in hun velden hebben
omdat er een diagonaal doorheen gaat.
De andere cijfers staan nu vast. We zien dat veel dezelfde cijfers een paardensprong afstand hebben.
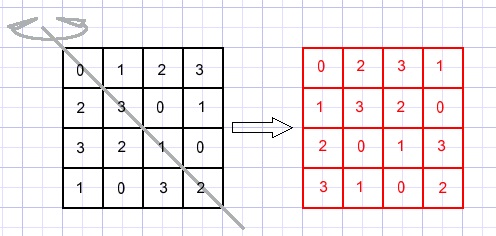
Spiegelen om de vertikale lijn door het midden werkt hier niet omdat na samenvoeging
geen unieke getallen ontstaan.
We proberen spiegeling om de diagonaal links boven - rechts onder.
Nu de velden samenvoegen, van 4 naar 10 tallig stelsel en bij elk veld 1 bijtellen.
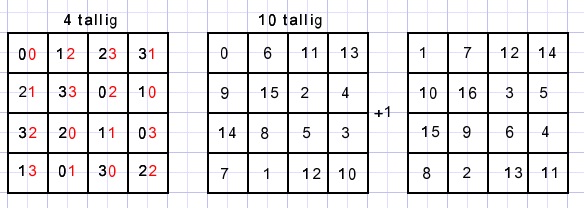
En ziedaar.
Merk op, dat elk viertal (2*2) velden waar een diagonaal doorheen gaat opgeteld ook 34 maken.
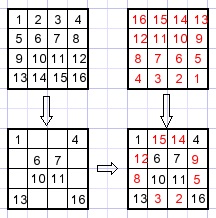
Er bestaat een truuk om snel magische vierkanten te maken die een veelvoud van 4 zijn.
Schrijf in zo'n vierkant de getallen 1,2,3.. in normale volgorde.
Schrijf deze getallen ook in een ander vierkant, maar dan in omgekeerde volgorde.
Laat in elk 4*4 vierkant de middelste getallen van elke zijde weg.
Vul nu op deze lege velden het getal uit de omgekeerde tabel in.